有向图的强连通分量算法

有向图的强连通分量算法

1. 强连通分量定义
   在有向图中，某个子集中的顶点可以直接或者间接互相可达，那么这个子集就是此有向图的一个强连通分量，值得注意的是，一旦某个节点划分为特定的强连通分量后，此顶点不能在其它子树中重复使用，隐含了图的遍历过程和极大化原则。
   让我们用下图为例进行说明强连通分量含义：
   
   上面有向图中，包含四个强连通分量，每个强连通分量中都包含一个或多个连通路径，如果去掉其中任意顶点，那么其互相可达的性质就会被破坏。值得一提的是，遍历完成后，剩余的单个顶点本身也是强连通分量，如图中橙色所示。

2. 如何求解某个图的强连通分量
   求解强连通分量的过程为施加条件的遍历过程，一般需要使用深度优先遍历过程。过程中需要屏蔽 不同强连通分量之间的互相干涉，根据屏蔽过程不同，一般分为两类算法：

• Tarjan 算法，通过记录DFS对每个顶点先序遍历的时间戳，一般用disc[]数组表示，实现对访问次序的跟踪；然后引入low[]数组，记录从当前访问顶点 所能到达的最小（最低)顶点序列号；最后引入栈，来屏蔽不同强连通分量之间的互相干涉；
• Kosaraju 算法，其本质为连个DFS遍历。第一个DFS针对原始图进行操作，第二个DFS针对边逆向的图进行操作，可以选择十字链表或邻接表的储存结构，通过逆向图，做到了不同强连通分量之间的互相屏蔽

3. 算法分析
   3.1 Tarjan 算法
   a) Low 数组
   正式进入Tarjan算法之前，需要对low[]数组概念深入理解。low[]数组记录遍历过程中，当前顶点所能到达的最小的顶点序列号。如果当前顶点及其子树没有back edge, 那么low[]的值就是当前DFS访问的时间戳号；如果当前顶点或其子树存在back edge就需要在每个邻接点的递归退出后进行比较。
   让我们用示意图进行说明，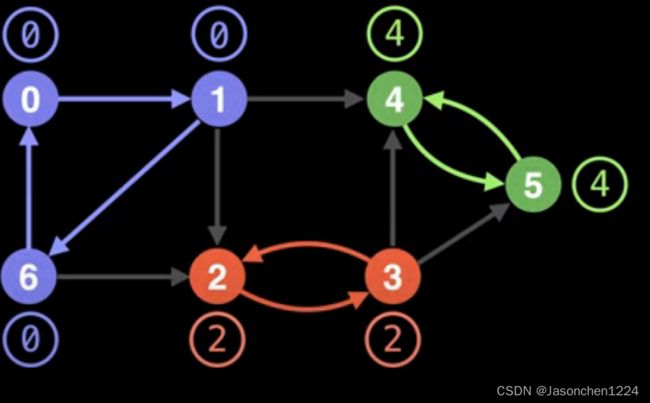
   DFS 以为0，1…6的次序进行遍历，边上带圆圈的值就是各个顶点的low[]具体值。我们以紫色的强连通分量为例，当遍历至顶点#6之前，1号顶点的low[1]=1;当遍历#6顶点后，需要比较#6和#0的low值，取最小值，作为#6顶点的low值，也即low[6]=min{low[0],low[6]}=0；可能大家有疑问，为什么不用#6顶点的low值和#2顶点比较呢？ 这个问题其实涉及到下一个话题，暂且不表。然后继续回退low[1]=min{low[6],low[1]}=0，最后回到起始点low[0]={low[1],low[0]}=0.

如果起点选择适当，那么结合下一个栈话题，就可以求得图的所有连通分量。

上图的遍历方式从左边开始，最后完成强连通分量的求解。
那么如果从最右边的顶点开始，求解强连通分量，会有什么状况发生呢？

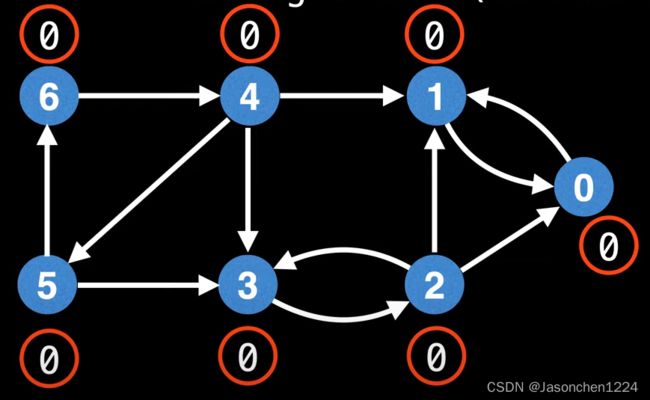
此时所有的low值均为0，显然不符合实际情况。那么就需要引入栈，对所有顶点进行出栈管理，避免不同强连通分量之间互相干扰。
b) 栈的作用
通过引入栈，可以有效客服随机顶点访问带来的问题，Tarjan算法通过维护栈，只有在栈里面的顶点才有机会更新low值。顶点在第一次DFS遍历的时候入栈，当找到一个完整的强连通分量，顶点出栈。那么何时出栈呢？ 遍历回退，而且disc[u]==low[u]的时候，便表示整个最大的强连通分量环已经找到，便可以出栈直到u出栈。

c) Tarjan算法代码实现

//ALGraph is Adjacent list graph
//Vertex Type is the vertex name, it is char type
void find_scc(ALGraph G, void (*visit)(VertexType e))
{

    int i;
    int u;
    int disc[MAX_VERTEX_NUM];
    int low[MAX_VERTEX_NUM];
    bool stk_status[MAX_VERTEX_NUM];
    SqStack stk; //Stack definition by C language, you can define it

    InitStack_Sq(&stk);

	//Initialize disc, 
    for(i=0;i<G.vexnum;i++)
    {
        disc[i]=-1;
        low[i]=-1;
        stk_status[i]=false;
    }

    for(u=0;u<G.vexnum;u++)
    {
        if(disc[u]==-1)
        {
            find_component(G,u,disc,low,&stk,stk_status,visit);
        }
    }
}

void find_component(ALGraph G, int u, int *disc, int *low, SqStack *stk, bool *stk_status, void (*visit)(VertexType e))
{
    
    static int time =0; //time stamp, visiting sequence by DFS
    int popped_item;
    int v;
    int w;
    *(disc+u)=low[u]=++time;
    Push_Sq(stk,u); //Push u into the stack
    *(stk_status+u)=true; // Follow whether u is in the stack   
	
	//FirstAdjvex and NextAdjVex function, reference to 
	//<>, TsingHua University,YanWenMin
    for(w=FirstAdjVex(G,u);w>=0;w=NextAdjVex(G,u,w))
    {
        if(disc[w]==-1)
        {
            find_component(G,w,disc,low,stk,stk_status,visit);
            low[u]=minimum(low[u],low[w]);
        }
        else if(stk_status[w])
        {
            low[u]=minimum(low[u],disc[w]); //back edge in the graph
        }
    }

    popped_item=0;
    if(low[u]==disc[u])
    {
        GetTop_Sq(*stk,&popped_item); // Get top element from stack
        while(popped_item!=u)
        {
            visit(G.vertices[popped_item].data);
            stk_status[popped_item]=false;
            Pop_Sq(stk,&popped_item); //Pop element from stack
            GetTop_Sq(*stk, &popped_item);
        }

        visit(G.vertices[popped_item].data);
        stk_status[popped_item] = false;
        Pop_Sq(stk, &popped_item);
        printf("\n");
    }
}

int minimum(int a, int b)
{
    return (a>b?b:a);
}

3.2 Kosaraju 算法
Kosaraju 算法本质是两个深度优先遍历，但是遍历的对象略有不同，初始遍历对象为原始连接图，第二次遍历对象为边反转图。第一次遍历过程中，在退出递归过程中，需要用栈或数组保存退出过程中的序列号，用作第二次遍历的基本顺序。
所以总结起来分为三步:
I) 对原始图进行DFS遍历，退出遍历前，用栈保存遍历的序号
II) 对原来的Graph进行反转操作，如果是十字链表的储存图，此步可以省略
III)在反转图上进行DFS遍历，求解出有向图的强连通分量
让我们用图形进行解释，

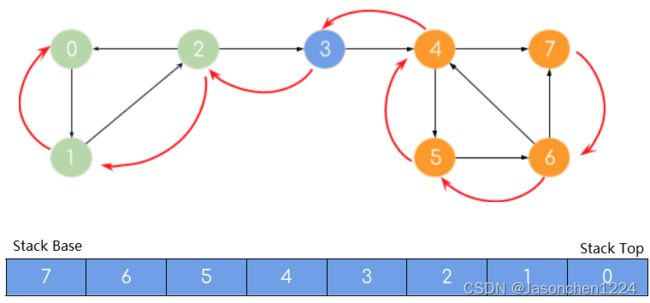
上图从0开始遍历，#7顶点结束；在退出遍历时候进行入栈操作，栈顶和栈底如上图所示。红色线条表示回退过程。

然后利用程序，对图进行反转操作（黑色箭头），反转后用红色直线箭头表示，如下图所示：

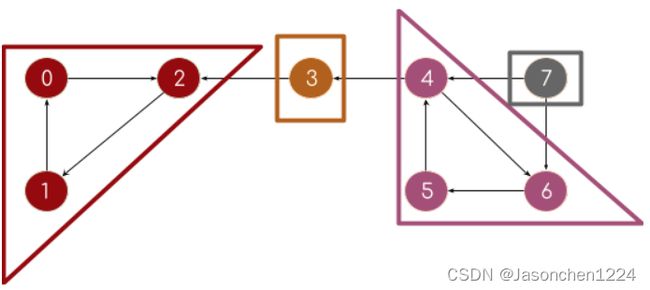
最后对反转图进行DFS遍历，求得强连通分量。

Kosaraju 代码

void DFS_traverse_original(ALGraph G, SqStack *stk)
{
    int i;
    int u;

    for(i=0;i<G.vexnum;i++)
    {
        visited[i]=0;
    }

    for(u=0;u<G.vexnum;u++)
    {
        if(!visited[u])
        {
            DFS_original(G,u,stk);
        }
    }
}

void DFS_original(ALGraph G, int u, SqStack *stk)
{
    int v;
    int w;

    visited[u]=1;

    for(w=FirstAdjVex(G,u);w>=0;w=NextAdjVex(G,u,w))
    {
        if(!visited[w])
        {
            DFS_original(G,w,stk);
        }
    }

    Push_Sq(stk,u); //Here is the best part of this algorithm
}

void DFS_traverse_transpose(ALGraph Rev_G, SqStack *stk, void (*visit)(VertexType e))
{
    int i;
    int u;

    for(i=0;i<Rev_G.vexnum;i++)
    {
        visited[i]=0;
    }

    while(!StackEmpty_Sq(*stk))
    {
        Pop_Sq(stk,&u);

        if(!visited[u])
        {
            DFS_transpose(Rev_G,u,visit);
            printf("\n----------\n");
        }
    }
}

void DFS_transpose(ALGraph Rev_G, int u, void (*visit)(VertexType e))
{
    int w;
    
    visited[u]=1;
    visit(Rev_G.vertices[u].data);

    for(w=FirstAdjVex(Rev_G,u);w>=0;w=NextAdjVex(Rev_G,u,w))
    {
        if(!visited[w])
        {
            DFS_transpose(Rev_G,w,visit);
        }
    }
}

void Reverse_graph(ALGraph G, ALGraph *Rev_G)
{
    int i;
    int v;
    int w;
    ArcNode *p;

    Rev_G->vexnum=G.vexnum;
    Rev_G->arcnum=G.arcnum;
    Rev_G->kind=G.kind;

    for(i=0;i<Rev_G->vexnum;i++)
    {
        Rev_G->vertices[i].data=G.vertices[i].data;
        Rev_G->vertices[i].firstarc=NULL;
    }

    for(v=0;v<G.vexnum;v++)
    {
        for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
        {
            p=(ArcNode *)malloc(sizeof(ArcNode));
            p->info = NULL;
            p->nextarc=NULL;
            p->adjvex=v;

            p->nextarc=Rev_G->vertices[w].firstarc;
            Rev_G->vertices[w].firstarc=p;
        }
    }
}