【数据结构】快速排序递归实现 _三种方法详解+优化

常见的排序算法有以上八种，所以预估会分成几期来讲，感兴趣的朋友们不妨点个收藏专栏。 ღ( ´･ᴗ･` )比心

OJ链接

---

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：

任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

将区间按照基准值划分为左右两半部分的常见方式: Hoare法、挖坑法、前后指针法。

快排又可以通过递归和非递归的方式进行实现。

Hoare法

核心思路

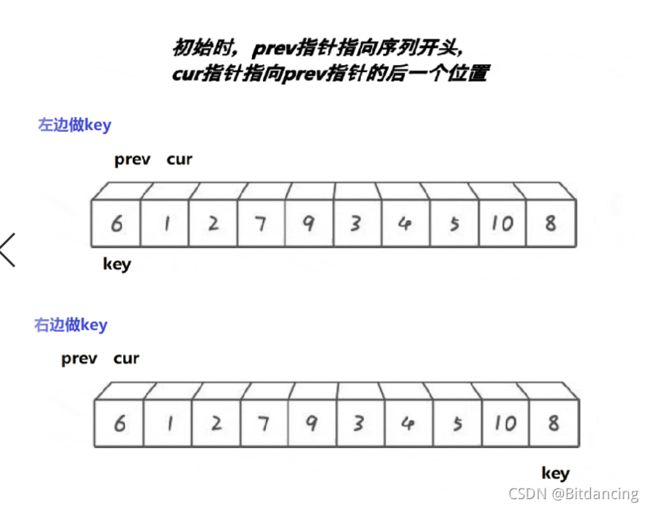
1. 当选择左边的值做key时，右边先走。
2. 当选择右边的值做key时，左边先走。

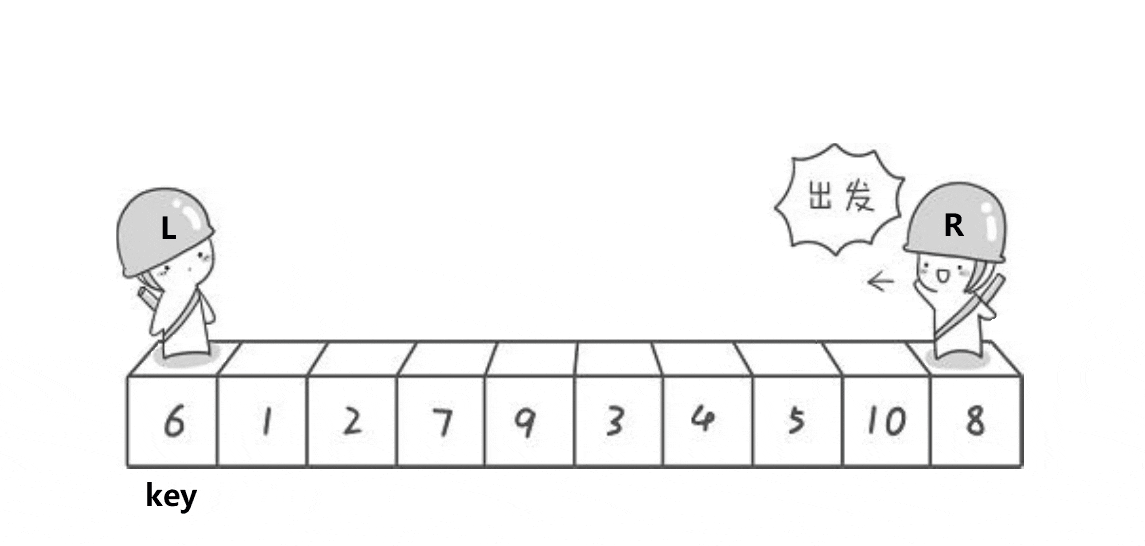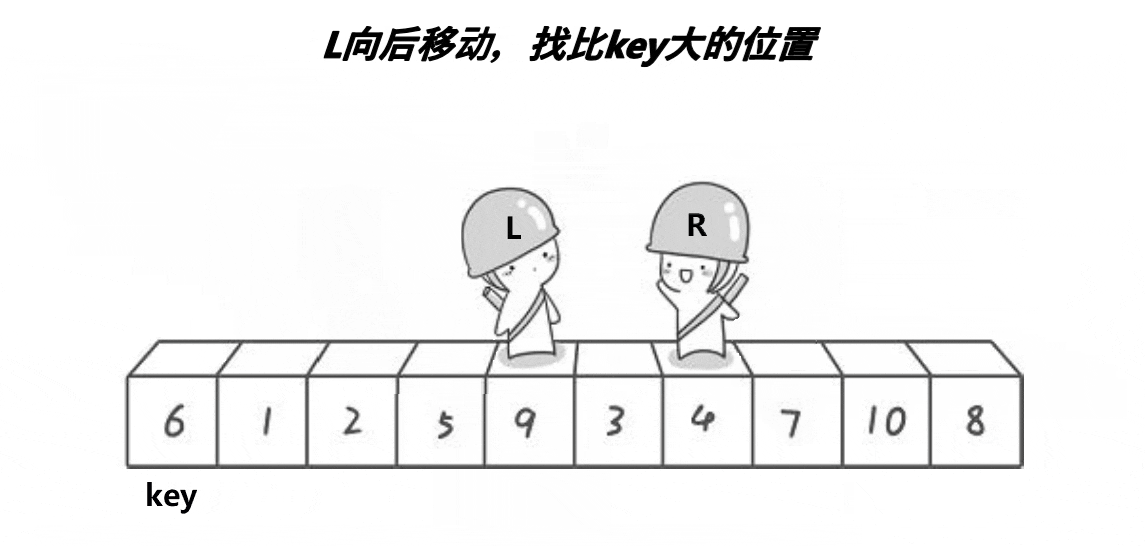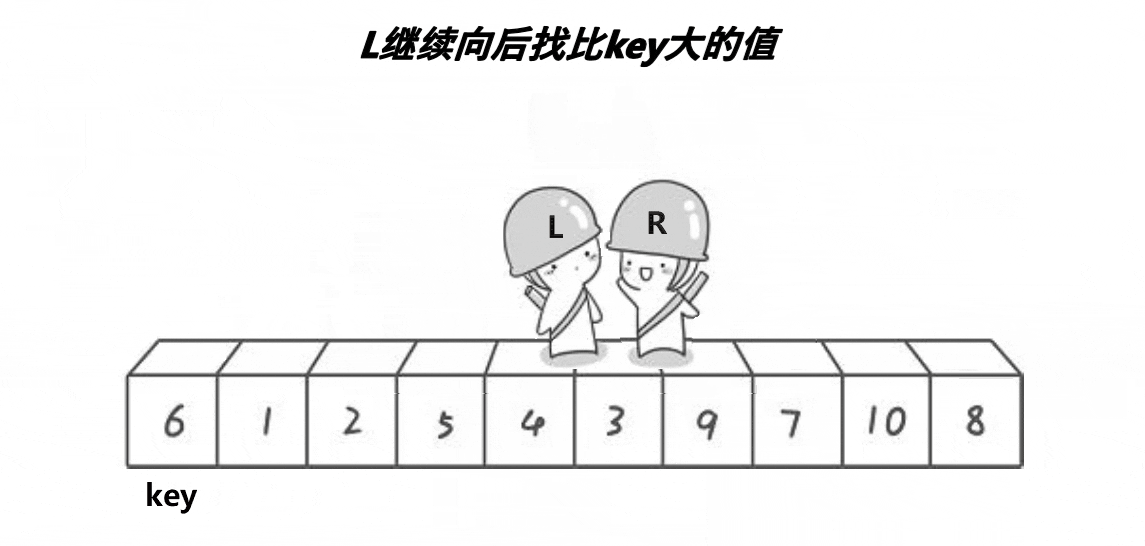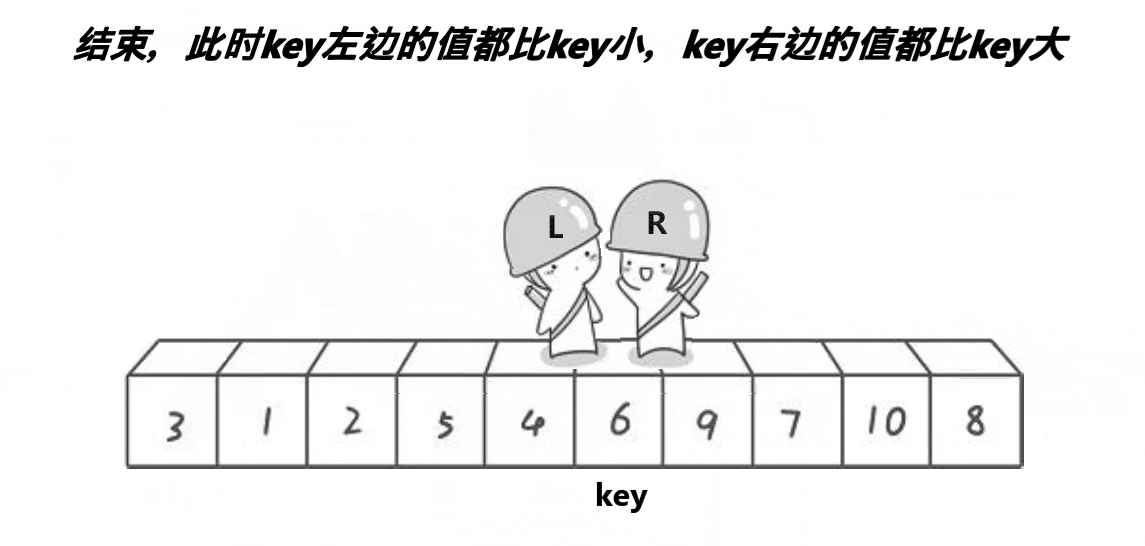
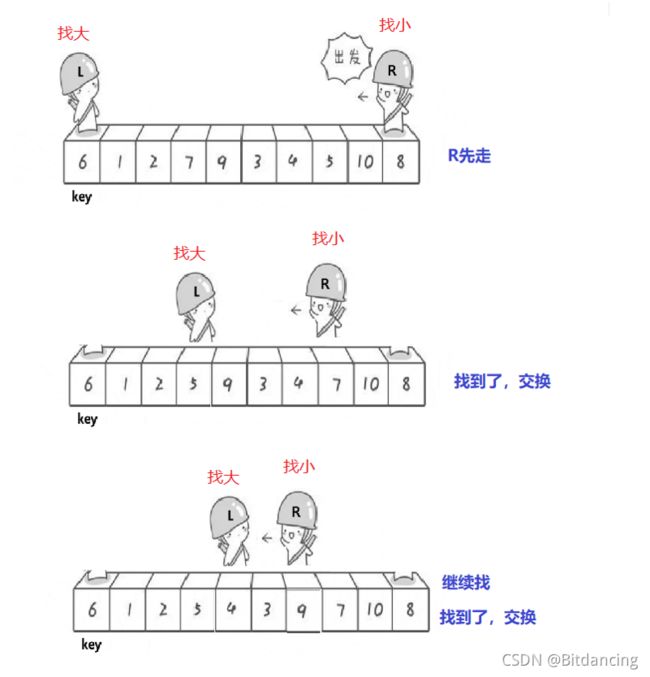
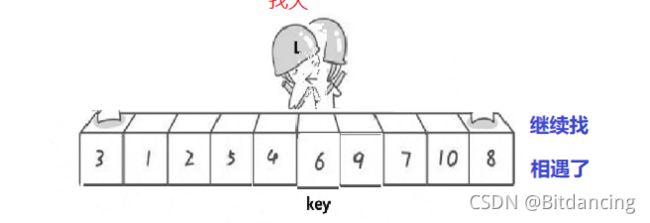
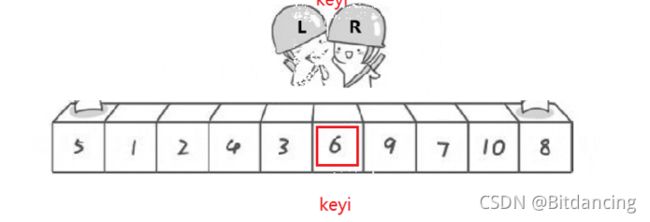
本文默认排升序，如图，选择左边值是key。右边先走，找比key小的值停下来，然后左边再走，找到比key大的停下来。交换左右两边的值，知道左右两者相遇。相遇点的值和key值交换。

图例分析

单趟程序

// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
	// 选择左边的值是key，右边开始走
	int keyi = left;
	while (left < right)
	{
		// left = right的时候，相遇break
		// 右边先走,找小
		while (left < right && a[right] >= a[keyi])
		{
			// 避免下标越界和死循环
			--right;
		}
		// 左边再走，找大
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}
		// 相遇的值和key交换
		Swap(&a[left], &a[keyi]);
	}
	return left;
}

挖坑法

Hoare版本变形。

核心思路

1、同样的，选择左边的值做key，右边先走；
2、选择右边的值做key，左边先走。

右边找小，把比key小的值放进坑里，右边形成新的坑；左边找大扔到坑里，左边形成新的坑。

挖坑法代码

// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
	// 选择左边的值做key，右边先走
	int key = a[left];
	int keyi = left;
	while (left < right)
	{
		// 右边先走，找小
		while (left < right && a[right] >= key)
		{
			--right;
		}
		// 找到了小，把小的放进坑里
		a[keyi] = a[right]; // a[right] < key
		keyi = right;

		// 左边再走，找大
		while (left < right && a[left] <= key)
		{
			++left;
		}
		// 找到了大，把大的放进坑里
		a[keyi] = a[left];
		keyi = left;
	}
	// left = right
	// 把keyi值放回坑里
	a[keyi] = key;
	return keyi;
}

前后指针法

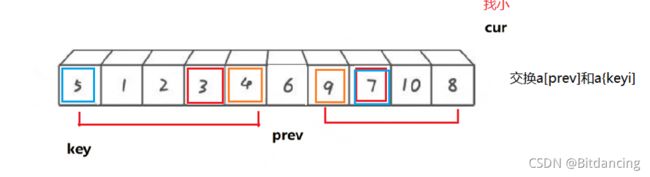
key选择不同，prev和cur的位置也不同。

当左边的值做key时，cur找比key小的值，找到比key小的值就停下来，++prev，交换prev和cur的值。

前后指针法程序

// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
	// key在left位置
	int keyi = left;
	int prev = left, cur = left + 1;
	while (cur <= right)
	{
		// cur向后找小，找到小的，++prev然后和cur交换
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[prev], &a[cur]);
		}
		++cur; //cur向后继续找
	}
	// 交换prev和key的值，prev此时是比key小的值
	Swap(&a[prev], &a[keyi]);
	return prev;
}

快排分析+优化

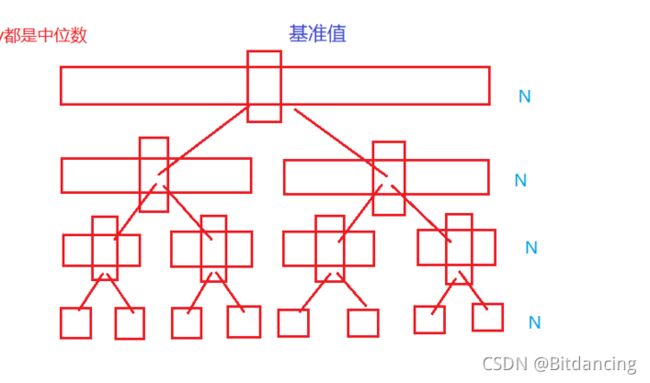
对于理想的快排，每次基准值如下：

时间复杂度是 O(N*logN)

但是当数组是有序时：

快排退化成冒泡排序。

解决方法：
1、随机取key值
2、三数取中。

但是三数取中 遇到数组元素相同的情况又会失效。

三数取中：

int GetMidValIndex(int* a, int left, int right)
{
	int mid = left + ((right - left) >> 1);
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

快排递归实现

快速排序的递归实现类似二叉树的前序遍历过程。

先使用Hoare、挖坑法或者前后指针法进行单趟排序，再通过递归分别处理左区间和右区间。

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	// 小区间优化
	if (right - left + 1 < 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{	
		int keyi = PartSort3(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}

空间复杂度： O(logN)