快速排序的递归实现和非递归实现

一、快速排序的递归实现

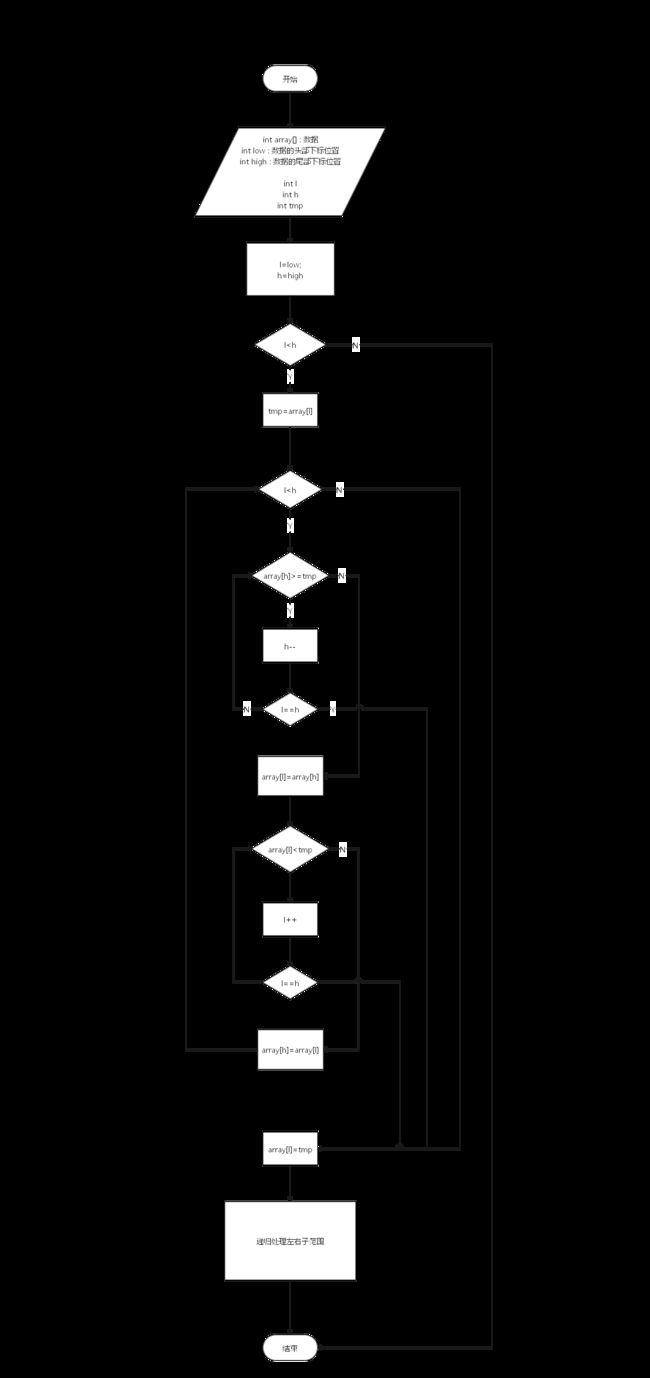
快速排序的思想是每次找到一个元素的位置，再在以这个元素分隔的两个子范围中分别再各自确定一个元素的位置，子子范围也是如此操作，当某个子范围只有一个元素或者没有元素时，便不再做任何操作。这是一个递归过程，递归退出的边界就是子范围中不存在元素或者只存在一个元素。

基于这个思想，很容易便得到递归处理的程序框图：

代码：

#include 

using namespace std;

static void quickSort(int array[],int low,int high){
    int l=low,h=high,tmp;
    if (l<h){
        tmp=array[l];
        while (l<h){
            while (array[h]>=tmp){
                h--;
                if(l == h){
                    goto complete;
                }
            }
            array[l]=array[h];

            while (array[l]<tmp){
                l++;
                if(l == h){
                    goto complete;
                }
            }
            array[h]=array[l];
        }

        complete:
        array[l]=tmp;
        //递归处理左右的序列
        quickSort(array,low,l-1);
        quickSort(array,h+1,high);
    }
}

int main() {
	//测试
    int a[8]={49,38,65,97,76,13,27,49};
    quickSort(a,0,7);
    for (int i = 0; i < 8; i++) {
        printf("%d ",a[i]);
    }
    return 0;
}

二、快速排序的非递归实现

上述递归实现的局限性可能在于：当数据量特别大时，可能会导致栈溢出(栈涨的速度为${\log }_{2}n$，也可能是我多虑了，涨地其实挺慢的)。

为了解决上面可能出现的问题，我们可以将递归实现转换为非递归实现，我们知道任何递归的过程都可以转化为一个迭代的过程，而转化的关键在于如何使用迭代来模拟整个递归的处理。

观察上面的递归处理过程，我们可以看到：每一次排序函数的调用都会再次重新调用两次新的排序函数，然后系统会按照调用顺序一步一步地进行处理和返回，而调用排序函数的关键在于必须将排序的范围告诉函数。

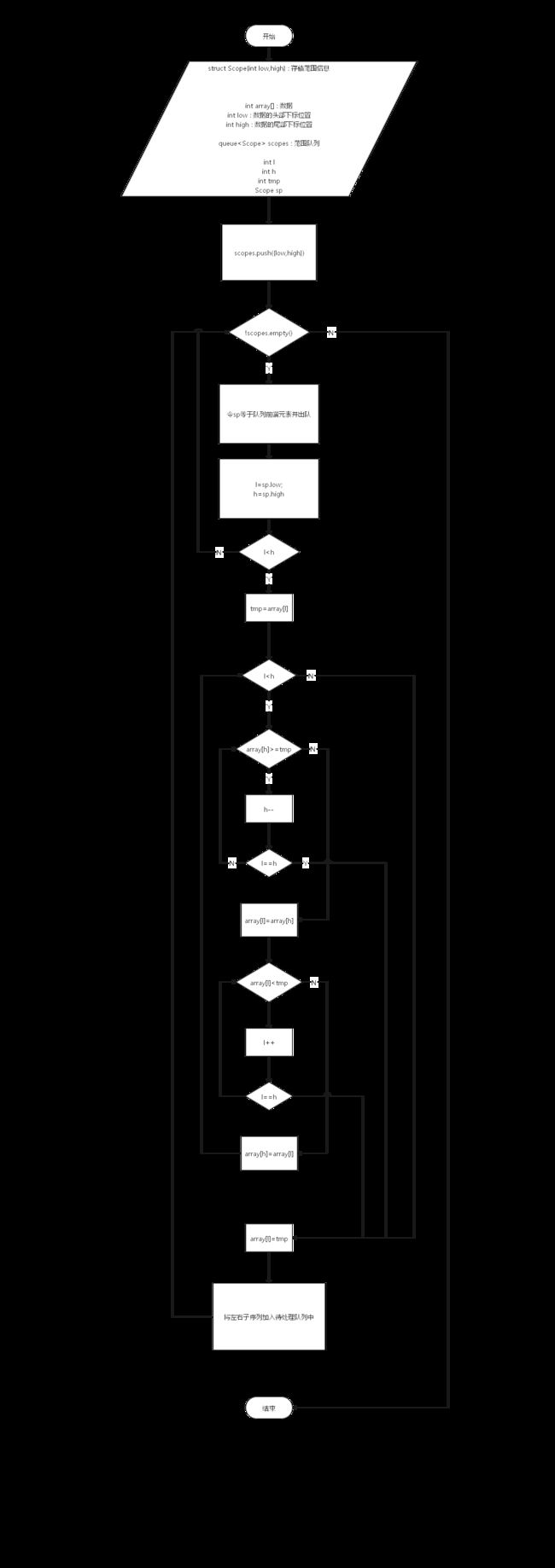
这个过程很像一个排队处理的过程，于是我们可以使用队列进行递归的模拟，而队列中的信息存储要处理的范围即可。当队列不为空时，表示还有范围未处理；队列为空时，表示所有的范围都已经处理完毕，也即确定了所有元素的位置，完成了排序工作。

于是我们可以得到下面非递归处理的程序框图：

代码：

#include 
#include 

using namespace std;

struct Scope{
    int low,high;
};

static void quickSort2(int array[],int low,int high){
    queue<Scope> scopes;
    scopes.push({low,high});
    Scope sp;
    while (!scopes.empty()){
        sp = scopes.front();
        scopes.pop();
        int l=sp.low,h=sp.high,tmp;
        if (l<h){
            tmp=array[l];
            while (l<h){
                while (array[h]>=tmp){
                    h--;
                    if(l == h){
                        goto complete;
                    }
                }
                array[l]=array[h];

                while (array[l]<tmp){
                    l++;
                    if(l == h){
                        goto complete;
                    }
                }
                array[h]=array[l];
            }

            complete:
            array[l]=tmp;
            //将左右子序列加入待处理队列中
            scopes.push({sp.low,l-1});
            scopes.push({h+1,sp.high});
        }
    }
}

int main() {
	//测试
    int a[8]={49,38,65,97,76,13,27,49};
    quickSort2(a,0,7);
    for (int i = 0; i < 8; i++) {
        printf("%d ",a[i]);
    }
    return 0;
}