自学算法
关于本课程
hi,少年。咱们来一起学习算法啦。这套课程特别适合自学算法的小白。每节课程最后还有一道练习题,边学边练,可以帮你及时巩固学习到的知识。
如果您在学习其他相关的算法课程,也可以学习该课程用来巩固知识点。
本教程中的练习题,请移步 1024乐学编程-算法基础 进行练习。
您也可以在该网站免费学习到更多课程
好,那我们正式开始!
算法,可以简单理解为,完成一个任务的方法。
你可以把它想象成食谱。要想做出一道菜肴,只需要按食谱的步骤一步步操作。
编程中的算法,就是用计算机解决一个问题的方法。
食谱和算法的最大区别,在于算法是严密的,只要遵循步骤就一定能解决特定的问题;而食谱经常会有模糊描述的部分,不同厨师按照一个食谱做出来的菜可能口味天差地别。
算法有优劣之分
算法也有优劣之分,如果让你在图书馆找到一本书
算法一:在图书馆乱逛,随便抓起一本书看是不是要找的,如果不是,就再逛到另一个地方,随便抓起一本书
算法二:从图书馆的第一排书架最顶层开始,从左到右,一本本地找。找完一层,再找下一层。如果整个书架找完了,就到下一个书架,再这样找。
算法三:根据图书的索引编号,到图书馆的特定区域(如文学区、科技区),找到编号对应的书架、在哪一层,然后从左到右一本本找到。
那肯定选择算法三! 效率最高。
时间复杂度
算法的优劣有很多体现,比如时间复杂度,空间复杂度,可读性和健壮性等等。
空间复杂度是指运行完一个程序所需内存的大小。一般来说,空间复杂度越小,算法越好。
时间复杂度用来衡量一个算法的运行时间和输入规模的关系,通常用 O表示。
简单计算复杂度的方法一般是统计“简单操作”的执行次数,有时候也可以直接数循环的层数来近似估计。
按增长量级递增排列,常见的时间复杂度有:
O(1)—常数阶
O(N)—线性阶
O(log2N)—对数阶
O(nlogn)—线性对数阶
O(n²)—平方阶
算这个时间复杂度实际上只需要遵循如下守则:
• 用常数1来取代运行时间中所有加法常数;
• 只要高阶项,不要低阶项;
• 不要高阶项系数;
O(1)的算法是一些运算次数为常数的算法。例如:
temp=a;
a=b;
b=temp;
根据守则:用常数1来取代运行时间中所有加法常数;
上面语句共三条操作,单条操作的频度为1,即使他有成千上万条操作,也只是个较大常数,这一类的时间复杂度为O(1);
O(n)的算法是一些线性算法。例如:
sum=0;
for(i=0;i上面代码中第一行频度1,第二行频度为n,第三行频度为n,所以f(n)=n+n+1=2n+1。
根据守则:只要高阶项,不要低阶项目,常数项置为1,去除高阶项的系数:
所以时间复杂度O(n)。这一类算法中操作次数和n正比线性增长。
之后我们会讲到二分查找的时间复杂度是O(Log2N);线性对数阶就是在LogN的基础上多了一个线性阶O(nlogn);
普通嵌套循环,它的时间复杂度为O(n²)。
for (int i = 0; i < n; i++) {//执行n次
for (int j = 0; j < n; j++) {//执行n次
}
}
插入排序
下面说们说一个简单的排序算法,在我们生活的这个世界中到处都是被排序过的东西。站队的时候会按照身高排序,考试的名次需要按照分数排序,网上购物的时候会按照价格排序,电子邮箱中的邮件按照时间排序……可以说排序是无处不在。
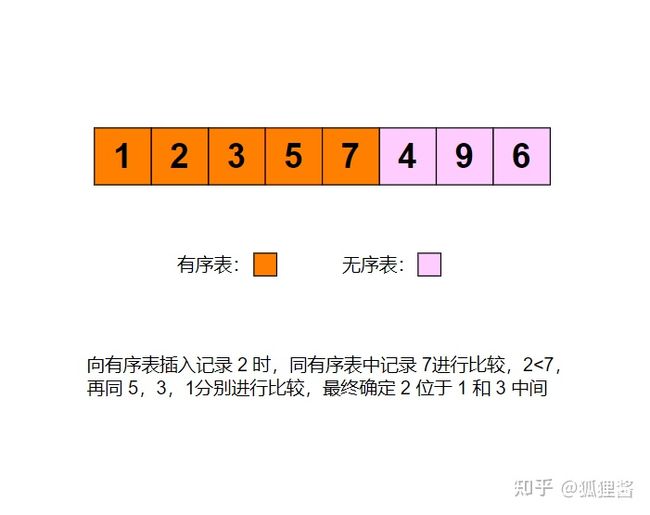
插入排序(英语:Insertion sort)是一种简单直观的排序算法。它的工作原理为将待排列元素划分为“已排序”和“未排序”两部分,每次从“未排序的”元素中选择一个插入到“已排序的”元素中的正确位置。
插入排序的最优时间复杂度为 ,在数列几乎有序时效率很高。
插入排序的最坏时间复杂度和平均时间复杂度都为 。
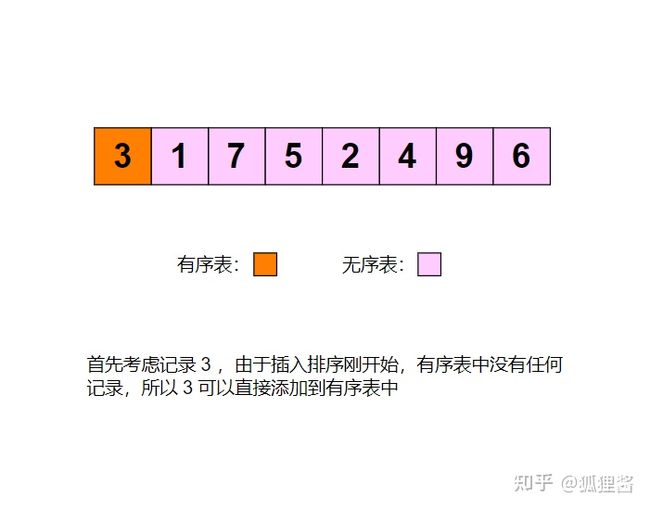
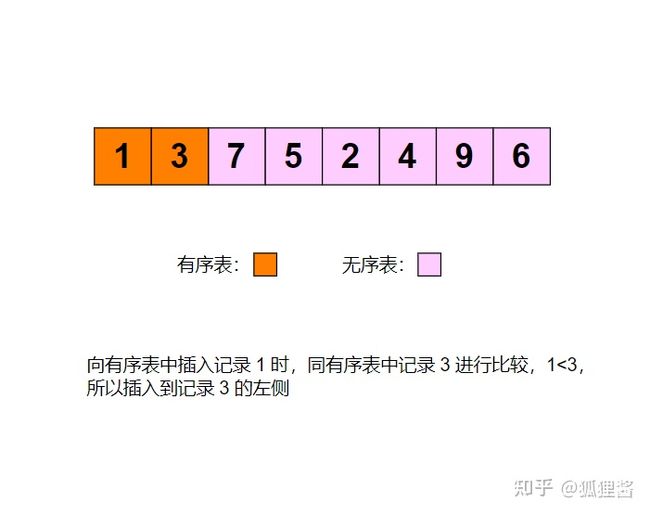
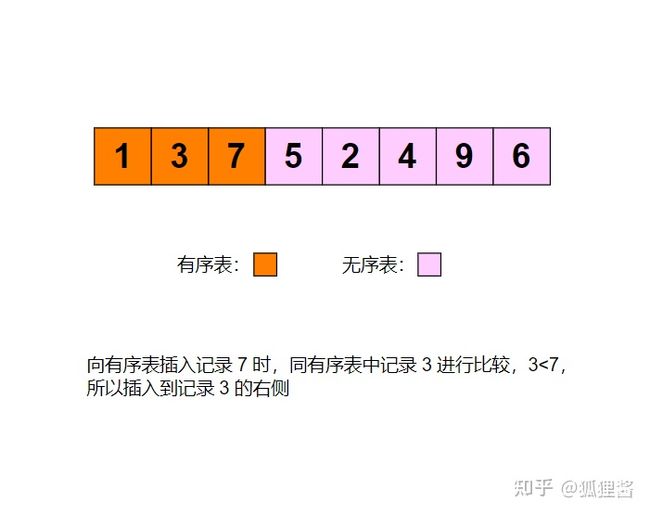
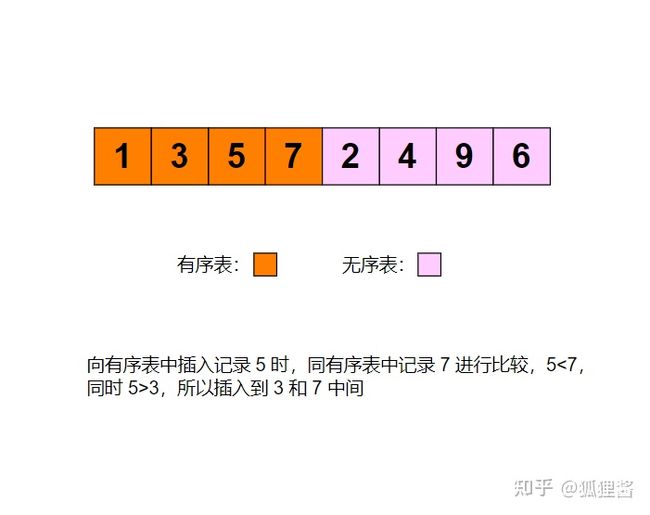
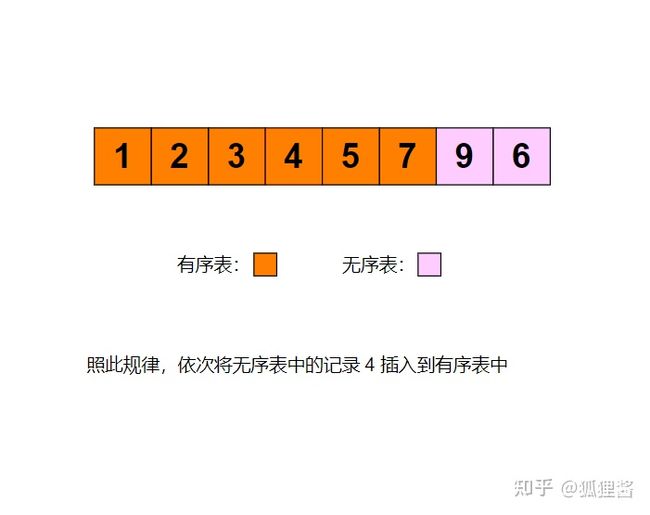
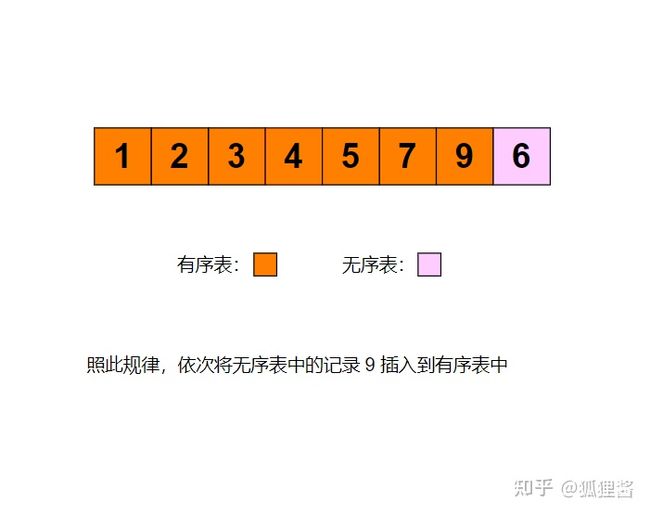
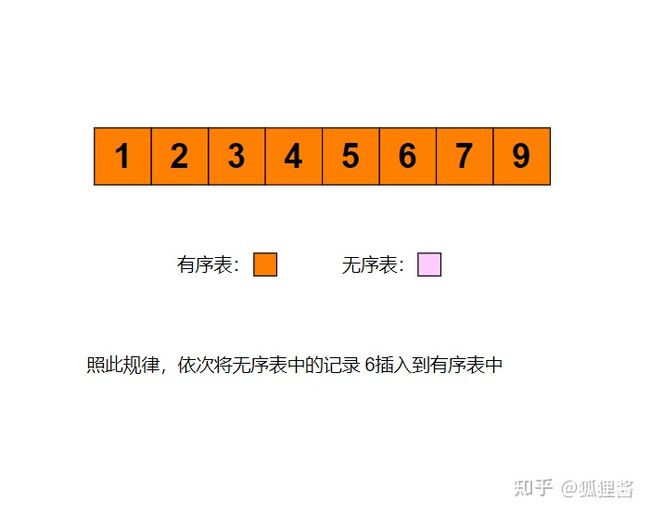
例如采用直接插入排序算法将无序表{3,1,7,5,2,4,9,6}进行升序排序的过程为:
代码实现
#include
using namespace std;
void InsertSort(int a[ ], int n)
{
for( int i = 1; i < n; i++ ){
if( a[ i ] < a[ i - 1 ]){ //若第 i 个元素大于 i-1 元素则直接插入;反之,需要找到适当的插入位置后在插入。
int j = i -1;
int x = a[ i ];
while( j > -1 && x < a[ j ]){ //采用顺序查找方式找到插入的位置,在查找的同时,将数组中的元素进行后移操作,给插入元素腾出空间
a[ j + 1 ] = a[ j ];
j--;
}
a[ j + 1 ] = x; //插入到正确位置
}
cout << i <<": ";
for (int k = 0; k < n; k++)
{
cout << a[ k ];
}
cout << endl;
}
}
int main()
{
int a[ 8 ] = {3, 1, 7, 5, 2, 4, 9, 6};
InsertSort(a, 8);
return 0;
}
直接插入排序的具体代码实现如上,运行结果为:
1: 13752496
2: 13752496
3: 13572496
4: 12357496
5: 12345796
6: 12345796
7: 12345679
接插入排序算法本身比较简洁,容易实现,该算法的时间复杂度为 O(n²)。
好,接下来我们做一道练习题,请移步到该网站的 《算法基础简介》课程中,习题在内容最后。
http://www.eluzhu.com:1818/my/course/65
冒泡排序
说说冒泡排序(英语:Bubble sort),它是一种简单的排序算法。由于在算法的执行过程中,较小的元素像是气泡般慢慢「浮」到数列的顶端,故叫做冒泡排序。
工作原理
它的工作原理是每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了。
冒泡排序是一种稳定的排序算法。
在序列完全有序时,冒泡排序只需遍历一遍数组,不用执行任何交换操作,时间复杂度为 。
在最坏情况下,冒泡排序要执行 次交换操作,时间复杂度为 。
冒泡排序的平均时间复杂度为 。
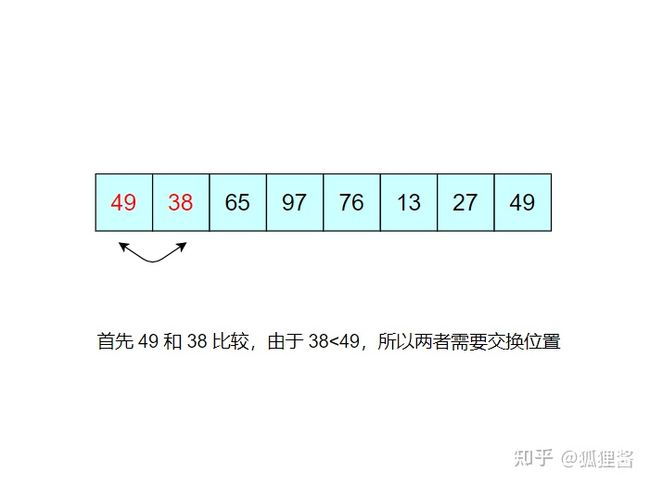
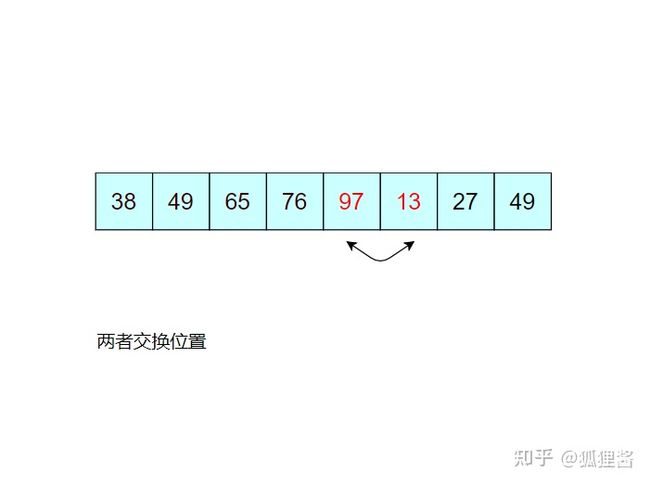
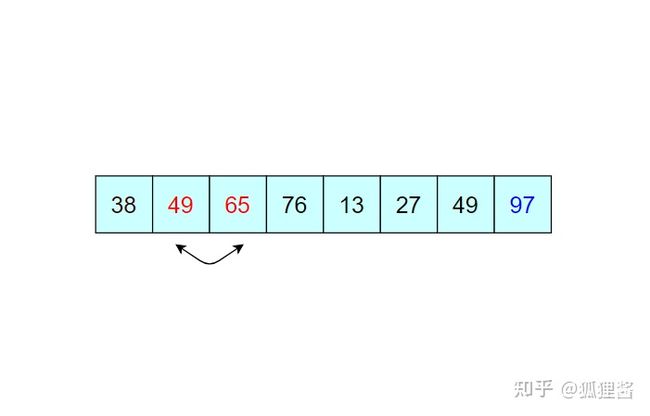
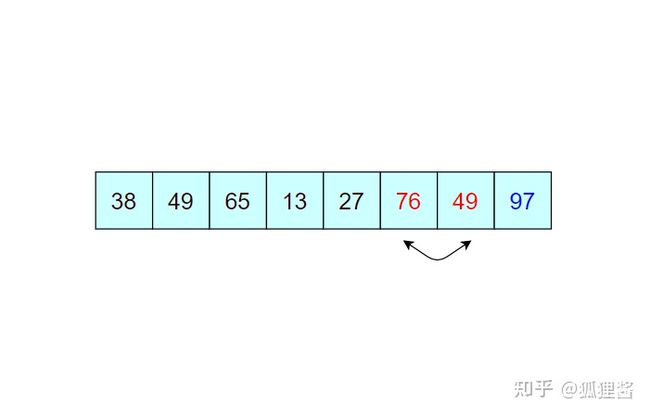
例如,对无序表{49,38,65,97,76,13,27,49}进行升序排序的具体实现过程如下所示
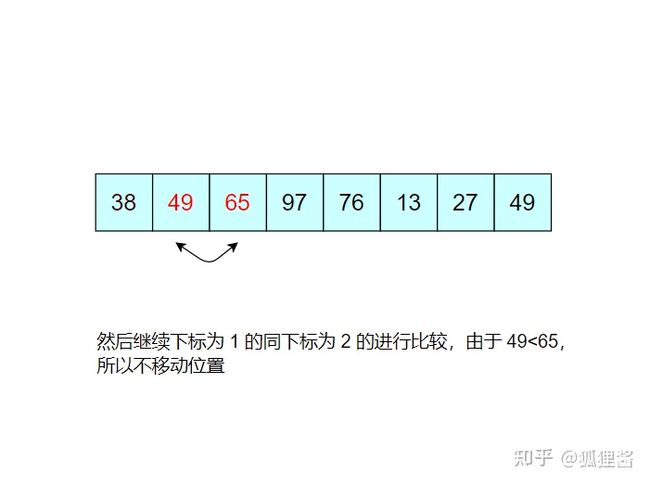
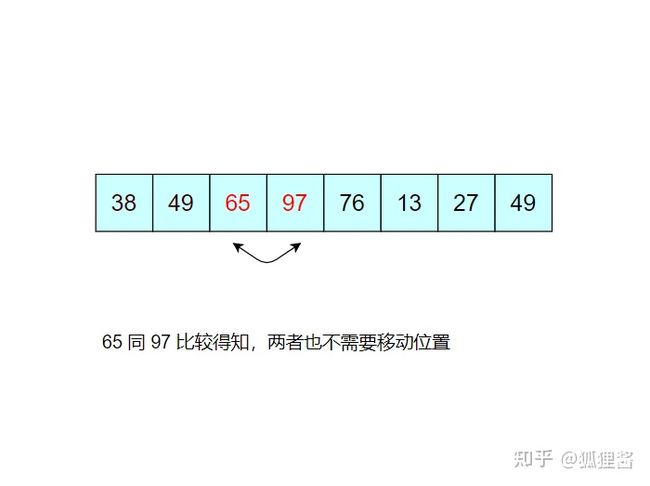
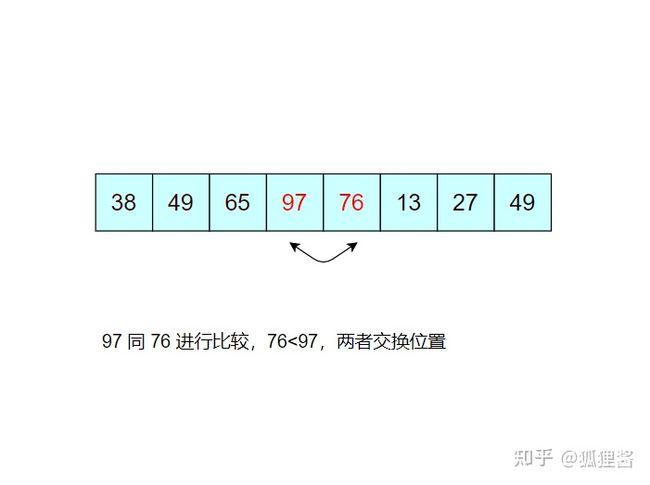
如图所示是对无序表的第一次冒泡排序,最终将无序表中的最大值 97 找到并存储在表的最后一个位置,第一次冒泡结束;
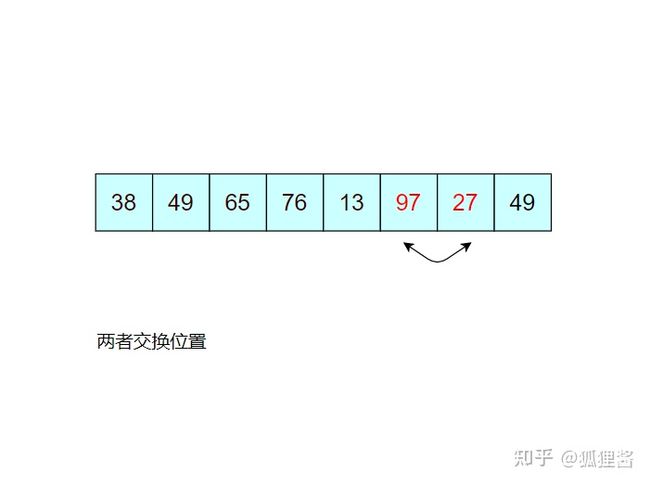
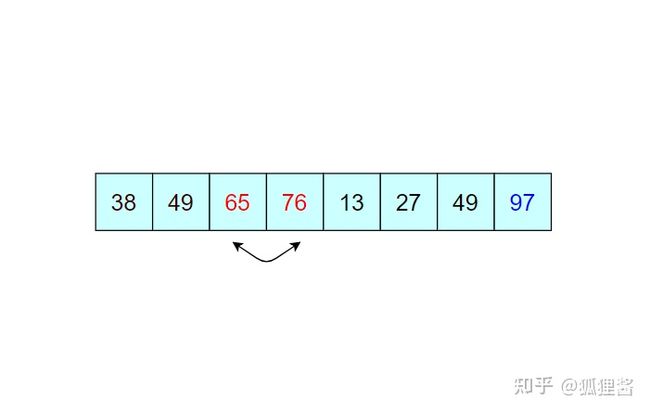
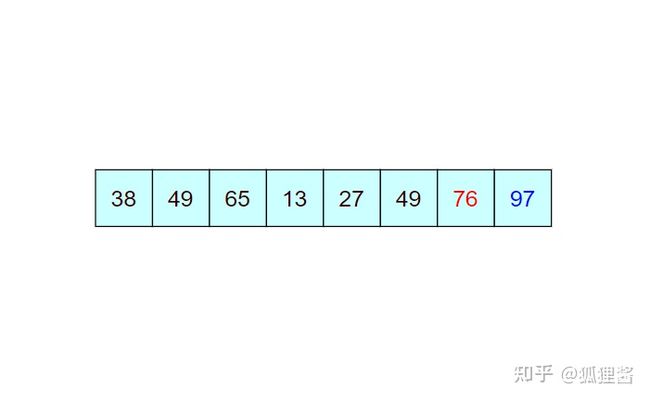
由于 97 已经判断为最大值,所以第二次冒泡排序时就需要找出除 97 之外的无序表中的最大值,比较过程和第一次完全相同。
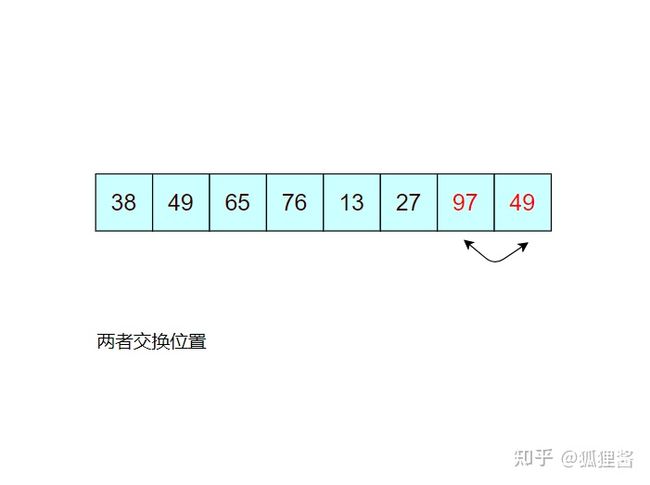
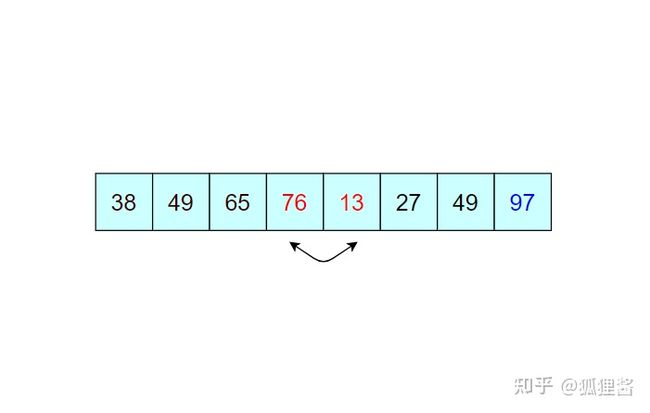
经过第二次冒泡,最终找到了除 97 之外的又一个最大值 76,比较过程完全一样,这里不再描述。
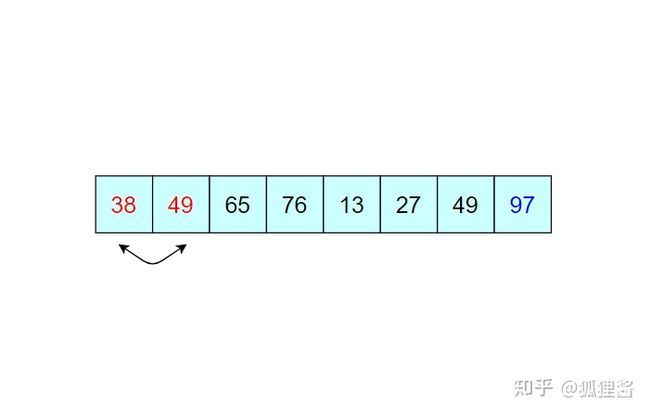
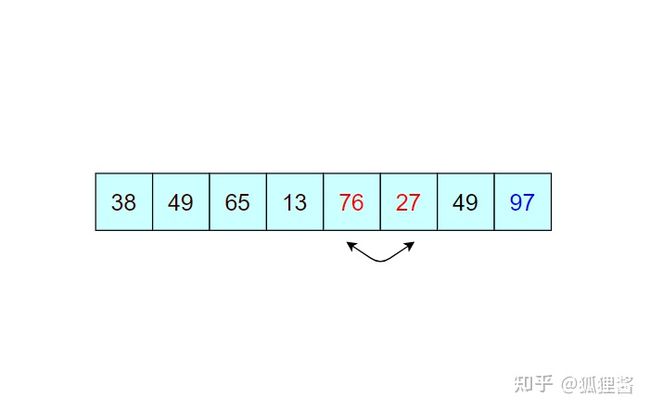
通过一趟趟的比较,一个个的“最大值”被找到并移动到相应位置,直到检测到表中数据已经有序,或者比较次数等同于表中含有记录的个数,排序结束,这就是冒泡排序。
具体实现代码为:
#include
using namespace std;
int main()
{
int array[ 8 ] = {49,38,65,97,76,13,27,49};
int i, j;
int key;
//有多少记录,就需要多少次冒泡,当比较过程,所有记录都按照升序排列时,排序结束
for (i = 0; i < 8; i++){
key = 0;//每次开始冒泡前,初始化 key 值为 0
//每次起泡从下标为 0 开始,到 8-i 结束
for (j = 0; j+1 < 8-i; j++){
if (array[ j ] > array[ j+1 ]){
key = 1;
int temp;
temp = array[ j ];
array[ j ] = array[ j+1 ];
array[ j+1 ] = temp;
}
}
if (key==0) {//如果 key 值为 0,表明表中记录排序完成
break;
}
}
for (i = 0; i < 8; i++){
cout<< array[ i ]<<" ";
}
return 0;
}
运行结果为:
13 27 38 49 49 65 76 97
冒泡排序的核心部分是双重嵌套循环。不难看出冒泡排序的时间复杂度是O(N²)。这是一个非常高的时间复杂度。冒泡排序早在1956年就有人开始研究,之后有很多人都尝试过对冒泡排序进行改进, 但结果却令人失望。如Donald E.Knuth(中文名为高德纳, 1974年图灵奖获得者)所说:“冒泡排序除了它迷人的名字和导致了某些有趣的理论问题这一事实之外,似乎没有什么值得推荐的。
快速排序
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这10个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,这就是一个用来参照的数,待会儿你就知道它用来做啥了)。为了方便,就让第一个数6作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在6的右边,比基准数小的数放在6的左边,类似下面这种排列:
3 1 2 5 4 6 9 7 10 8
在初始状态下,数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置,假设这个位置是k。现在就需要寻找这个k,并且以第k位为分界点,左边的数都小干等于右边的数都大于等于6。
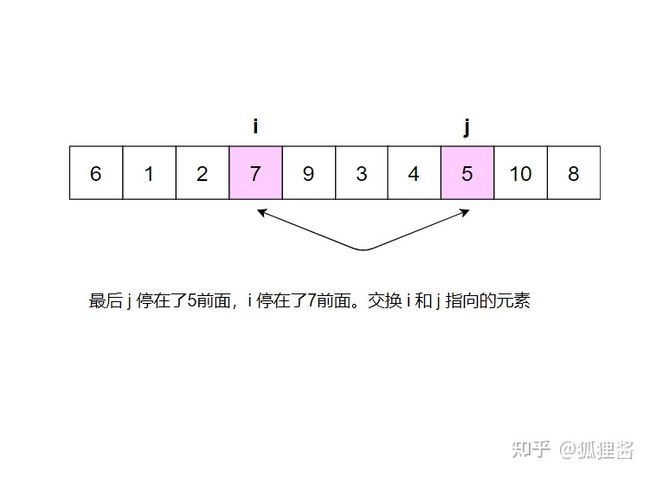
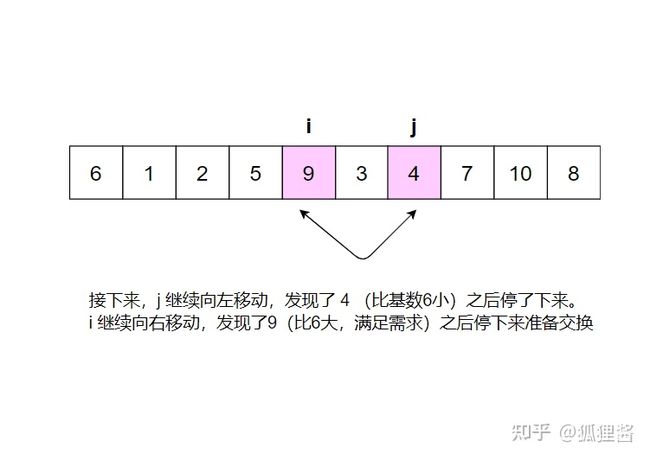
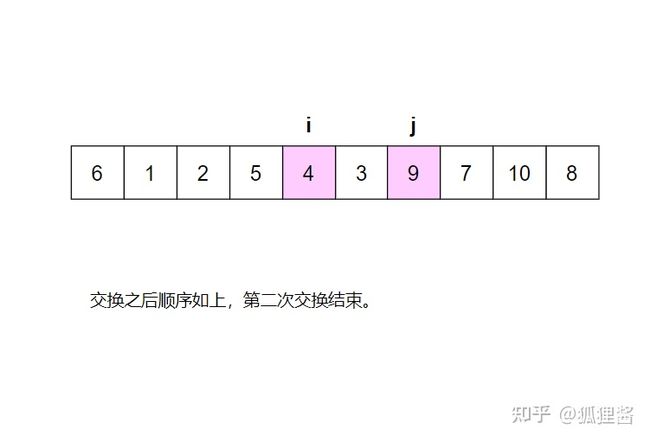
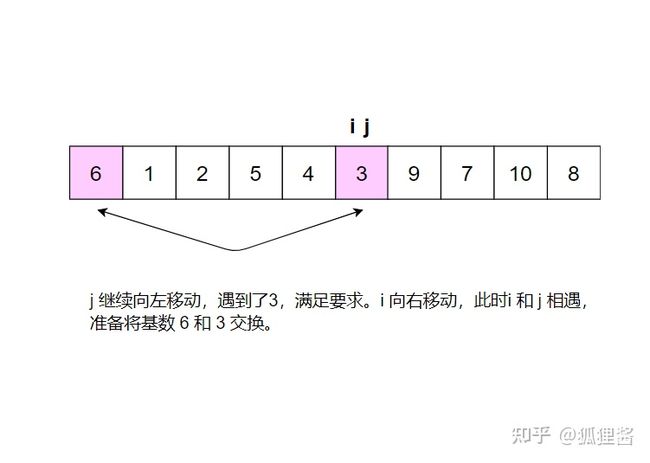
分别从初始序列“6 1 2 7 9 3 4 5 10 8"两端开始“探测"、先从右往左我一个小于6的数,再从左往右找一个大干6的教,然后交换它们。这里可以用两个变量 i 和 j ,分别指向最左和最右边。具体的流程请参考:
现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”,接下来还需要分别处理这两个序列,因为6左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列吧。
左边的序列是“3 1 2 5 4”。请将这个序列以3为基准数进行调整,使得3左边的数都小于等于3,右边的数都大于等于3。
快速排序之所以比较快,是因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样只能在相邻的数之间进行交换,交换的距离就大得多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的, 都是O(N) , 它的平均时间复杂度为O(N logN) 。我们先看看代码,如下。
#include
using namespace std;
//快速排序算法(从小到大)
//arr:需要排序的数组,begin:需要排序的区间左边界,end:需要排序的区间的右边界
void quickSort(int *arr, int begin, int end){
//如果区间不只一个数
if (begin < end){
int temp = arr[ begin ]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”,指示当前左位置
int j = end; //从右到左进行查找时的“指针”,指示当前右位置
//不重复遍历
while ( i < j ){
//当右边的数大于基准数时,略过,继续向左查找
//不满足条件时跳出循环,此时的j对应的元素是小于基准元素的
while (i < j && arr[ j ] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[ i ] = arr[ j ];
//当左边的数小于等于基准数时,略过,继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环,此时的i对应的元素是大于等于基准元素的
while (i < j && arr[ i ] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[ j ] = arr[ i ];
}
//将基准元素填入相应位置
arr[ i ] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr, begin, i - 1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr, i + 1, end);
}
//如果区间只有一个数,则返回
else
return;
}
int main(){
int num[10] = {6,1,2,7,9,3,4,5,10,8};
int n = 10;
quickSort(num, 0, n - 1);
cout << "排序后的数组为:" << endl;
for (int i = 0; i < n; i++)
cout << num[ i ] << ' ';
cout << endl;
return 0;
}
运行结果是:
1 2 3 4 5 6 7 8 9 10
选择排序
选择排序(英语:Selection sort)是排序算法的一种,它的工作原理是:对于具有 n 个记录的无序表遍历 n-1 次,第 i 次从无序表中第 i 个记录开始,找出后序关键字中最小的记录,然后放置在第 i 的位置上。
由于 swap(交换两个元素)操作的存在,选择排序是一种不稳定的排序算法。
选择排序的最优时间复杂度、平均时间复杂度和最坏时间复杂度均为 。
例如对无序表{56,12,80,91,20}采用简单选择排序算法进行排序,具体过程为如下幻灯片。
最后你来将选择排序的关键代码补全,请移步到该网站的 《排序算法》课程中,习题在内容最后。
1024乐学编程-算法基础
好,我们这次先讲到这里,请进入作者主页继续学习后续的算法课程。或进入上面的地址免费学习完整的算法课程。