2022 CCPC补题(更新中...)
2022 CCPC补题(更新中…)
看着学校的佬参加了CCPC和ICPC,自己作为一名准ACMer,就来把一些签到题做一下。
ps:恭喜我校的梭哈队获得银牌。
第一场 链接: 2022 CCPC桂林
A.Lily 签到
思路:比较简单的签到 ,直接循环遍历一遍遇到L我们就给它及其左右标记一下,最后没有标记到的点都是C,输出即可。
代码:
#include
#include M.Youth Finale 逆序对+维护
题意:给我们一个序列,给定两种操作,R表示将序列翻转(reverse),S表示将序列的首项移到尾项。
给你一个序列和一个操作字符串,求出将每次操作后得到的序列排序所需要使用swap函数次数(结果mod10)。
思路:求解冒泡函数中调用swap函数数量实际上等价于求解序列中逆序对的数量,所谓逆序对就是满足i
一开始我采用模拟的思路,每次操作模拟序列变化,很不幸,TLE了。我开始想方法优化,经过模拟,我用一个数组来存每个数当前的逆序对数量,我发现当对序列采用S操作时,首项会被放置到末项,那么首项的逆序对会变成0,并且所有大于首项的数的逆序对数量都会+1。所以我们维护好这个数组即可。对于R操作,我发现ans会变成n*(n+1)/2-ans。除了我们需要维护ans和数组的值,我们还需要维护序列的顺序。但是直接操作还是会超时,最后我想到了使用指针去指向数组的首项,这样我们只需要通过维护指针的位置,就可以维护序列的顺序。上代码(头文件和上面一样就不重复发了):
代码写的比较丑:(主要是优化到没心思去写好看了)
LL q[N],n,m,tmp[N],a[N];
LL merge_sort(int l,int r){
if(l>=r) return 0;
int mid=l+r>>1;
LL res=merge_sort(l,mid)+merge_sort(mid+1,r);
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r){
if(q[i]<=q[j]){
tmp[k++]=q[i++];
}
else{
tmp[k++]=q[j++];
res+=mid-i+1;
}
}
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++){
q[i]=tmp[j];
}
return res;
}
int main() {
io;
cin>>n>>m;
for(int i=0;i<n;i++) {cin>>q[i];a[i]=q[i];}
string ch;
cin>>ch;
LL ans=merge_sort(0,n-1);
cout<<ans<<endl;
int flg=0;//是否进行了翻转
int head=0;
for(int i=0;i<m;i++){
if(ch[i]=='S'){
//更新答案
ans-=a[head]-1;
ans+=n-a[head];
cout<<ans%10;
//优化后的更新状态
if(flg&1){
head--;
if(head<0) head=n-1;
}
else{
head++;
if(head>=n) head=0;
}
}
else{
//更新答案
LL tt=(n-1)*n/2;
ans=tt-ans;
cout<<ans%10;
//更新状态
flg++;
if(flg&1){
head--;
if(head<0) head=n-1;
}
else{
head++;
if(head>=n) head=0;
}
}
}
return 0;
}
C.Array Concatenation 数学规律+思维
题意:
给你一个序列b,你有两种操作第一种是复制一个b放在原序列后面,第二种操作时翻转b序列放在原序列前面,让你求这个式子的最大值。

思路:观察这个式子字其实就是把前缀和的数组再求一个和。这个我是先模拟,寻求一个规律,总结出每种操作对结果的贡献,然后经过模拟,发现其实进行了一次翻转操作后,后续的两种操作都是等价的,所以我们直接对序列b进行n次第一种操作,得出ans1,在对b序列进行n次第二种操作,得到ans2,最后取最大值即可,这里题目要求取模,公式一定写对。具体实现看代码吧。有点久远了,我有点忘记。
代码:
LL a[N],s[N];
LL n,m;
LL ans;
//快速幂板子
LL qmi(LL a, LL b, LL p)
{
LL res = 1 % p;
while (b)
{
if (b & 1) res = res * a % p;
a = a * (LL)a % p;
b >>= 1;
}
return res;
}
int main() {
io;
cin>>n>>m;
LL sum=0,sum1=0,res=0;
for(int i=1;i<=n;i++) {
cin>>a[i];
s[i]=((s[i-1]%mod)+(a[i]%mod))%mod;
res=((res%mod)+(s[i]%mod))%mod;
}
sum=s[n]%mod;
sum1=sum;
LL nn=n;
for(int i=0;i<m;i++){
LL s1=((n%mod)*(sum%mod))%mod;
LL s2=(2*(res%mod))%mod;
res=((s2%mod)+(s1%mod))%mod;
n=(2*(n%mod))%mod;
sum=(2*(sum%mod))%mod;
}
LL ss1=((qmi(2,m,mod)*nn)%mod+1)%mod;
LL ss2=(qmi(2,m-1,mod)*(sum1%mod))%mod;
LL res2=((ss1%mod)*(ss2%mod))%mod;
cout<<max(res,res2)<<endl;
return 0;
}
其余题目待补…
第二场 链接: 2022CCPC威海
前两天的比赛,最近抽空写了三题,后续题目待补。
签到题的两题还是非常顺利的。
E.Python Will be Faster than C++ 签到+思维
思路:我们要找第一个满足a[i]
LL a[N];
int main() {
io;
LL n,k;
cin>>n>>k;
LL ans;
bool f=0;
for(int i=1;i<=n;i++){
cin>>a[i];
if(a[i]<k){ans=i;f=1;}
}
if(f) {cout<<"Python 3."<<ans<<" will be faster than C++"<<endl;return 0;}
LL a1=a[n],d=a[n]-a[n-1];
if(d>=0) {cout<<"Python will never be faster than C++"<<endl;return 0;}
int i=0;
while(a1>=k){
i++;
a1+=d;
}
ans=n+i;
cout<<"Python 3."<<ans<<" will be faster than C++"<<endl;
return 0;
}
A.Dunai 贪心
题意:先给你所有得过冠军的选手名字,然后再给你一些选手和他们的位置,让你求出能够组成的战队数量的最大值。战队要求:每个选手只能去一个战队,每个战队必须要有一名冠军选手,每个战队必须五个位置的选手都有。
思路:很显然,战队的最大人数是由冠军选手数量和最少位置选手数量决定的。为了使战队人数最大,那么每个战队我们就安排一名冠军选手,并且由于位置不能冲突,所以统计冠军数量时,我们需要和最小位置人数进行取最小值。
最后就是存储的问题。这里我采用了两个map,一个来存每个选手的位置,一个来存每个选手是否得过冠军。
用两个数组,一个来存每个位置的选手人数,一个来存每个位置冠军人数。
最后直接操作即可。
代码:
unordered_map<string,int> player;
unordered_map<string,int> ischam;
int chamcnt[10],playcnt[10];
int main() {
io;
int n,m;
cin>>n;
for(int i=0;i<5*n;i++){
string s;
cin>>s;
ischam[s]=1;
}
cin>>m;
for(int i=0;i<m;i++){
string s;
int x;
cin>>s>>x;
playcnt[x]++;
player[s]=x;
if(ischam[s])
chamcnt[x]++;
}
int posmin=*min_element(playcnt+1,playcnt+6);
int sum=0;
for(int i=1;i<6;i++){
sum+=min(chamcnt[i],posmin);
}
int ans=min(sum,posmin);
cout<<ans<<endl;
return 0;
}
G. Grade 2 思维
题意:题目很直接,给你一个x,并且给n个询问,每次给你l,r。让你求这个值。
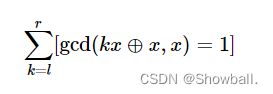
也就是从l到r满足中间的式子为1的个数。
思路:这个题的数据给的很大,很明显不能暴力,看到询问的数据给到了1012次方那么只可以O(1)来解决。类比前缀和,我们采用O(n)复杂度求出a[n],那么l,r之间直接用a[r]-a[l-1]求解即可。先写个暴力打一下表很明显就发现了gcd的结果具有周期性,并且发现偶数的倍数也是偶数,那么二进制下的最后一位都是0,异或后还是0,所以gcd之后的结果不可能为1,那么直接输出0即可,开始打表研究奇数情况下的周期,发现1的周期是1,3的周期是4,5的周期是8,7的周期是8,9的周期是16,以此类推。所以我们发现每个奇数的周期就是第一个大于它的2的n次方数。那么写个循环即可算出来,剩下的就是常规操作了,整除+取模即可。看代码:
注意数组要多开大10000,因为当x为999999时它的周期是要超过1000000的。
const int N=1100000;
LL a[N];
LL T(LL x){
int ans=1;
while(ans<x){
ans<<=1;
}
return ans;
}
int main() {
io;
LL n,x;
cin>>x>>n;
bool flg=0;
LL t;
if(x&1){
t=T(x);
for(LL i=1;i<=t;i++){
if(gcd((i*x)^x,x)==1) {a[i]=a[i-1]+1;}
else
a[i]=a[i-1];
}
}
else flg=1;
while(n--){
LL l,r;
cin>>l>>r;
if(flg) {cout<<0<<endl;continue;}
LL ans=(r/(t))*a[t]+a[r%(t)]-(((l-1)/t)*a[t]+a[(l-1)%t]);
cout<<ans<<endl;
}
return 0;
}
其余题目待补…
恰饭去了,继续加油!