数据包络分析DEA(数学建模)
一、模型背景
数据包络分析是线性规划模型的应用之一,常被用来衡量拥有相同目标的运营单位的相对效率。
数据包络分析是一种基于线性规划的用于评价同类型组织(或项目)工作绩效相对有效性的特殊工具手段。这类组织例如学校、医院、银行的分支机构、超市的各个营业部等,各自具有相同(或相近)的投入和相同的产出。衡量这类组织之间的绩效高低,通常采用投入产出比这个指标,当各自的投入产出均可折算成同一单位计量时,容易计算出各自的投入产出比并按其大小进行绩效排序。
但当被衡量的同类型组织有多项投入和多项产出,且不能折算成统一单位时,就无法算出投入产出比的数值。例如,大部分机构的运营单位有多种投入要素,如员工规模、工资数目、运作时间和广告投入,同时也有多种产出要素,如利润、市场份额和成长率。在这些情况下,很难让经理或董事会知道,当输入量转换为输出量时,哪个运营单位效率高,哪个单位效率低。
因而,需采用一种全新的方法进行绩效比较。这种方法就是二十世纪七十年代末产生的数据包络分析((DEA )。DEA方法处理多输入,特别是多输出的问题的能力是具有绝对优势的。
DEA模型是直接使用输入、输出数据建立非参数的经济数学模型。
DEA特别适用于具有多输入多输出的复杂系统,这主要体现在以下几点:
DEA以决策单位各输入/输出的权重为变量,从最有利于决策单元的角度进行评价,从而避免了确定各指标在优先意义下的权重;
假定每个输入都关联到一个或者多个输出,而且输入/输出之间确实存在某种关系,使用DEA方法则不必确定这种关系的显示表达式。
二、模型介绍
1、评价思想
核心是通过对每个DMU的输入和输出数据进行综合分析,得出每个DMU效率的相对指标,然后将所有DMU效率指标排序,确定相对有效的DMU即有效的决策单元,为管理人员提供管理决策信息
举个例子,每个公司的各个部门可以看成是每个DMU,因为每个部门有输入成本和产出效益
2、DEA基本概念
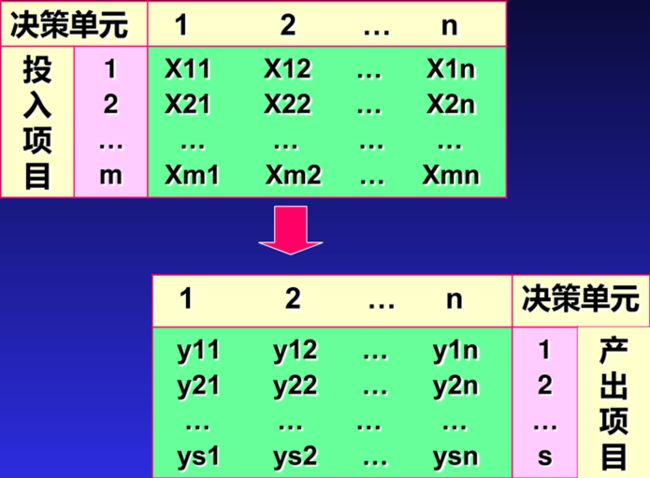
在DEA中一般称被衡量绩效的组织为决策单元( decision makingunit—DMU )。
设:n个决策单元( j=1,2 ,...,n )
每个决策单元有相同的m项投入(输入)(i =1 ,2 ,...,m )
每个决策单元有相同的s项产出(输出)(r=1,2 ,...,s )
Xij——第j决策单元的第i项投入
yrj——第j决策单元的第r项产出衡量第j0决策单元是否DEA有效
3、结果
①θ=1,DEA有效,表示投入与产出比达到最优
②θ<1,非DEA有效,表示投入与产出比没有达到最优,一般来说,θ越大说明效果越好。
数据包络分析是通过对投入的指标和产出的指标做了一个线性规划,并且进行变换后,然后根据其线性规划的对偶问题(线性规划对偶问题具有经济学意义),求解这个对偶问题的最值就是θ。
三、实例分析
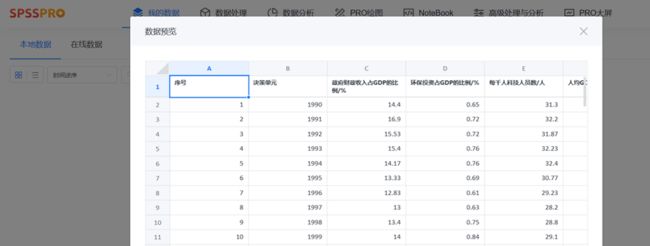
1、spsspro上传数据
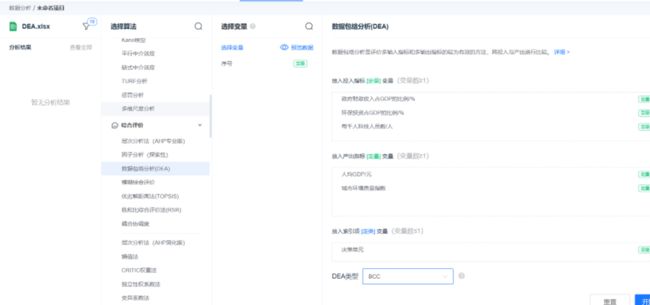
输入变量:政府财政收入占GDP的比例、环保投资占GDP的比例、每千人科技人员数。
输出变量:经济发展(用人均GDP表示)、环境发展(用城市环境质量指数表示;计算过程中,城市环境指数的数值作了 归一化处理)。
2、选择输入输出变量
3、效益分析表
决策单元 |
技术效益 |
规模效益 |
综合效益 |
松弛变量S- |
松弛变量S+ |
有效性 |
1990 |
0.938 |
0.309 |
0.290 |
0.926 |
0.132 |
非DEA有效 |
1991 |
0.876 |
0.326 |
0.285 |
0.586 |
0.054 |
非DEA有效 |
1992 |
0.885 |
0.335 |
0.297 |
0.241 |
0.084 |
非DEA有效 |
1993 |
0.875 |
0.391 |
0.343 |
0.144 |
0.082 |
非DEA有效 |
1994 |
0.905 |
0.507 |
0.459 |
2.172 |
0.000 |
非DEA有效 |
1995 |
0.977 |
0.735 |
0.718 |
6.246 |
582.860 |
非DEA有效 |
1996 |
1.000 |
0.907 |
0.907 |
5.505 |
0.000 |
非DEA有效 |
1997 |
1.000 |
1.000 |
1.000 |
0.000 |
0.000 |
DEA强有效 |
1998 |
1.000 |
1.000 |
1.000 |
0.000 |
0.000 |
DEA强有效 |
1999 |
1.000 |
1.000 |
1.000 |
0.000 |
0.000 |
DEA强有效 |
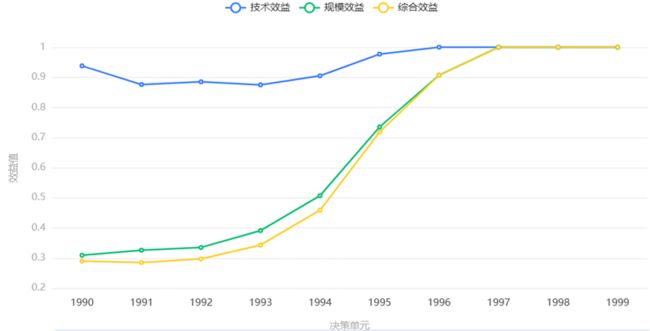
BCC模型(VRS)把综合效益分解为技术效益和规模效益。
● 综合技术效益(overall efficiency, OE)反映的是决策单元在一定(最优规模时)投入要素的生产效率,是对决策单元的资源配置能力、资源使用效率等多方面能力的综合衡量与评价,值等于1时,代表该决策单元的投入与产出结构合理,相对效益最优;
值大于1时,代表该决策单元的投入与产出结构处于超级效益模式;
值小于1时,代表该决策单元的投入与产出结构不合理,相对效益未能达到最优,可能存在不同程度的投入冗余和产出不足,其值为技术效益*规模效益。
● 技术效益(technical efficiency, TE)反映的是由于管理和技术等因素影响的生产效率,其值等于1时,代表投入要素得到了充分利用,在给定投入组合的情况下,实现了产出最大化。
● 规模效益(scale efficiency, SE)反映的是由于规模因素影响的生产效率,通常结合规模报酬表进行分析其值等于1时,代表规模效率有效(规模报酬不变),也就是规模适宜,已达到最优的状态;若规模报酬递增(并非其值递增递减或者小于0大于0),代表服务规模过小,需要扩大规模以增加规模效益;若规模报酬递减(并非其值递增递减或者小于0大于0),代表服务规模过大,存在规模过度扩张风险。
● 松驰变量S-(差额变数)指为达到目标效率可以减少的投入量,即非 DEA 有效单元的实际值和目标值之差,
松驰变量S+(超额变数)指为达到目标效率可以增加的产出量,即非 DEA 有效地区的目标值和实际值之差。
● 有效性分析结合综合效益指标,S-和S+共3个指标,可判断DEA有效性,如果综合效益=1且S-与S+均为0,则“DEA强有效”,如果综合效益为1但S-或S+大于0,则“DEA弱有效”,如果综合效益<1则为“非DEA有效”。
4、效益有效性分析
5、规模报酬分析
项 |
规模报酬系数 |
类型 |
1990 |
0.299 |
规模报酬递增 |
1991 |
0.326 |
规模报酬递增 |
1992 |
0.335 |
规模报酬递增 |
1993 |
0.389 |
规模报酬递增 |
1994 |
0.453 |
规模报酬递增 |
1995 |
0.590 |
规模报酬递增 |
1996 |
0.778 |
规模报酬递增 |
1997 |
1.000 |
规模报酬固定 |
1998 |
1.000 |
规模报酬固定 |
1999 |
1.000 |
规模报酬固定 |
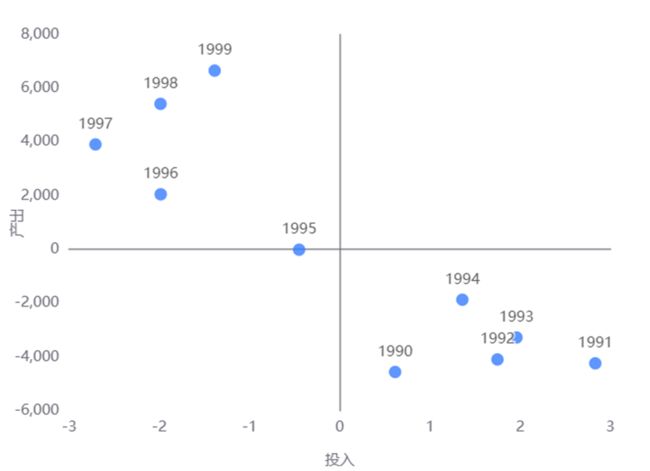
6、象限分析
决策单元 |
投入 |
产出 |
象限分布 |
1990 |
0.614 |
-4560.500 |
第二象限 |
1991 |
2.832 |
-4238.500 |
第二象限 |
1992 |
1.748 |
-4094.830 |
第二象限 |
1993 |
1.959 |
-3276.830 |
第二象限 |
1994 |
1.359 |
-1869.830 |
第二象限 |
1995 |
-0.450 |
-8.170 |
第三象限 |
1996 |
-1.984 |
2054.500 |
第四象限 |
1997 |
-2.707 |
3912.830 |
第四象限 |
1998 |
-1.986 |
5421.830 |
第四象限 |
1999 |
-1.386 |
6659.500 |
第四象限 |
7、投入冗余分析
决策单元 |
松驰变量S-分析 |
投入冗余率 |
|||||
政府财政收入占GDP的比例/% |
环保投资占GDP的比例/% |
每千人科技人员数/人 |
汇总 |
政府财政收入占GDP的比例/% |
环保投资占GDP的比例/% |
每千人科技人员数/人 |
|
1990 |
0.286 |
0.000 |
0.640 |
1.000 |
0.020 |
0.000 |
0.020 |
1991 |
0.586 |
0.000 |
0.000 |
1.000 |
0.035 |
0.000 |
0.000 |
1992 |
0.241 |
0.000 |
0.000 |
0.000 |
0.016 |
0.000 |
0.000 |
1993 |
0.144 |
0.000 |
0.000 |
0.000 |
0.009 |
0.000 |
0.000 |
1994 |
0.322 |
0.000 |
1.850 |
2.000 |
0.023 |
0.000 |
0.057 |
1995 |
1.314 |
0.000 |
4.932 |
6.000 |
0.099 |
0.000 |
0.160 |
1996 |
1.217 |
0.000 |
4.288 |
6.000 |
0.095 |
0.000 |
0.147 |
1997 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1998 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1999 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
投入冗余分析(差额变数分析)主要用于分析各变量需要减少多少投入时才能达目标效率。
● 松驰变量S-(差额变数)指为达到目标效率需要减少的投入量。
● 投入冗余率指“过多投入”与已投入的比值,该值越大意味着“过多投入”越多。
8、产出不足分析
决策单元 |
松驰变量S+分析 |
产出不足率 |
|||
人均GDP/元 |
城市环境质量指数 |
汇总 |
人均GDP/元 |
城市环境质量指数 |
|
1990 |
0.000 |
0.132 |
0.000 |
0.000 |
None |
1991 |
0.000 |
0.054 |
0.000 |
0.000 |
0.599 |
1992 |
0.000 |
0.084 |
0.000 |
0.000 |
1.206 |
1993 |
0.000 |
0.082 |
0.000 |
0.000 |
0.628 |
1994 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1995 |
582.860 |
0.000 |
583.000 |
0.071 |
0.000 |
1996 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1997 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1998 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1999 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
产出不足分析(超额变数分析)主要用于分析各变量需要增加多少产出时达目标效率。
● 松驰变量S-(超额变数)指为达到目标效率可以增加的产出量。
● 产品不足率指“产出不足”与已产出的比值,该值越大意味着“产出不足”越多。
参考资料
浅谈数据包络分析 - 知乎 (zhihu.com)
(5条消息) 数学建模常用模型10 :数据包络(DEA)分析法(投入产出法)_Halosec_Wei的博客-CSDN博客_dea投入产出
数学建模数据包络分析DEA详细教程PPT课件 - 道客巴巴 (doc88.com)