计算机基础--进制转换
计算机基础之进制转换
一、什么叫进制(system)
学习进制转换之前,我们要先知道什么是进制,进制也就是进位计数制,对于任何一种进制——n进制,就表示每一位置上的数运算时都是逢n进一位, 十进制是逢十进一,二进制是逢二进一等,以此类推,n进制就是逢n进一位, n进制的数可以用0~(n-1) 的数表示。
二、常见的进制
- 十进制
逢十进一,用0~9组成。
- 二进制
逢二进一,由 0~1组成。
- 八进制
逢八进一,由 0~7组成。
- 十六进制
十六进制是由 0-9,A-F组成,与十进制对应起来的话就是:0-9 对应 0-9,A-F对应10-15,字母不区分大小写。
三、进制转换本质
[ 进制转换是人们利用符号来计数的方法。进制转换由一组数码符号和两个基本因素“基数”与“位权”构成。基数是指,进位计数制中所采用的数码(数制中用来表示“量”的符号)的个数。位权是指,进位制中每一固定位置对应的单位值。]
这一大段官方解释可能大家看的云里雾里,举个例子:十进制数,他的进制基数就是十,或者你可以这样记,进制基数等于第一位数的位权值,十进制数第零位数的位权值为10的0次方(个位),第一位数的位权值为10的1次方(十位),第三位数的位权值为10的2次方(百位),以此类推。
1024=1×1000+0×100+2×10+4×1
四、进制的转换公式
1.二进制转换十进制
二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……
设有一个二进制数:1000001001,转换为10进制为:
竖式:
从右往左开始换算
第0位 1×2的0次方 = 1
第1位 0×2的1次方 = 0
第2位 0×2的2次方 = 0
第3位 1×2的3次方 = 8
第4位 0×2的4次方 = 0
第5位 0×2的5次方 = 0
第6位 0×2的6次方 = 0
第7位 0×2的7次方 = 0
第8位 0×2的8次方 = 0
第9位 1×2的9次方 = 512
除0以外的数字0次方都是1,但0乘以多少都是0,所以我们可以直接跳过值为0的位:
1×2的0次方 + 1×2的3次方 + 1×2的9次方 = 51 内蒙红色教育培训 www.xjganxun.cn 2
2.八进制转换十进制
八进制数 逢八进一,采用 0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……
设有一个八进制数:1111,转换为10进制为:
竖式:
第0位 1×8的0次方 =1
第1位 1×8的1次方 = 8
第2位 1×8的2次方 = 64
第3位 1×8的3次方 = 512
得数:565
3.十六进制转换十进制
十六进制逢十六进一,0-9对应0-9,A-F对应10-15,字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
在第N (N从0开始) 位上,如果是数 x (x大于等于0,且x小于等于15,即:F)表示的大小为 x × 16 的N次方。
设有一个八进制数: 2AF5, 转换为10进制为:
竖式:
第0位: 5 × 16的0次方 = 5
第1位: F × 16的0次方 = 240
第2位: A × 16的0次方 = 2560
第3位: 2 × 16的0次方 = 8192
得数: 10997
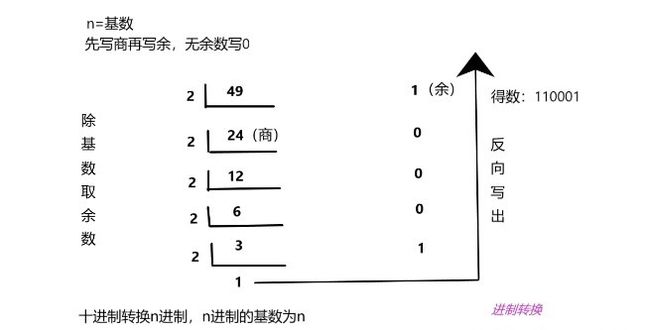
4.十进制转换其他进制
以此类推十进制转换其他进制
5.八进制与二进制的转换
二进制到八进制
以11 001为例:
整数部分:从后往前每三位一组,缺位处用0填补,然后按十进制方法进行转化, 则:
001=1
011=3
然后我们将结果按从下往上的顺序书写就是:31,那么这个31就是二进制11001的八进制形式
八进制到二进制
以31为例:
整数部分:从后往前每一位按十进制转化方式转化为三位二进制数,缺位处用0补充 则:
1---->001
3---->011
然后我们将结果按从下往上的顺序书写就是:11001,那么这个11001就是八进制31的二进制形式
6.十六进制与二进制的转换
我们先看一张表
由于1111才4位,所以我们直接记住它每一位的权值,并且是从高位往低位记:8、4、2、1。
记住8421,对于任意一个4位的二进制数,我们都可以很快算出它对应的10进制值。
二进制整数转换为十六进制整数时,每四位二进制数字转换为一位十六进制数字,运算的顺序是从低位向高位依次进行,高位不足四位用零补齐,参考上表,我们很快就能得出答案。
十六进制整数转换为二进制整数时,思路是相反的,每一位十六进制数字转换为四位二进制数字,运算的顺序也是从低位向高位依次进行,举个例子:看到F之后,我们需知道它是15,然后15如何用8421拼凑呢,应该是8 + 4 + 2 + 1,所以为11111。
结尾
本文只记录了基本进制之间的相互转换,由于在C语言编程中二进制、八进制、十六进制之间几乎不会涉及小数的转换,所以这里只讲整数的转换,并且八进制和十六进制之间极少直接转换,这里也不再讲解,如果想了解更多,可以自己搜索一些材料,另外,转换方法是通用的,任何进制之间的转换都可以采用。