python数据分析 - 如何探索数据

1.数据的组成

数据的来源非常丰富，数据大类分为非结构化、结构化，矩形数据（也就是pandas常见的series和dataframe）和非矩形数据

1.1 非结构化数据

例如传感器的测量值，事件，文本、图像和视频等。都是非结构化的

• 图像由一系列像素点组成，每个像素包括了红、绿、蓝三原色信息；
• 文本是单词和非单词字符的序列，常以章节、子章节 等形式组织在一起；
• 点击流是用户在App 或Web 页面上的动作序列。

1.2 结构化数据

结构化数据有基本二种类型，即数值型数据和分类数
数值型数据有连续型和离散型两种形式

• 风速、持续时间等是连续型数据
• 某一事件的发生次数则是离散型数据

分类数据只能取一系列固定的值，分类数据有二种特殊的形式有二元数据和有序数据

• 例如，电视屏幕的类型可以是等离子体、LCD 或LED 等，美国各州的名称包括阿拉巴马州、阿拉斯加州等。
• 二元数据是一种重要且特殊的分类数据，该类数据的取值只在两者中择其一，例如0 或1、是或否、True 或False 等。
• 有序数据是另一种有 用的分类数据，该类数据是按分类排序的，例如数值排序（1、2、3、4 或5）

1.3 矩形数据

矩形数据对象包括电子表格、数据库表等，其中在我们实际运用中最常见就是pandas的series和dataframe数据结构。通常一个数据有多个特征，每个特征就包含我们的结构化数据。
$$结构化数据\in 矩形数据$$

1.4 非矩形数据

除了矩形数据之外，还有一些其他类型的数据

• 时序数据记录了对同一变量的连续测量值。它是统计预测方法的原始输入数据，也是物联网设备所生成的数据的关键组成部分。
• 空间数据结构用于地图和定位分析，它比矩形数据结构更为复杂和多变。在对象表示中，空间数据关注的是对象（例如一所房子）及其空间坐标。与之形成对比的是，字段视图关注空间中的小单元及相关的度量值（例如像素点的亮度）。
• 图形（或网络）数据结构用于表示物理上的、社交网络上的和抽象的关系。例如，Facebook 或LinkedIn 等社交网络图表示了人们在网络上的相互联系

2.位置估计

估计量是用来描述所看到的数据情况与确切的（或理论上为真的）状态之间的差异。

探索数据的一个基本步骤，就是获得每个特征（变量）的“典型值”。典型值是对数据最常出现位置的估计，即数据的集中趋势。

主要包含的位置估计参数有：

• 均值：所有数据值之和除以数值的个数
• 加权均值：各数值乘以相应的权重值，然后加总求和，再除以权重的总和
• 中位数：使得数据集中分别有一半数据位于该值之上和之下
• 加权中位数：使得排序数据集中分别有一半的权重之和位于该值之上和之下
• 切尾均值：在数据集剔除一定数量的极值后，再求均值
• 稳健：对极值不敏感
• 离群值：与大部分数据值差异很大的数据值

2.1 均值

均值
均值，又称平均值，是最基本的位置估计量。均值等于所有值的总和除以值的个数。
$$均值=\overline{x}=\frac{{\sum }_i^n{x}_i}{n}$$

切尾均值
切尾均值是均值的一个变体。计算切尾均值时，需要在一个有序数据集的两端上去除一定数量的值，再计算剩余数值的均值

$$切尾均值=\overline{x}=\frac{{\sum }_{i=p+1}^{n-p}{x}_i}{n-2p}$$

举个例子，在国际跳水比赛中，会有五名裁判打分，一名选手的最终得分需要去除其中的最高分和最低分，取余下三名裁判打分的均值

加权均值
在计算加权均值时，要将每个值xi 乘以一个权重值wi，并将加权值的总和除以权重的总和。计算公式为：
$$加权均值={\overline{x}}_w=\frac{{\sum }_{i=1}^n{w}_i{x}_i}{{\sum }_i^n{w}_i}$$

使用加权均值，主要是出于以下两个方面的考虑。

• 一些值本质上要比其他的值更为多变，因此需要对多变的观测值赋予较低的权重。例如，如果我们需要对来自多个传感器的数据计算均值，但是其中一个传感器的数据不是很准确，那么我们可对该传感器的数据赋予较低的权重。
• 所采集的数据可能并未准确地表示我们想要测量的不同群组。例如，受限于在线实验的开展方式，我们得到的数据集可能并未准确地反映出不同用户群组的情况。为了修正这一问题，我们可对未准确表示的群组赋予较高的权重。

2.2 中位数和稳健估计量

中位数
考虑到均值对数据的敏感性，比如说互联网大厂的人均收入，底层大量的员工的收入被高层少量的收入，拉平均了。因此在不少实际应用中，中位数依然是更好的位置度量。

加权中位数
有时我们需要计算加权中位数，这与使用加权均值的原因相同。和计算中位数一样，我们首先不考虑每个数值所关联的权重，对数据集排序。取可以使有序数据集上下两部分的权重总和相同的值。和中位数一样，加权中位数也对离群值不敏感

离群值
我们称中位数为一种对位置的稳健估计量，因为它不会受离群值（极端情况）的影响，而离群值会使结果产生偏差。离群值是距离数据集中其他所有值都很远的值，在普通数据分析中，离群值处理使用异常检测，来测定异常。

3.变异性估计

位置只是总结特性的一个维度，另一个维度是变异性（variability），也称离差（dispersion），它测量了数据值是紧密聚集的还是发散的。

变异性是统计学的一个核心概念，统计学关注如何测量变异性，如何降低变异性，如何识别真实变异性中的随机性，如何识别真实变异性的各种来源。

主要包含的变异性估计参数有：

• 偏差：位置的观测值与估计值间的直接差异
• 方差：对于n 个数据值，方差是对距离均值的偏差平方后求和，再除以n-1
• 标准偏差：方差的平方根
• 平均绝对偏差：对数据值与均值间偏差的绝对值计算均值
• 中位数绝对偏差：数据值与中位数间绝对偏差的均值
• 极差：数据集中最大值和最小值间的差值
• 顺序统计量：基于从大到小排序的数据值的度量
• 百分位数：表示一个数据集中，P% 的值小于或等于第P 百分位数，(100−P)% 的值大于或等于第P 百分位数
• 四分位距：第75 百分位数和第25 百分位数间的差值

3.1 标准偏差及相关估计值

使用最广泛的变异性估计量基于位置估计值和观测数据值间的差异或偏差。给定一个数据集{1, 4, 4}，其均值是3，中位数是4。各个数据与均值的偏差分别为：1−3 = −2，4−3 = 1，4−3 = 1。这些偏差值说明了数据围绕中心值的分散程度。

一种测量变异性的方法是，估计这些偏差的一个典型值。然而，对这些偏差值本身取均值是无法给出更多信息的，因为负的偏差值将会抵消正的偏差值。事实上，相对于均值的偏差值的总和为零。一种简单的方法是对均值偏差的绝对值取均值。在上例中，各偏差的绝对值分别是2、1 和1，它们的均值为(2 + 1 + 1)/3 = 1.33。这就是平均绝对偏差，计算公式为：
$$平均绝对偏差=\frac{{\sum }_{i=1}^n|x_i-\overline{x}|}{n}$$

其中x 是样本的均值。
最广为人知的变异性估计量是方差和标准偏差，它们基于偏差的平方。方差是偏差平方值的均值，而标准偏差是方差的平方根。

$$方差=S^2=\frac{\sum (x-{\overline{x}}^2)}{n-1}$$
$$标准偏差=s=\sqrt{\frac{\sum (x-{\overline{x}}^2)}{n-1}}$$
标准偏差比方差更易于理解，因为它具有与原始数据相同的尺度

自由度是n，还是n-1
如果在方差公式中使用了直观的除数n，那么就会低估方差的真实值和总体的标准偏差。这被称为有偏估计。但是，如果除以n−1 而不是n，这时标准偏差就是无偏估计。

总结
无论方差、标准偏差，还是平均绝对偏差，它们对离群值和极值都是不稳健的。其中，方差和标准偏差对离群值尤为敏感

但是中位数绝对偏差（MAD）是一种稳健的变异性估计量。中位数绝对偏差的计算公式为：

$$MAD=中位数(|x_1-m|,|x_2-m|,...,|x_n-m|)$$
其中，m 是中位数。和中位数一样，中位数绝对偏差也不受极值的影响。我们可以参考切尾均值的计算方法，计算切尾标准偏差。

3.2 基于百分位数的估计量

另一种估计离差的方法基于对有序数据分布情况的查看。基于有序数据的统计量被称为顺序统计量，其中最基本的测量是极差，即数据的最大值与最小值之间的差值。知道最大值和最小值本身也是十分有用的，这有助于识别离群值。但是极差对离群值非常敏感，对于测量数据的离差并非十分有用。

为避免对离群值敏感，我们可以删除有序数据两端的值，然后再查看数据的极差。正式表述为，此估计量基于百分位数间的差异。在一个数据集中，第P 百分位数表明，至少有P% 的值小于或等于该值，而(100−P)% 的值大于或等于该值。

例如，如果要找到第80 百分位数，我们首先对数据进行排序，然后从最小值开始，按照从小到大的顺序数出其中80% 的数值。注意，中位数等同于第50 百分位数。百分位数在本质上等同于四分位数，
而四分位数是根据分数做索引的，因此0.8 四分位数等同于第80 百分位数

4.数据分布

前文介绍的各种估计量都是通过将数据总结为单一数值，去描述数据的位置或变异性。这些估计量可用于探索数据的整体分布情况。

主要包含的数据分布方法有：

• c图基提出的一种绘图，是一种快速可视化数据分布情况的方法
• 频数表：将数值型数据的计数情况置于一组间隔（组距）中
• 直方图：对频数表的绘图，其中x 轴是组距，y 轴是计数（或比例）
• 密度图：直方图的平滑表示，通常基于某种核密度估计

4.1 百分位数和箱型图

箱子的顶部和底部分别是第75 百分位数和第25 百分位数。箱内的水平线表示的是中位数。图中的虚线称为须（whisker）。须从最大值一直延伸到最小值，显示了数据的极差

4.2 频数表和直方图

变量的频数表将该变量的极差均匀地分割为多个等距分段，并给出落在每个分段中的数值个数。

例子：
根据上海4月1日到4月11日，每日新增无症状数据为例：

时间	每日新增无症状
4.1	6051
4.2	7788
4.3	8581
4.4	13086
4.5	16766
4.6	19660
4.7	20398
4.8	22609
4.9	23937
4.10	25173
4.11	22348

• 新增无症状人数最大的是4.10号，人数最少的是4.1号 极差为25173-6051=19122
• 我们将极差划分成大小相等的组距，假定为10个组距，这样每个组距宽度为1912.2。
• 第一个组距的范围是从6051到7963.2，最后一个组距范围是从23260.8到25173

直方图是频数表的一种可视化方法，其中x 轴为组距，y 轴为数据的计数。

在绘制直方图时应注意以下几点：

• 空组距也应包括在直方图中。
• 各组距是等宽的。
• 组距的数量（或组距的大小）取决于用户。
• 各条块相互紧挨着，条块间没有任何空隙，除非存在空组距。

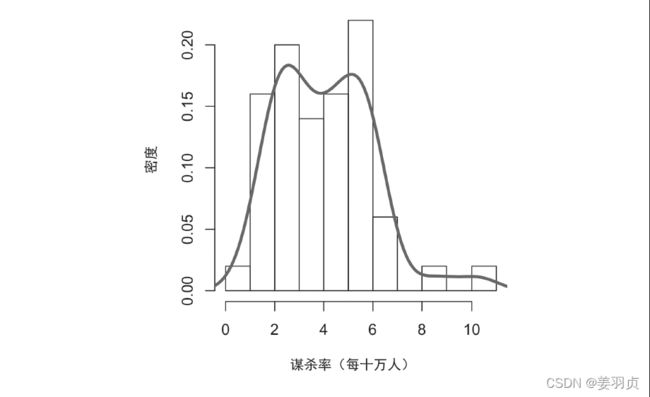
4.3 密度估计

密度图与直方图有关，它用一条连续的线显示数据值的分布情况。我们可以将密度图看作由直方图平滑得到的

总结

• 频数直方图在y 轴上绘制频数计数，在x 轴上绘制变量值。它提供了对数据分布的概览。
• 频数表是直方图中频数计数的表格形式。
• 在箱线图中，箱子的顶部和底部分别表示第75 百分位数和第25 百分位数。箱线图也提供了数据分布的基本情况。多个箱线图通常是并排展示的，以便于比较分布情况。
• 密度图是直方图的一种平滑表示。它需要一个基于数据估计绘图的函数（当然也可以做多个估计）。

4.4 二元数据和分类数据

使用基本的比例或百分比，我们就能了解分类数据的情况

主要包含的分类数据情况的参数有：

• 众数：数据集中出现次数最多的类别或值
• 期望值：如果类别可以与一个数值相关联，可以根据类别的出现概率计算一个平均值
• 条形图：在绘图中，以条形表示每个类别出现的频数或占比情况
• 饼图：在绘图中，圆饼中的一个扇形部分表示每个类别出现的频数或占比情况

4.4.1 众数

众数指数据中出现最频繁的一个或一组数值

4.4.2 期望值

分类数据还有一个特殊类型，即数据类别可以表示成（或映射到）同一尺度的离散值。

例如
新兴云技术的服务商提供了两种服务，一种服务的费用为每月300 美元，另一种为每月50 美元。服务商会举办免费的网络研讨会，以发现一些潜在的用户。来自企业的数据表明，有5% 的研讨会参与者将会注册每月300 美元的服务，15% 的参与者会注册每月50美元的服务，另外80% 的人将不会注册任何服务。

这样，我们可以将数据总结为一个期望值，估计企业的营业收入。期望值是一种加权均值，权重使用的是类别出现的概率。

期望值的计算方法如下

1. 输出值乘以其出现的概率。
2. 将这些值加起来。

就上面给出的云服务例子而言，与会者支付服务费的期望值是每月22.5 美元，计算过程如下。
$$期望值=0.05\times 300+0.15\times 50+0.80\times 0=22.5$$
期望值实际上是一种加权均值，其中加入了未来期望和概率权重的概念，所使用的概率。

通常是根据主观判断得到的。期望值是商业估值和资金预算中的一个基本概念，

例如：一次新收购在未来5 年中利润的期望值，或者一个诊所的新患者管理软件在节约开支上的期望值。

5.相关性

无论是在数据科学还是研究中，很多建模项目的探索性数据分析都要检查预测因子之间的相关性，以及预测因子和目标变量之间的相关性。给定变量X 和Y，它们均有测量数据。

如果变量X 的高值随变量Y 的高值的变化而变化，并且X 的低值随Y 的低值的变化而变化，那么我们称X 和Y 是正相关的。如果X 的高值随Y 的低值的变化而变化，反之亦然，那么我们称变量X 和Y 是负相关的

主要描述相关性的参数有：

• 相关系数：一种用于测量数值变量间相关程度的度量，取值范围在−1 到+1 之间
• 相关矩阵：将变量在一个表格中按行和列显示，表格中每个单元格的值是对应变量间的相关性
• 散点图：在绘图中，x 轴显示一个变量的值，y 轴显示另一个变量的值

5.1 相关系数

考虑下面两个变量v1 和v2。它们是完全相关的，因为每个变量中的观测值都是按从小到大排列的。
$v1:1,2,3$
$v2:4,5,6$
向量点积是4 + 10 + 18 = 32。现在我们尝试将其中一个变量中的观测值随机重排，然后重新计算二者的点积，所得到的值永远不会大于32。因此，我们可以将向量点积作为一个度量，即做任意次随机排序后，向量点积都不会大于32。（事实上，这一理念是与基于重抽样的估计密切相关的，参见3.1 节。）尽管如此，该度量值并非很有意义，除非用于重抽样分布。

点积的一种标准化变体就是相关系数，该度量更为有用。对于两个总是保持同一尺度的变量，相关系数给出了两者间相关性的估计值。在计算皮尔逊相关系数时，要将变量v1 的平均偏差乘以变量v2 的平均偏差，再除以标准偏差之积，计算公式如下。
$$r=\frac{{\sum }_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{(n-1)S_x{S}_y}$$

注意，公式中使用的除数是n−1，而不是n。相关系数的值总是位于+1（完全正相关）和−1（完全负相关）之间。0 表示没有相关性

5.2 相关矩阵

如下图电信类股票收益间的相关性：

它显示了自2012 年7 月到2015 年6 月间的电信类股票每日收益间的相关性。从中可以看到，股票Verizon（VZ）与ATT（T）间的相关性最高，而与通信基础设施运营企业Level Three（LVLT）间的相关性最低。需要注意的是，相关矩阵的对角线元素为1（即一支股票与其自身的相关性是1），并且对角线上下对称位置的信息是冗余的

也可以转化为图的样式：

5.3 散点图

散点图是一种可视化两个测量数据变量间关系的标准方法。在散点图中，x 轴表示一个变量，y 轴表示另一个变量，图中的每个点对应于一条记录。

从图中可以看到，两支股票的日收益具有强正相关性。在大部分交易日中，两支股票都保持同步涨跌。但还有少数几个交易日，其中一支股票明显下跌而另一支股票上涨，或是相反

6.多变量分析

上面介绍的估计量都是我们熟知的，比如均值和方差。计算这些估计量时，我们一次仅查看一个变量，这被称为单变量分析。而相关性分析是比较两个变量间关系的一种重要方法，这是双变量分析。本节将介绍一些包含两个及以上变量的估计量及绘图，即多变量分析。

6.1 六边形图和等势线（适用于两个数值型变量）

六边形：如下图所示：

它显示了金县的房屋面积（平方英尺）与纳税评估值间的关系。六边形图绘制的并非数据点，这样会导致图中显示成一片黑云，我们将记录分组为六边形的组距，并用不同的颜色绘制各个六边形，以显示每组中的记录数。

在图中可清晰地看到，房屋面积（平方英尺）和纳税评估值间是正相关的。图中值得关注的一个特征是，在主要云上，隐含有另一片云。这片云所表示的房屋虽然与主要云所表示的房屋具有相同的面积，但是纳税评估值更高

等势线：如下图所示

每条等势线表示特定的密度值，并随着接近“顶峰”而
增大

6.2 多个变量的可视化

比较两个变量所用的图表类型，例如散点图、六边形图和箱线图，完全可以通过条件（conditioning）这一概念扩展到多个变量。