广度优先遍历

思想概述

广度优先搜索（Breadth_First_Search），又称广度优先搜索，简称BFS

现有一把钥匙丢在家里需要寻找，如果说深度优先搜索是把家中每个房间按顺序都彻底搜查一遍，例如先把卧室的桌子柜子抽屉床底下甚至是衣柜顶都找一遍，然后再去厨房仔细搜索还是没有再去厕所，最后在厕所的洗手台上找到了，那么这个时候显然用深度搜索是不合理的，如果一开始只是把每个房间都简单的搜查一遍那么很快就能在洗手台上找到钥匙

那么广度优先搜索就是先把每个房间显眼的地方先搜查一遍，如果没有找到再把每个房间比较常用的家具附近查找一遍。如果还是没有找到再把每个房间的柜子抽屉都翻开查找，如果还是没有找到再把每个房间的床底下衣柜上方等都仔仔细细查找一遍，这样一遍遍的加大查找的范围，直到找到为止这就是广度优先搜索

我们将这种思想化为图来看一看

这是一张无向图

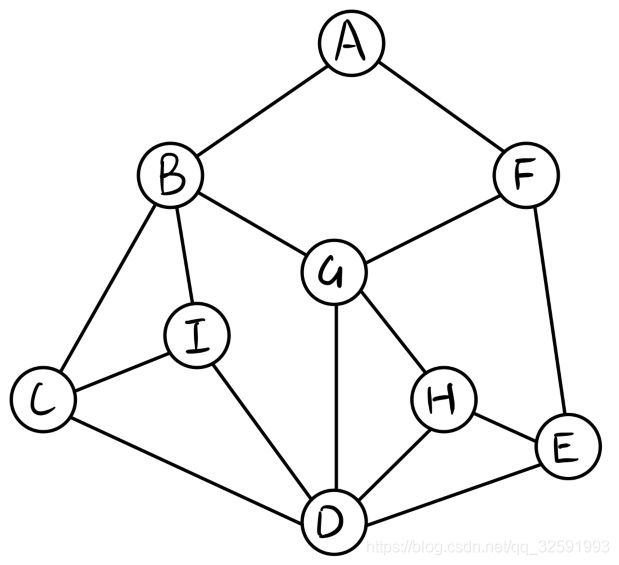
我们将这张图稍微变形一下

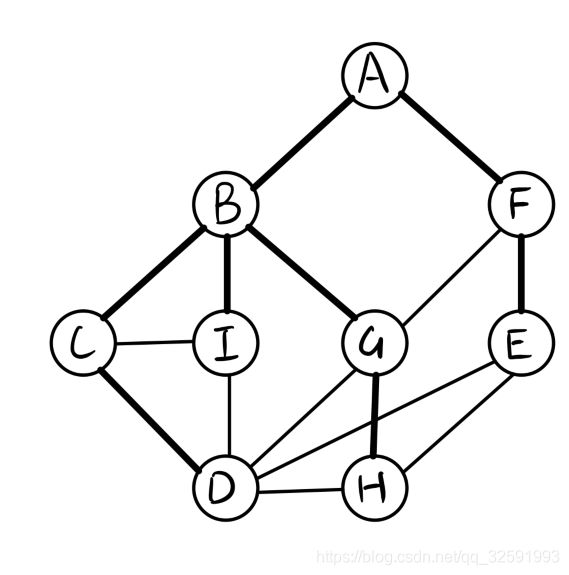
结点由上至下层次分明
我们将第一层的结点取出放入一个队列中

A

再将A结点的邻接点全部放入队列中，并将A移出队列

B F

再将B结点的邻接点全部放入队列中，并将B移出队列

F C I G

再将F结点的邻接点全部放入队列中，并将F移出队列

C I G E

再将C结点的邻接点全部放入队列中，并将C移出队列

I G E D

再将I结点的邻接点全部放入队列中，并将I移出队列

G E D

再将G结点的邻接点全部放入队列中，并将G移出队列

E D H

再将E结点的邻接点全部放入队列中，并将E移出队列

D H

再将D结点的邻接点全部放入队列中，并将D移出队列

H

这是这个队列完整的状态（从左出队列从右进队列）

<-- A       <--
<-- B F     <--
<-- F C I G <--
<-- C I G E <--
<-- I G E D <--
<-- G E D   <--
<-- E D H   <--
<-- D H     <--
<-- H       <--

样例代码：

import java.util.LinkedList;
import java.util.Queue;

public class Test {
	// 构造图的邻接矩阵
    private static int[][] edges = { 
    		{ 0, 1, 0, 0, 0, 1, 0, 0, 0 },
            { 1, 0, 1, 0, 0, 0, 1, 0, 1 }, 
            { 0, 1, 0, 1, 0, 0, 0, 0, 1 },
            { 0, 0, 1, 0, 1, 0, 1, 1, 1 }, 
            { 0, 0, 0, 1, 0, 1, 0, 1, 0 },
            { 1, 0, 0, 0, 1, 0, 1, 0, 0 }, 
            { 0, 1, 0, 1, 0, 1, 0, 1, 0 },
            { 0, 0, 0, 1, 1, 0, 1, 0, 0 }, 
            { 0, 1, 1, 1, 0, 0, 0, 0, 0 } };
    // 构造图的结点
    private static String[] vertexs = { "A", "B", "C", "D", "E", "F", "G", "H", "I" };
    // 结点个数
    private static int vertexsNum = vertexs.length;
    // 记录结点是否被访问
    private static boolean[] visit = new boolean[vertexsNum];
    
	// 广搜
	public static void BFS() {
		Queue<Integer> queue = new LinkedList<Integer>();	// 创建队列
		queue.offer(0);		// 先把第一个结点放入队列
		visit[0]=true;		// 标记这个结点为已访问
		while(!queue.isEmpty()) {	// 只要队列不为空,就一直执行下面的操作
			int next=queue.poll();	// 从队列里取出来一个结点
			System.out.print(vertexs[next]+" ");	// 对这个结点进行操作,这里是输出这个结点
			for(int j=0;j<vertexsNum;j++) {			// 循环将这个结点所有的邻近结点都放入队列中
				if(edges[next][j]==1 && !visit[j]) {	//如果这个邻近结点已被访问那么就不放进去
					queue.offer(j);					// 入队
					visit[j]=true;					// 标记已访问
				}
			}
		}
	}
	
	public static void main(String[] args) {
		BFS();
	}
}