红黑树详解（C/C++实现）

红黑树的用途非常广泛，像在map\epoll\定时器\Nginx\CFS\内存管理中都使用了红黑树对节点进行管理

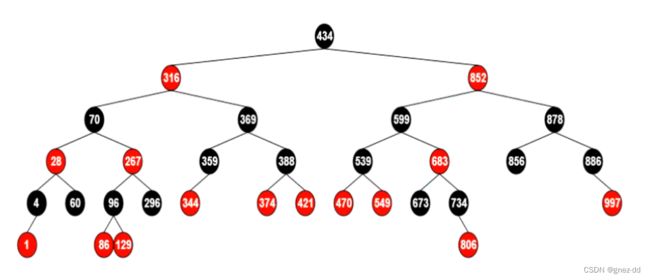
红黑树是一颗接近平衡的二叉搜索树，没有AVL树的平衡因子概念，只是靠满足五条性质维持接近平衡的结构，保证最长路径不超过最短路径的2倍

适用于需要排序的场景下，红黑树不需要像二叉搜索树在极端情况下形成链表导致O(n)的时间复杂度，又不需要像平衡搜索树在维持树的平衡上面过多的性能消耗

性质

• 节点是红色或者黑色的

• 根是黑色的

• 叶子节点都是黑色（叶子节点是指最底层的空节点，null节点）

• 红节点的子节点都是黑色的

  • 红节点的父节点是黑色的

  • 从根节点到叶子节点的路径上不会存在两个连续的红节点

• 从任意节点到其每个叶子节点的所有路径都包含相同数目的黑节点

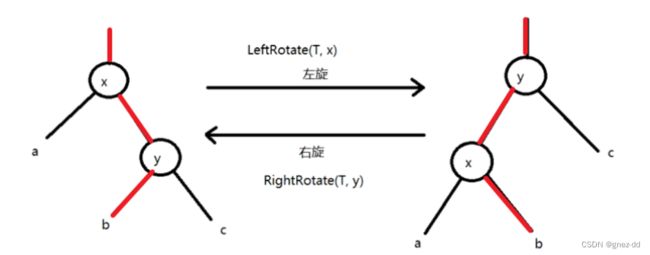
左旋右旋

左旋：

• 将y原来的左子树接到x的右子树下

• 将y的父节点指向x的父节点，x的父节点原来指向x改为指向y

• 将x接到y的左子树节点下

右旋：

• 将x原来的右子树接到y的左子树下
• 将x的父节点指向y的父节点，y的父节点原来指向y改为指向x
• 将y接到x的右子树节点下

代码实现

// 左旋
void leftRotate(RbTree *T, RbTreeNode *x) {
    RbTreeNode *y = x->right;

    // 1.将y原来的左子树接到x的右子树下
    x->right = y->left;
    if (y->left != T->nil) {
        y->left->parent = x;
    }

    // 2.将y的父节点指向x的父节点,x的父节点原来指向x改为指向y
    y->parent = x->parent;
    if (x->parent == T->nil) {
        // 此时Y是根节点
        T->root = y;
    } else if (x == x->parent->left) {
        x->parent->left = y;
    } else {
        x->parent->right = y;
    }

    // 3.将x接到y的左子树下
    y->left = x;
    x->parent = y;
}

// 右旋
void rightRotate (RbTree *T, RbTreeNode *y) {
    RbTreeNode* x = y->left;

    // 1.将x原来的右子树接到y的左子树下
    y->left = x->right;
    if (x->right != T->nil) {
        x->right->parent = y;
    }

    // 2.将x的父节点指向y的父节点，y的父节点原来指向y改为指向x
    x->parent = y->parent;
    if (y->parent == T->nil) {
        T->root = x;
    } else if (y->parent->left == y) {
        y->parent->left = x;
    } else {
        y->parent->right = x;
    }

    // 3.将y接到x的右子树下
    x->right = y;
    y->parent = x;
}

左旋右旋的代码中只不过left和right交换，x和y交换，其他都一样

增加节点

全部都添加到叶子节点中，最后再去调整

增加的节点默认是红色的，不会去影响路径上黑色节点的数量

原因：避免每一次加入都需要去旋转

void rbTreeInsert(RbTree *T, RbTreeNode *newNode) {
    RbTreeNode* node = T->root;
    RbTreeNode* parent = T->nil;

    // 寻找可以插入的位置 找到叶子节点
    while (node != T->nil) {
        parent = node;
        if (newNode->key < node->key) {
            node = node->left
        } else if (newNode->key > node->key) {
            node = node->right;
        } else {
            return; // 具体相同的值要不要改动看需求
        }
    }

    newNode->parent = parent;
    if (parent == T->nil) {
        T->root = newNode;
    } else if (parent->key > newNode->key) {
        parent->left = newNode;
    } else {
        parent->right = newNode;
    }
    newNode->left = T->nil;
    newNode->right = T->nil;
    newNode->color = RED;

    rbTreeInsertFixup(T,newNode);
}

树的调整

当父节点为红色节点的时候就需要调整，因为违反了规则四

调整的过程中会遇到三种情况：

• 叔父节点是红色
• 叔父节点是黑色，当前节点父节点是左子树
• 叔父节点是黑色，当前节点父节点是右子树

如果叔父节点是红色那么在左右不需要区分，没有什么区别，到时候祖父节点改为红色，父节点和叔父节点改为黑色继续向上调整

但是如果是黑色就需要区分了，因为父节点和祖父节点颜色的时候会导致黑色路径高度发生变化

目前已知的情况：

• 当前节点是红色
• 父节点是红色
• 祖父节点是黑色

叔父节点是红色的

将父亲和叔父都改为黑色，此时黑色路径长度发生变化，需要将祖父改为红色

从祖父开始继续向上调整

父亲是祖父的左孩子

自己是父亲的左孩子：

将父亲变为黑色，此时左边黑色路径发生变化，需要将祖父改为红色

此时右子树黑色路径减少，需要对祖父右旋，将父节点成为新祖父恢复右子树的黑色高度

自己是父亲的右孩子：

将父亲左旋变为父亲是自己的左孩子，就变成上面的情况了

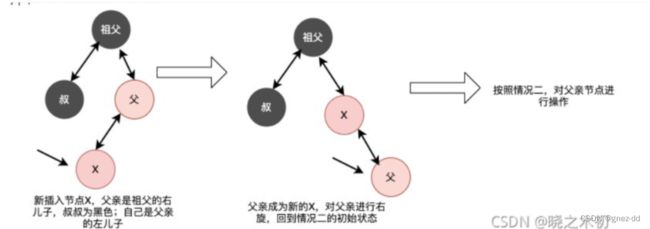
父亲是祖父的右孩子

自己是父亲的右孩子：

将父亲变为黑色，此时右边黑色路径变长，将祖父变为红色

此时左边黑色路径变短，进行左旋恢复左子树高度

自己是父亲的左孩子：

对父亲进行右旋让父亲成为自己的右孩子变成上面的情况

// 调整树
void rbTreeInsertFixup(RbTree *T, RbTreeNode *node) {
    // 如果父节点是黑色的则不需要调整
    while (node->parent->color == RED) {
        // 父节点是祖父节点的左子树
        if (node->parent == node->parent->parent->left) {
            // 叔父节点
            RbTreeNode *uncle = node->parent->parent->right;
            if (uncle->color == RED) {
                // 将父节点改为黑色和叔父节点改为黑色，祖父节点改为红色继续向上调整就可以了
                // 会影响到黑色路径的长度
                node->parent->color = BLACK;
                uncle->color = BLACK;
                node->parent->parent->color = RED;
                // 继续向上调整
                node = node->parent->parent;
            } else {
                if (node == node->parent->right) {
                    // 左旋
                    node = node->parent;
                    leftRotate(T,node);
                }
                // 让父节点变为黑色，祖父节点变为红色（右子树的黑色高度变低了）
                // 对祖父右旋，让父节点成为新祖父，恢复右子树的高度
                // 这种情况只需要两次旋转就可以完成调整了
                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                rightRotate(T,node->parent->parent);
            }
        } else {
            RbTreeNode *uncle = node->parent->parent->left;
            if (uncle->color == RED) {
                node->parent->color = BLACK;
                uncle->color = BLACK;
                node->parent->parent->color = RED;
                node = node->parent->parent;
            } else {
                if (node == node->parent->left) {
                    node = node->parent;
                    rightRotate(T,node);
                }
                // 左子树的高度减小了
                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                leftRotate(T,node->parent->parent);
            }
        }
    }

    T->root->color = BLACK;
}

删除节点

定义三种节点：

• 覆盖节点Z：被指定删除的结点，实际上是通过被覆盖实现
• 删除节点Y：实际上被删除的节点，一般是后继节点
• 轴心节点X：维护红黑树的节点

删除的节点可能有三种情况：

• 没有左右子树：直接删除
• 有且只有一颗子树：将该节点的唯一子树挂到父节点上，然后删除该节点
• 左右子树都有：找一个后继节点Y覆盖指定节点Z，然后删除节点Y，Y是情况1或2中的一种

如果当前结点是父结点的左子树的情况，可以归纳出来四种情况。同理如果当前结点是父结点的右子树，我们也可以归纳出来四种情况。但是这四种情况的差异就是旋转方向的区别而已（镜像的）。一共是8种情况，但是归纳出来其实是4种

当前节点是父节点的左子树

情况一：当前节点的兄弟节点是红色

将兄弟变为黑色，父亲变为红色，此时左边高度降低，对父节点左旋恢复左子树高度，此时兄弟的左孩子变为新的兄弟，变为情况2、3、4

（因为要让x的兄弟是黑色，所以只能从左右侄子中获得）

情况二：兄弟为黑色，左右侄子也是黑色

此时兄弟和自己都是黑色，父节点为红色或黑色

将兄弟变为红色，轴心节点变为父节点（原来的轴心节点所在路径少了一个黑色节点，所以将兄弟变为红色，此时父节点的黑色路径是相同的了，但是父节点之上的路径少了一个黑色节点，所以将轴心节点变为父节点，继续调整）

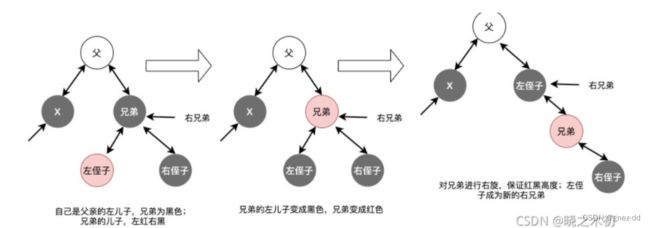
情况三：兄弟是黑色，右侄子是黑色，左侄子是红色

将左侄子变为黑色，兄弟变为红色，此时右子树黑色高度降低，对兄弟节点继续右旋恢复高度，此时左侄子成为新的右兄弟

此时兄弟的右儿子是红色，符合情况4，按照情况4的方法继续调整

情况四：兄弟是黑色，右侄子是红色，左侄子是红色或黑色

将兄弟颜色改为和父节一样，右侄子和父节点都变为黑色

为了保证父节点变为黑色后高度不变需要将父节点左旋

x指向根节点，循环结束

为什么要将右侄子变为黑色：因为经过左旋后右侄子变为新的兄弟，代替了原来的兄弟，所以需要变为和兄弟颜色一样，也就是黑色

为什么要将兄弟变为和父节点一样：因为经过左旋后兄弟代替了父节点

为什么要将父节点变为黑色：因为父节点左旋弥补了被删除的黑色节点

此时路径恢复了

当前节点是父节点的右子树

和上面的情况一样，是镜像的

总结

会有两种情况导致循环退出不再需要调整：

情况二的时候轴心节点变为父节点，如果父节点是红色那么就可以退出将父节点改为黑色就可以恢复高度了

情况四：通过使用父节点弥补被删除节点恢复高度，最后再将轴心节点置为根节点退出循环

每一种情况都是尽可能向第四种情况靠近，实现兄弟是黑色，右侄子是红色的情况

代码

// 寻找x节点的最左节点
RbTreeNode* rbTree_mini(RbTree *T, RbTreeNode *x) {
    while (x->left != T->nil) {
        x = x->left;
    }
    return x;
}

// 寻找覆盖节点的右子树的最左节点
RbTreeNode* rbTree_successor(RbTree *T, RbTreeNode* x) {
    RbTreeNode *y = x->parent;

    // 寻找x节点的右子树的最左节点
    if (x->right != T->nil) {
        return rbTree_mini(T,x->right);
    }
}

void rbTree_delete_fixup(RbTree *T, RbTreeNode* x) {
    while ((x != T->root) && (x->color == BLACK)) {
        if (x == x->parent->left) {
            // w为兄弟节点
            RbTreeNode *w = x->parent->right;
            if (w->color == RED) {
                w->color = BLACK;
                x->parent->color = RED;
                leftRotate(T,x->parent);
                w = x->parent->right;
            }
            if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
                w->color = RED;
                x = x->parent;
            } else {
                if (w->right->color == BLACK) {
                    w->left->color = BLACK;
                    w->color = RED;
                    rightRotate(T,w);
                    w = x->parent->right;
                }
                w->color = x->parent->color;
                x->parent->color = BLACK;
                w->right->color = BLACK;
                leftRotate(T,x->parent);
                x = T->root;
            }
        } else {
            RbTreeNode *w = x->parent->left;
            if (w->color == RED) {
                w->color = BLACK;
                x->parent->color = RED;
                rightRotate(T,x->parent);
                w = x->parent->left;
            }
            if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
                w->color = RED;
                x = x->parent;
            } else {
                if (w->left->color == BLACK) {
                    w->right->color = BLACK;
                    w->color = RED;
                    leftRotate(T,w);
                    w = x->parent->left;
                }

                w->color = x->parent->color;
                x->parent->color = BLACK;
                w->left->color = BLACK;
                rightRotate(T,x->parent);

                x = T->root;
            }
        }
    }
    x->color = BLACK;
}

// 删除节点
RbTreeNode* rbTreeDelete(RbTree *T, RbTreeNode *z) {
    // z是被覆盖的节点 y是删除节点 x是轴心节点负责旋转
    RbTreeNode *y = T->nil;
    RbTreeNode *x = T->nil;

    // 此时如果没有子树或只有一颗子树 那么就是要被删除的节点
    if ((z->left == T->nil) || (z->right == T->nil)) {
        y = z;
    } else {
        // 寻找删除节点 也就是覆盖节点的右子树的最左节点
        y = rbTree_successor(T,z);
    }

    // 找轴心节点 一般是被删除节点的左子节点
    if (y->left != T->nil) {
        x = y->left;
    } else if (y->right != T->nil) {
        x = y->right;
    }

    x->parent = y->parent;
    if (y->parent == T->nil) {
        // 如果y是根节点 那么x就成为新的根节点
        T->root = x;
    } else if (y == y->parent->left) {
        y->parent->left = x;
    } else {
        y->parent->right = x;
    }

    // 覆盖节点
    if (y != z) {
        z->key = y->key;
        z->value = y->value;
    }

    // 如果删除节点是黑色节点则需要调整
    if (y->color == BLACK) {
        rbTree_delete_fixup(T,x);
    }

    return y;
}

时间复杂度

红黑树的时间复杂度：

• 查询元素O(logN)
• 插入元素：最多只需要两次旋转，最少一次旋转就可以完成，甚至有时候不需要调整
• 删除元素：最多也只需要三次旋转，最少一次旋转就可以完成，甚至有时候不需要调整

AVL树的时间复杂度：

• 查询元素O(logn)
• 插入元素：最多两次旋转就可以保存平衡
• 删除元素：AVL树需要维护被删除节点到根节点路径上所有节点的平衡性，需要大量的旋转

就插入节点导致树失衡的情况，AVL和RB-Tree都是最多两次树旋转来实现复衡，旋转的量级是O(1)

删除节点导致失衡，AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而RB-Tree最多只需要旋转3次实现复衡，只需O(1)，所以说RB-Tree删除节点的rebalance的效率更高，开销更小！

但是红黑树是通过改变节点颜色来避免旋转，具体开销还是要看改变颜色开销小还是改变指针开销小