算法基础课学习笔记：（二）前缀和与差分

算法基础课学习笔记：（二）前缀和与差分

写文章真的好花时间hh，虽然没人看，俺就当记录了

算法介绍

1.前缀和

       我们先引入一个经典问题，给定一串巨长的数据，再给出数十万组询问，每次询问某个区间内数字的总和是多少。来看一组数据：
                                                        
       此时我们假定两次询问：第一次询问区间[1,4]之间的数字和，第二次询问区间[2,5]之间的数字和。
       接下来我们展开讨论，如果利用最朴素的暴力思想，那就是定位到区间[a,b]的左端点，以第一次询问举例，也就是定位到下标为1的元素处。再将元素不断相加到下标4的元素处，得到数字和为64。对第二次询问也可以做同样的操作，得到数字和为60。
       但不妨来考虑一下这种做法的时间复杂度，我们假定每次询问区间的平均长度为$n$，那我们的时间复杂度就是$o(nm)$，$m$为询问次数。这样的时间复杂度在小规模数据下的表现是良好的，但我们这个问题的前提是：一串巨长的数据以及数十万次询问。假设我们的$n$为1000，那运行时间就达到了数亿级别，远远超过了普通计算机一秒内能处理的运算量。
       但是！在面试题和算法题里通常给出的时间限制都是1s！问题就来了，我们怎样才能在1s的时间限制内处理这么多次询问以及巨大的数据量呢？
       这里就要引入前缀和的概念。
       
       前缀和的作用是：在数据量规模极大的情况下，能够以$o(1)$的时间复杂度，处理一次询问的区间数字和。
       

1.1暴力算法优化

       我们先来观察一下举例的两次询问，在区间[1,4]和区间[2,5]的数字和统计中，有没有重复计算可以省去。可以很轻松地发现，区间[2,4]上的数字和在两次询问中都被用到了，这就造成了重复计算。优化算法就是要减少重复计算。
       如何才能减少重复计算呢，最好的办法就是将这些可能会用到的重复计算量提取处理好，在后续操作过程中直接调用处理好的数据。
       我们再来看这组数据
                                                        
       要计算区间[1,4]之间的数字和，我们是否可以将A[5]之前的数字和计算出来，再减去A[1]之前的数字和，得到区间[1,4]之间的数字和。答案是显然的。
       同理，区间[2,5]之间的数字和，也可以用A[6]之前的数字和减去A[2]之前的数字和。
       
       此时，我们就发现了一个重要性质，求区间[a,b]之间的数字和，可以用区间[1,b+1]的数字和减去区间[1,a]之间的数字和。
       我们记下标$n$之前所有元素的数字和为$sum[n]$，公式则化简为：
       
                                                        $区间[a,b]的数字和=sum[b+1]-sum[a]$
       
       显然，相减操作的时间复杂度为$o(1)$，所以我们只要提前得到所有的$sum[n]$的值，就可以在短短的时间内，得到区间和，减少了重复操作。
       
       这种预先处理好$sum$数组值的操作就被称为前缀和，数组里保存的是从$1$个元素开始到第$n$个元素的数字和。
       

1.2前缀和代码模板及效率对比

       这里给出前缀和的模板代码：

int main(){
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+A[i];  //处理前缀和数组sum

    while(m--){                       //进行多次询问
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",s[r]-s[l-1]);
    }

    return 0;
}

       我们来比较一下朴素暴力算法与前缀和算法在处理这类问题下的效率：
                                          
                                                                             前缀和算法时间耗时
       
       暴力直接TLE了hh，数据范围还仅仅是在$10^6$内。
                     

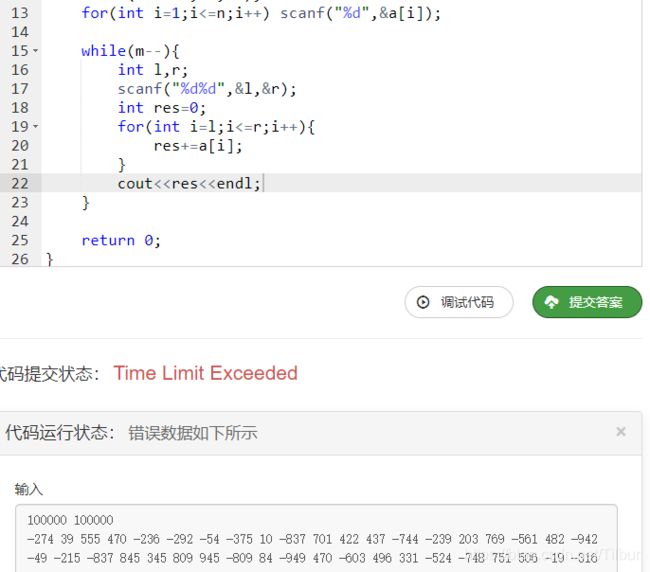
       由此可见，在采用前缀和算法后能对程序运行效率优化。
       本文仅是对一维前缀和做了讨论，读者可以自行思考后尝试二维前缀和如何实现。
       

2.差分

       我们再提出一个经典问题，给定一串巨长的数据，再给出数十万组操作，每次操作让数组内某段区间的所有元素都加上$c$，最后输出整段数据。再看这组数据：
                                                        
       如果让区间[1,4]和区间[2,5]内所有元素都加上$3$，最后输出整段数据。
       显然暴力做法也是扫描[1,4]和[2,5]里的每一个元素，逐个加上$3$后输出数组。
       我们来讨论一下这样处理的时间复杂度，我们假定每次操作区间的平均长度为$n$，那我们的时间复杂度就是$o(nm)$，$m$为操作次数。好吧，显而易见，在数十万组操作的情况下，绝对会超时。
       
       那我们来思考是否有和前缀和一样的思想，来让每次区间元素相加的时间复杂度降到$o(1)$呢？直接了当地告诉你，把这段数组当作是处理好的前缀和就好啦。
       
       我们将该数组作为前缀和$sum$数组，求其原数组为$B$数组。
       
       来看一下$B$数组的计算公式：
                                                                      $B[n]=A[n]-A[n-1]$
       
       这样得到$B$数组后，我们就可以直接将在区间[a,b]内重复添加某数$c$的操作化简为：
                                                        $B[a]=B[a]+c,B[b+1]=B[b+1]-c$
       
       只要这样操作，我们就能将重复添加的操作的时间复杂度降下来。
       
       但问题是为什么能这样处理呢？
       
       注意到！现在的$B$数组是把$A$数组当作前缀和后求出的原数组，相当于前缀和的逆运算。我们来复现一下求前缀和的操作：
                                                               $A[2]=A[1]+B[2]$
                                                               $A[3]=A[2]+B[3]$
                                                                             $...$
                                                             $A[n]=A[n-1]+B[n]$
       当$B[a]$加上了数$c$后，从$A[a]$开始的每个数都会自动加上一个$c$，因为这个常数被包含在$B[a]$里后被求前缀和的操作重复添加了。
       当操作进行到$A[b]$时，我们让$B[b+1]=B[b+1]-c$这样就会让$A[b]$之后的元素都少加上一个$c$，与前面的操作相抵了。
       
       这种算法思想就叫做差分，我们可以在$o(1)$的时间复杂度内操作极长区间的数据加减一个常数。
       

2.2差分代码模板

       这里给出差分的代码模板：

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) b[i]=a[i]-a[i-1];  //求差分数组B
	
	while(m--){
		int l,r,c;
		scanf("%d%d%d",&l,&r,&c);
		b[l]+=c;
		b[r+1]-=c;
	}
	
	for(int i=1;i<=n;i++) a[i]=a[i-1]+b[i];   //再求回原数组
	for(int i=1;i<=n;i++) printf("%d ",a[i]);
	
	return 0;
}

总结

       差分和前缀和是常考的基础算法，如果看不懂算法思想，一定是我太菜了hh，讲不清楚。可以去看看y总的视频，理的比较清楚。
       最后再来说一遍两个算法的应用范围：
       前缀和：用来求大规模数据及大批量询问下的某段区间元素和
       差分：用来快速地在大规模地操作数据加减常数时，减少重复操作的次数，提高效率