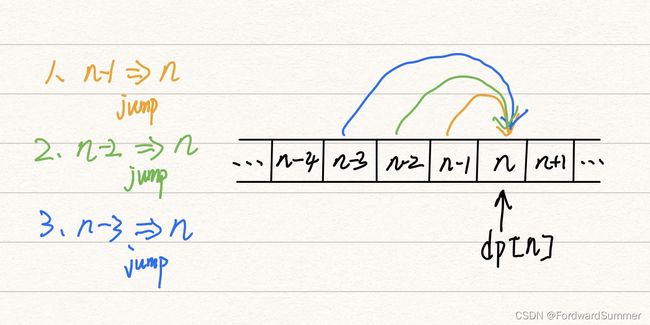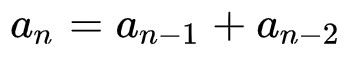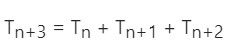Java-算法-动态规划
前置条件
动态规划最重要的是转移方程,而转移方程需要递归和记忆化搜索产生的表,因此直接贴出转移方程是没什么用的,不探究如何从递归到记忆化搜索再到转移方程,还是很难想到怎么去得到转移方程。下面我们将从例子中探寻如何三步走。
例一.
按摩师
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
输入: [1,2,3,1] 输出: 4 解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。 输入: [2,7,9,3,1] 输出: 12 解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。
(1)递归
class Solution {
public int massage(int[] nums) {
return process(nums,0);
}
public int process(int[] nums,int i){
if(i >= nums.length){
return 0;
}
return Math.max(process(nums,i+1),nums[i] + process(nums,i+2));
}
}(2)记忆化搜索
class Solution {
public int massage(int[] nums) {
int[] dp = new int [nums.length];
Arrays.fill(dp,-1);
return process(nums,0,dp);
}
public int process(int[] nums,int i,int[] dp){
if(i >= nums.length){
return 0;
}
if(dp[i] != -1){
return dp[i];
}
int notchocie = process(nums,i+1,dp);
int chocie = nums[i] + process(nums,i+2,dp);
dp[i] = Math.max(notchocie,chocie);
return dp[i];
}
}(3)动态规划
class Solution {
public int massage(int[] nums) {
if(nums == null || nums.length== 0) return 0;
if(nums.length == 1) return nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
int ans = dp[1];
for(int i = 2; i < nums.length; i++){
dp[i] = Math.max(dp[i-1],nums[i]+dp[i-2]);
ans = Math.max(dp[i],ans);
}
return ans;
}
}例二.
三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
(1)递归
二话不说先递归,递归停止的条件为正好跳到n的位置和跳过n的位置
1.跳到n的位置说明有一种可能性。
2.跳过n的位置说明此时这种情况会跳出n的位置,这种情况不考虑。
class Solution {
public int waysToStep(int n) {
return process(n,0);
}
public int process(int n, int cur){
if( cur == n){
return 1;
}
if( cur > n){
return 0;
}
return process(n,cur+1) + process(n,cur+2) + process(n,cur+3);
}
}
(2)记忆化搜索
class Solution {
public int waysToStep(int n) {
int[] dp = new int[n+3];
Arrays.fill(dp,-1);
return process(n,0,dp);
}
public int process(int n, int cur,int[] dp){
if(dp[cur] != -1) return dp[cur];
if( cur > n){
dp[cur] = 0;
return 0;
}
if( cur == n){
dp[cur] = 1;
return 1;
}
return process(n,cur+1,dp) + process(n,cur+2,dp) + process(n,cur+3,dp);
}
}
(3)动态规划
我们来到第n个阶梯,向前溯源,可以发现我们可以从三个位置跳到n的位置,分别是
1.从n-1跳一格
2.从n-2跳二格
3.从n-3跳三格
假设此时过去三个位置我们都知道在那个位置上有多少种情况,
只要把三个情况都加起来就可以了
class Solution {
public int waysToStep(int n) {
long[] dp = new long[n+3];
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i = 4; i <= n; i++){
dp[i] = (dp[i-1] + dp[i-2] + dp[i-3])%1000000007;
}
return (int)dp[n];
}
}
斐波那契数列为
而此题是斐波那契数的变换版本
可以参考 leetcode509. 斐波那契数和leetcode1137. 第 N 个泰波那契数
而此题的状态转移方程为
class Solution {
public int waysToStep(int n) {
if(n <= 2) return n;
long a = 1;
long b = 1;
long c = 2;
long t = 0;
for(int i = 3; i <= n; i++){
t = (c + b + a)%1000000007;
a = b;
b = c;
c = t;
}
return (int)t;
}
}
例三.
leetcode石子游戏
Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子,排成一行;每堆都有 正 整数颗石子,数目为 piles[i] 。游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ,所以没有平局。
Alice 和 Bob 轮流进行,Alice 先开始 。 每回合,玩家从行的 开始 或 结束 处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中 石子最多 的玩家 获胜 。
假设 Alice 和 Bob 都发挥出最佳水平,当 Alice 赢得比赛时返回 true ,当 Bob 赢得比赛时返回 false 。
输入:piles = [5,3,4,5]
输出:true
解释:
Alice 先开始,只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗,这一行就变成了 [3,4,5] 。
如果 Bob 拿走前 3 颗,那么剩下的是 [4,5],Alice 拿走后 5 颗赢得 10 分。
如果 Bob 拿走后 5 颗,那么剩下的是 [3,4],Alice 拿走后 4 颗赢得 9 分。
这表明,取前 5 颗石子对 Alice 来说是一个胜利的举动,所以返回 true 。
(1)递归,超出时间限制
class Solution {
public boolean stoneGame(int[] piles) {
return f(piles,0,piles.length-1) > s(piles,0,piles.length-1);
}
public int f(int[] arr, int L, int R){
if(L == R){
return arr[L];
}
return Math.max(
arr[L] + s(arr,L+1,R),
arr[R] + s(arr,L,R-1)
);
}
public int s(int[] arr, int L, int R){
if(L == R){
return 0;
}
return Math.min(
f(arr,L+1,R),
f(arr,L,R-1)
);
}
}(2)记忆化搜索,29ms
class Solution {
int[][] dpmax;
int[][] dpmin;
public boolean stoneGame(int[] piles) {
dpmax = new int[piles.length][piles.length];
dpmin = new int[piles.length][piles.length];
for(int[] arr : dpmax){
Arrays.fill(arr,-1);
}
for(int[] arr : dpmin){
Arrays.fill(arr,-1);
}
return first(piles,0,piles.length-1) > second(piles,0,piles.length-1);
}
public int first(int[] arr, int L, int R){
if(dpmax[L][R] != -1){
return dpmax[L][R];
}
if(L == R){
dpmax[L][R] = arr[L];
return arr[L];
}
int max = Math.max(
arr[L] + second(arr,L+1,R),
arr[R] + second(arr,L,R-1)
);
dpmax[L][R] = max;
return max;
}
public int second(int[] arr, int L, int R){
if(dpmin[L][R] != -1){
return dpmin[L][R];
}
if(L == R){
dpmin[L][R] = 0;
return 0;
}
int min = Math.min(
first(arr,L+1,R),
first(arr,L,R-1)
);
dpmin[L][R] = min;
return min;
}
}(3)动态规划,5ms
class Solution {
public boolean stoneGame(int[] piles) {
int[][] dpmax = new int[piles.length][piles.length];
int[][] dpmin = new int[piles.length][piles.length];
for(int[] arr : dpmax){
Arrays.fill(arr,0);
}
for(int[] arr : dpmin){
Arrays.fill(arr,0);
}
int L = 0;
int R =piles.length-1;
int max = 0;
int min = 0;
while(L < R ){
max += Math.max(dpmin[L+1][R]+piles[L],dpmin[L][R-1]+piles[R]);
dpmax[L][R] = max;
min += Math.min(piles[L]+dpmax[L+1][R],piles[R]+dpmax[L][R-1]);
dpmin[L][R] = min;
L++;
R--;
}
return max > min;
}
}public static int win2(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int[][] f = new int[arr.length][arr.length];
int[][] s = new int[arr.length][arr.length];
for (int j = 0; j < arr.length; j++) {
f[j][j] = arr[j];
for (int i = j - 1; i >= 0; i--) {
f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
}
}
return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
}状态转移表格