面向对象编程(基础)7:再谈方法(重载)
目录
7.1 方法的重载(overload)
7.1.1 概念及特点
7.1.2 示例
举例1:
举例2:
举例3:方法的重载和返回值类型无关
7.1.3 练习
**练习1:**
练习2:编写程序,定义三个重载方法并调用。
练习3:
7.2 可变个数的形参
格式:
举例:
特点:
案例分析:
案例1:n个字符串进行拼接,每一个字符串之间使用某字符进行分割,如果没有传入字符串,那么返回空字符串""
案例2:求n个整数的和
案例3:如下的方法彼此构成重载
7.3 方法的参数传递机制
7.3.1 形参和实参
7.3.2 参数传递机制:值传递
7.3.3 举例
1、形参是基本数据类型
2、形参是引用数据类型
7.3.4 练习
练习1:判断如下程序输出的结果
练习2:如下操作是否可以实现数组排序
练习3:通过内存结构图,写出如下程序的输出结果
练习4:貌似是考查方法的参数传递
练习5:将对象作为参数传递给方法
7.4 递归(recursion)方法
举例1:
举例2
递归方法调用:方法自己调用自己的现象就称为递归。
直接递归:方法自身调用自己。
间接递归:可以理解为A()方法调用B()方法,B()方法调用C()方法,C()方法调用A()方法。
举例:
举例1:计算1 ~ n的和
举例2:递归方法计算n!
举例3:已知有一个数列:f(0) = 1,f(1) = 4,f(n+2)=2*f(n+1) + f(n),其中n是大于0的整数,求f(10)的值。
举例4:已知一个数列:f(20) = 1,f(21) = 4,f(n+2) = 2*f(n+1)+f(n),其中n是大于0的整数,求f(10)的值。
举例5:计算斐波那契数列(Fibonacci)的第n个值,斐波那契数列满足如下规律,
举例6:面试题
最后说两句:
7.1 方法的重载(overload)
7.1.1 概念及特点
- 方法重载:在同一个类中,允许存在一个以上的同名方法,只要它们的参数列表不同即可。
- 参数列表不同,意味着参数个数或参数类型的不同
- 重载的特点:与修饰符、返回值类型无关,只看参数列表,且参数列表必须不同。(参数个数或参数类型)。调用时,根据方法参数列表的不同来区别。
- 重载方法调用:JVM通过方法的参数列表,调用匹配的方法。
- 先找个数、类型最匹配的
- 再找个数和类型可以兼容的,如果同时多个方法可以兼容将会报错
7.1.2 示例
举例1:
//System.out.println()方法就是典型的重载方法,其内部的声明形式如下:
public class PrintStream {
public void println(byte x)
public void println(short x)
public void println(int x)
public void println(long x)
public void println(float x)
public void println(double x)
public void println(char x)
public void println(double x)
public void println()
}
public class HelloWorld{
public static void main(String[] args) {
System.out.println(3);
System.out.println(1.2f);
System.out.println("hello!");
}
}
举例2:
//返回两个整数的和
public int add(int x,int y){
return x+y;
}
//返回三个整数的和
public int add(int x,int y,int z){
return x+y+z;
}
//返回两个小数的和
public double add(double x,double y){
return x+y;
}
举例3:方法的重载和返回值类型无关
public class MathTools {
//以下方法不是重载,会报错
public int getOneToHundred(){
return (int)(Math.random()*100);
}
public double getOneToHundred(){
return Math.random()*100;
}
}
7.1.3 练习
**练习1:**
判 断与void show(int a,char b,double c){}构成重载的有:
a)void show(int x,char y,double z){} // no
b)int show(int a,double c,char b){} // yes
c) void show(int a,double c,char b){} // yes
d) boolean show(int c,char b){} // yes
e) void show(double c){} // yes
f) double show(int x,char y,double z){} // no
g) void shows(){double c} // no
练习2:编写程序,定义三个重载方法并调用。
-
方法名为mOL。
-
三个方法分别接收一个int参数、两个int参数、一个字符串参数。分别执行平方运算并输出结果,相乘并输出结果,输出字符串信息。
-
在主类的main ()方法中分别用参数区别调用三个方法。
练习3:
定义三个重载方法max(),第一个方法求两个int值中的最大值,第二个方法求两个double值中的最大值,第三个方法求三个double值中的最大值,并分别调用三个方法。
7.2 可变个数的形参
在**JDK 5.0 中提供了Varargs(variable number of arguments)**机制。即当定义一个方法时,形参的类型可以确定,但是形参的个数不确定,那么可以考虑使用可变个数的形参。
格式:
方法名(参数的类型名 ...参数名)
举例:
//JDK 5.0以前:采用数组形参来定义方法,传入多个同一类型变量
public static void test(int a ,String[] books);
//JDK5.0:采用可变个数形参来定义方法,传入多个同一类型变量
public static void test(int a ,String...books);
特点:
-
可变参数:方法参数部分指定类型的参数个数是可变多个:0个,1个或多个
-
可变个数形参的方法与同名的方法之间,彼此构成重载
-
可变参数方法的使用与方法参数部分使用数组是一致的,二者不能同时声明,否则报错。
-
方法的参数部分有可变形参,需要放在形参声明的最后
-
在一个方法的形参中,最多只能声明一个可变个数的形参
案例分析:
案例1:n个字符串进行拼接,每一个字符串之间使用某字符进行分割,如果没有传入字符串,那么返回空字符串""
public class StringTools {
String concat(char seperator, String... args){
String str = "";
for (int i = 0; i < args.length; i++) {
if(i==0){
str += args[i];
}else{
str += seperator + args[i];
}
}
return str;
}
}
package com.atguigu.test05.param;
public class StringToolsTest {
public static void main(String[] args) {
StringTools tools = new StringTools();
System.out.println(tools.concat('-'));
System.out.println(tools.concat('-',"hello"));
System.out.println(tools.concat('-',"hello","world"));
System.out.println(tools.concat('-',"hello","world","java"));
}
}
案例2:求n个整数的和
public class NumberTools {
public int total(int[] nums){
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
return sum;
}
public int sum(int... nums){
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
return sum;
}
}
public class TestVarParam {
public static void main(String[] args) {
NumberTools tools = new NumberTools();
System.out.println(tools.sum());//0个实参
System.out.println(tools.sum(5));//1个实参
System.out.println(tools.sum(5,6,2,4));//4个实参
System.out.println(tools.sum(new int[]{5,6,2,4}));//传入数组实参
System.out.println("------------------------------------");
System.out.println(tools.total(new int[]{}));//0个元素的数组
System.out.println(tools.total(new int[]{5}));//1个元素的数组
System.out.println(tools.total(new int[]{5,6,2,4}));//传入数组实参
}
}
案例3:如下的方法彼此构成重载
public class MathTools {
//求两个整数的最大值
public int max(int a,int b){
return a>b?a:b;
}
//求两个小数的最大值
public double max(double a, double b){
return a>b?a:b;
}
//求三个整数的最大值
public int max(int a, int b, int c){
return max(max(a,b),c);
}
//求n个整数的最大值
public int max(int... nums){
int max = nums[0];//如果没有传入整数,或者传入null,这句代码会报异常
for (int i = 1; i < nums.length; i++) {
if(nums[i] > max){
max = nums[i];
}
}
return max;
}
/* //求n整数的最大值
public int max(int[] nums){ //编译就报错,与(int... nums)无法区分
int max = nums[0];//如果没有传入整数,或者传入null,这句代码会报异常
for (int i = 1; i < nums.length; i++) {
if(nums[i] > max){
max = nums[i];
}
}
return max;
}*/
/* //求n整数的最大值
public int max(int first, int... nums){ //当前类不报错,但是调用时会引起多个方法同时匹配
int max = first;
for (int i = 0; i < nums.length; i++) {
if(nums[i] > max){
max = nums[i];
}
}
return max;
}*/
}
7.3 方法的参数传递机制
7.3.1 形参和实参
- 形参(formal parameter):在定义方法时,方法名后面括号()中声明的变量称为形式参数,简称形参。
- 实参(actual parameter):在调用方法时,方法名后面括号()中的使用的值/变量/表达式称为实际参数,简称实参。
7.3.2 参数传递机制:值传递
Java里方法的参数传递方式只有一种:值传递。 即将实际参数值的副本(复制品)传入方法内,而参数本身不受影响。
-
形参是基本数据类型:将实参基本数据类型变量的“数据值”传递给形参
-
形参是引用数据类型:将实参引用数据类型变量的“地址值”传递给形参
7.3.3 举例
1、形参是基本数据类型
案例:编写方法,交换两个整型变量的值
public class Test {
public static void main(String[] args) {
int m = 10;
int n = 20;
System.out.println("m = " + m + ", n = " + n);
//交换m和n的值
// int temp = m;
// m = n;
// n = temp;
ValueTransferTest1 test = new ValueTransferTest1();
test.swap(m, n);
System.out.println("m = " + m + ", n = " + n);
}
public void swap(int m,int n){
int temp = m;
m = n;
n = temp;
}
}
内存解析:
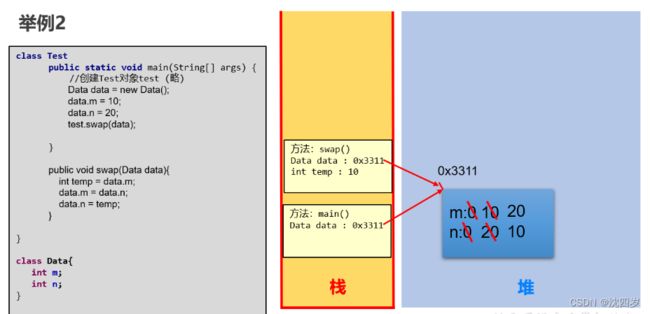
2、形参是引用数据类型
public class Test {
public static void main(String[] args) {
Data d1 = new Data();
d1.m = 10;
d1.n = 20;
System.out.println("m = " + d1.m + ", n = " + d1.n);
//实现 换序
ValueTransferTest2 test = new ValueTransferTest2();
test.swap(d1);
System.out.println("m = " + d1.m + ", n = " + d1.n);
}
public void swap(Data data){
int temp = data.m;
data.m = data.n;
data.n = temp;
}
}
class Data{
int m;
int n;
}
7.3.4 练习
练习1:判断如下程序输出的结果
public class AssignNewObject {
public void swap(MyData my){
my = new MyData(); //考虑堆空间此新创建的对象,和main中的data对象是否有关
int temp = my.x;
my.x = my.y;
my.y = temp;
}
public static void main(String[] args) {
AssignNewObject tools = new AssignNewObject();
MyData data = new MyData();
data.x = 1;
data.y = 2;
System.out.println("交换之前:x = " + data.x +",y = " + data.y);//
tools.swap(data);//调用完之后,x与y的值交换?
System.out.println("交换之后:x = " + data.x +",y = " + data.y);//
}
}
class MyData{
int x ;
int y;
}
练习2:如下操作是否可以实现数组排序
public class ArrayTypeParam {
//冒泡排序,实现数组从小到大排序
public void sort(int[] arr){
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if(arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
//打印数组的元素
public void print(int[] arr){
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
public static void main(String[] args) {
ArrayTypeParam tools = new ArrayTypeParam();
int[] nums = {4,3,1,6,7};
System.out.println("排序之前:");
tools.print(nums);
tools.sort(nums);//对nums数组进行排序
System.out.println("排序之后:");
tools.print(nums);//输出nums数组的元素
}
}
练习3:通过内存结构图,写出如下程序的输出结果
//栈:每个方法在调用时,都会有以栈帧的方法压入栈中。栈帧中保存了当前方法中声明的变量:方法内声明的,形参
//堆:存放new出来的"东西":对象(成员变量在对象中)、数组实体(数组元素)。
//注意:变量前如果声明有类型,那么这就是一个新的刚要定义的变量。如果变量前没有声明类型,那就说明此变量在之前已经声明过。
public class TransferTest3 {
public static void main(String args[]) {
TransferTest3 test = new TransferTest3();
test.first();
}
public void first() {
int i = 5;
Value v = new Value();
v.i = 25;
second(v, i);
System.out.println(v.i);
}
public void second(Value v, int i) {
i = 0;
v.i = 20;
Value val = new Value();
v = val;
System.out.println(v.i + " " + i);
}
}
class Value {
int i = 15;
}
内存解析:
练习4:貌似是考查方法的参数传递
//法一:
public static void method(int a, int b) {
// 在不改变原本题目的前提下,如何写这个函数才能在main函数中输出a=100,b=200?
a = a * 10;
b = b * 20;
System.out.println(a);
System.out.println(b);
System.exit(0);
}
//法二:
public static void method(int a, int b) {
PrintStream ps = new PrintStream(System.out) {
@Override
public void println(String x) {
if ("a=10".equals(x)) {
x = "a=100";
} else if ("b=10".equals(x)) {
x = "b=200";
}
super.println(x);
}
};
System.setOut(ps);
}
练习5:将对象作为参数传递给方法
(1)定义一个Circle类,包含一个double型的radius属性代表圆的半径,一个findArea()方法返回圆的面积。
(2)定义一个类PassObject,在类中定义一个方法printAreas(),该方法的定义如下:public void printAreas(Circle c, int time),在printAreas方法中打印输出1到time之间的每个整数半径值,以及对应的面积。例如,times为5,则输出半径1,2,3,4,5,以及对应的圆面积。
(3)在main方法中调用printAreas()方法,调用完毕后输出当前半径值。程序运行结果如图所示。
7.4 递归(recursion)方法
举例1:
举例2
从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,讲的啥?
从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,讲的啥?
从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,讲的啥?
从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,讲的啥?...
...
老和尚没了,庙塌了,小和尚还俗结婚了。
递归方法调用:方法自己调用自己的现象就称为递归。
**递归的分类:**直接递归、间接递归。
-
直接递归:方法自身调用自己。
public void methodA(){
methodA();
}
间接递归:可以理解为A()方法调用B()方法,B()方法调用C()方法,C()方法调用A()方法。
public static void A(){
B();
}
public static void B(){
C();
}
public static void C(){
A();
}
说明:
- 递归方法包含了一种
隐式的循环。 - 递归方法会
重复执行某段代码,但这种重复执行无须循环控制。 - 递归一定要向
已知方向递归,否则这种递归就变成了无穷递归,停不下来,类似于死循环。最终发生栈内存溢出。
举例:
举例1:计算1 ~ n的和
public class RecursionDemo {
public static void main(String[] args) {
RecursionDemo demo = new RecursionDemo();
//计算1~num的和,使用递归完成
int num = 5;
// 调用求和的方法
int sum = demo.getSum(num);
// 输出结果
System.out.println(sum);
}
/*
通过递归算法实现.
参数列表:int
返回值类型: int
*/
public int getSum(int num) {
/*
num为1时,方法返回1,
相当于是方法的出口,num总有是1的情况
*/
if(num == 1){
return 1;
}
/*
num不为1时,方法返回 num +(num-1)的累和
递归调用getSum方法
*/
return num + getSum(num-1);
}
}
代码执行图解:
举例2:递归方法计算n!
public int multiply(int num){
if(num == 1){
return 1;
}else{
return num * multiply(num - 1);
}
}
举例3:已知有一个数列:f(0) = 1,f(1) = 4,f(n+2)=2*f(n+1) + f(n),其中n是大于0的整数,求f(10)的值。
public int f(int num){
if(num == 0){
return 1;
}else if(num == 1){
return 4;
}else{
return 2 * f(num - 1) + f(num - 2);
}
}
举例4:已知一个数列:f(20) = 1,f(21) = 4,f(n+2) = 2*f(n+1)+f(n),其中n是大于0的整数,求f(10)的值。
public int func(int num){
if(num == 20){
return 1;
}else if(num == 21){
return 4;
}else{
return func(num + 2) - 2 * func(num + 1);
}
}
举例5:计算斐波那契数列(Fibonacci)的第n个值,斐波那契数列满足如下规律,
1,1,2,3,5,8,13,21,34,55,....
即从第三个数开始,一个数等于前两个数之和。假设f(n)代表斐波那契数列的第n个值,那么f(n)满足:
f(n) = f(n-2) + f(n-1);
//使用递归的写法
int f(int n) {//计算斐波那契数列第n个值是多少
if (n < 1) {//负数是返回特殊值1,表示不计算负数情况
return 1;
}
if (n == 1 || n == 2) {
return 1;
}
return f(n - 2) + f(n - 1);
}
//不用递归
int fValue(int n) {//计算斐波那契数列第n个值是多少
if (n < 1) {//负数是返回特殊值1,表示不计算负数情况
return 1;
}
if (n == 1 || n == 2) {
return 1;
}
//从第三个数开始, 等于 前两个整数相加
int beforeBefore = 1; //相当于n=1时的值
int before = 1;//相当于n=2时的值
int current = beforeBefore + before; //相当于n=3的值
//再完后
for (int i = 4; i <= n; i++) {
beforeBefore = before;
before = current;
current = beforeBefore + before;
/*
假设i=4
beforeBefore = before; //相当于n=2时的值
before = current; //相当于n=3的值
current = beforeBefore + before; //相当于n = 4的值
假设i=5
beforeBefore = before; //相当于n=3的值
before = current; //相当于n = 4的值
current = beforeBefore + before; //相当于n = 5的值
....
*/
}
return current;
}
举例6:面试题
宋老师,我今天去百度面试,遇到一个一个双重递归调用的问题,我琢磨了一下,完全不知道为什么。打断点了,也还是没看懂为什么程序会那样走。您有空可以看一下,求指教
private int count = 0;
public int recursion(int k) {
count++;
System.out.println("count1:" + count + " k:" + k);
if (k <= 0) {
return 0;
}
return recursion(k - 1) + recursion(k - 2);//287
//return recursion(k - 1);//11
//return recursion(k - 1) + recursion(k - 1);//2047
}
剖析:
最后说两句:
-
递归调用会占用大量的系统堆栈,内存耗用多,在递归调用层次多时速度要比循环
慢的多,所以在使用递归时要慎重。 -
在要求高性能的情况下尽量避免使用递归,递归调用既花时间又
耗内存。考虑使用循环迭代