Josh 的学习笔记之数字通信（Part 5——通信链路分析）

1. 系统工程中的系统链路预算

  通信链路（link）属于系统的哪一部分？链路不仅指发射机与接收机之间的信道或者区域，还包括整个通信路径：从信源开始，通过所有的编码和调制过程，经由发射机和信道，直到包含所有信号处理功能的接收机，最后结束于信宿。

  下面介绍链路分析的定义，并解释链路分析在通信系统设计中的作用。进行链路分析并得出结果的过程称为链路预算（link budget），整个过程包括对接收端获得的有用信号功率、干扰噪声功率的计算和表格化。链路预算权衡了增益和损耗，概括了发送接收资源、噪声源和信号衰减的详细分配比例，及其对整个链路过程的影响。链路预算是一种评价通信系统差错性能的评估（estimation）技术。在《Part 3——基带信号解调与检测》、《Part 4——带通调制和解调》中已经介绍， 差错概率与 $E_b/N_0$ 的关系曲线具有“像瀑布一样”的形状，如图 3.5 所示。对于高斯噪声信道的各种调制方式而言，其 $E_b/N_0$ 与差错概率相关联。一旦选定调制方式， 给定的差错概率就对应着曲线图上的某一点。换言之，要求的差错性能规定了满足性能要求的接收机所要达到的 $E_b/N_0$ 值。链路分析的主要目的是确定图 3.5 的实际（actual）系统工作点、并验证该点的差错概率小于或者等于系统的要求。在通信系统设计时使用的许多说明、分析和制表中，链路预算是一个重要的基本工具，它为系统工程师提供对系统的整体了解。

  通过链路预算，可以知道整个系统的设计和性能。例如，链路余量可以说明系统能充裕地、还是刚好或根本不能满足需求。链路分析可以反映系统是否存在硬件限制，以及是否能在链路的其他部分弥补该限制。链路预算经常作为分析系统权衡、配置变化以及系统细微变化和相关性的参考依据，并且，若将其与其他建模技术结合，将有助于预测设备的重量和大小、主要功率要求、技术风险以及系统成本。链路预算对系统工程师来说至关重要，它代表了系统性能优化的“底线”。

---

2. 信道

  信道（channel）是连接发射机和接收机的传播媒介或电磁波通道。通信信道一般包括导线、同轴电缆、光纤线缆，若是射频（RF）链路，则包括波导、大气层或真空。

• 对大多数地面通信链路来说，信道空间由大气层构成，部分与地球表面相连。
• 对于卫星链路而言，信道则主要由真空构成。

尽管在 100 km 的高度上仍存在一定的大气影响，但是通常大气层容积定义在高度为 20 km 的范围内。因此，在同步高度（35 800 km）路径中只有很少一部分（0.05%）才是大气层。本文介绍的链路分析主要针对这样的卫星通信链路，在 Part 15 中对链路预算的分析将扩展到地面无线链路。

2.1 自由空间的概念

  自由空间（free space）是指在射频传播中没有任何吸收、反射、辐射或衍射等干扰的信道。且须满足以下条件：

• 若信道中有大气存在，其分布必须是完全均匀的并且满足上述所有要求；
• 同时假定地面是无穷远的，或者地面的反射系数可以忽略不计；
• 且到达接收机的 RF 能量只与到发射机的距离有关（符合光学中平方倒数定律）。

自由空间信道是理想的 RF 传播路径。但是实际上，在大气层和近地点的传播会有吸收、反射、衍射和散射等干扰，这些都会影响信号在自由空间的传输。大气吸收将在后面几节中介绍。反射、衍射和散射对地面通信性能产生的重要影响将在 Part 15 中介绍。

2.2 差错性能的降低

  《Part 3——基带信号解调与检测》已介绍差错性能降低的两个主要原因：

• 首先是信噪比的损失，
• 其次是码间串扰（ISI）导致的信号失真。

《Part 3——基带信号解调与检测》、Part 15 介绍的均衡技术就是为了补偿由于 ISI 引起的性能降低。本文重点关注信号功率、噪声功率的增益和损耗。ISI 不属于链路预算的范围，这是因为信号功率的增加并不总能减少 ISI 引起的性能降低（见《Part 3——基带信号解调与检测》的 3.2 小节）。

  在数字通信中，差错性能依赖于接收端的 $E_b/N_0$，它的定义见为
$$\frac{E_b}{N_0}=\frac{S}{N}\left(\frac{W}{R}\right)$$换言之，$E_b/N_0$ 是归一化的信噪比（$S/N$ 或 SNR）。若没有其他说明，SNR 指平均信号功率与平均噪声功率之比。信号可以是信息信号、基带波形或经调制的载波。SNR 降低的原因有两种：

1. 降低有用信号的功率；
2. 增大噪声功率或者干扰信号功率。

这两种原因分别称为损耗（loss）和噪声（noise，或干扰 interference）。信号的一部分在传播过程中被吸收、转向、分散或反射时就产生了损耗，结果使得部分发射能量不能到达接收端。电磁噪声和干扰的来源很多，比如热噪声、银河系噪声、大气噪声、瞬时切换、互调制噪声以及其他信号源的干扰信号等。使用损耗和噪声这两个术语容易混淆信噪比降低的机理，但它们对 SNR 的影响其实是相同的。

2.3 信号损耗和噪声的来源

  图 5.1 是卫星通信链路的方框图，该图强调了信号损耗和噪声的来源。为了区别信号损耗和噪声源，前者用点状图形表示，后者用线条图形表示，信号损耗和噪声共同作用时用交叉线图形表示。下面列出的是导致 SNR 降低的 21 个主要来源，其序号与图 5.1 的编号一致。

图5.1 包含典型损耗和噪声源的卫星发射机－接收机链路

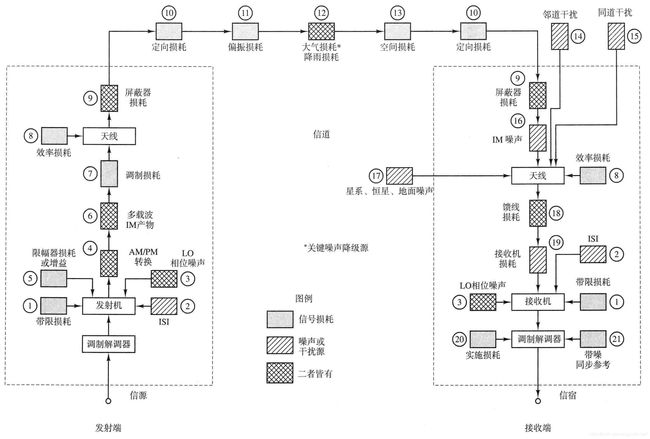
1. 带限损耗：所有的系统在发射机中都使用滤波器，以确保发射能量集中在指定的频带内从而避免对其他信道和用户的干扰，并达到管理部门的要求。这些滤波降低了发射能量，造成了信号的损耗。

2. 码间串扰（ISI）：《Part 3——基带信号解调与检测》已讨论过，系统中所有的滤波（包括发射机、接收机和信道中的滤波）都会产生 ISI。接收脉冲互相叠加，产生的拖尾占据相邻码元的间隔，从而干扰检测过程。即使没有热噪声，不良滤波、系统带宽限制和信道衰落也会产生 ISI，从而导致信噪比降低。

3. 本地振荡器（LO）相位噪声：如果在信号混合中使用 LO，相位变化或抖动将会引入相位噪声。若在接收端的相关器中用该信号作为参考信号，相位跳变会导致检测器性能的降低，从而增加信号损耗。在发射端，相位跳变可能产生信号的带宽扩展，因此需要将扩展的部分滤除，从而造成信号的损耗。

4. AM/PM 转换：在行波管（TWT）等非线性设备中， AM 到 PM 的转换就是一种相位噪声。信号幅度的波动（调幅）产生相位变化，这也给进行相干检测的信号带来了相位噪声。AM 到 PM 的转换还能产生导致信号噪声的额外边带。

5. 限幅器损耗或增强：硬限幅器可以加强两个信号中较大的一个，抑制较小的一个，从而造成信号损耗或者信号增益。

6. 多载波互调制（IM）产物：若几个具有不同载波频率的信号同时通过非线性设备（如 TWT），则会导致不同载波频率间的多重交互作用，产生所有频率的和差组合的信号。这些伪信号（互调或 IM 产物）的能量就是损耗的信号能量。此外，如果这些互调产物出现在信号频带内，则产生了这些信号的附加噪声。

7. 调制损耗：链路预算是计算接收的有用功率（或能量）。只有携带信息的信号功率才是有用的。差错性能是每个传输码元能量的函数。任何用于发射载波信号而不是调制信号的功率都属于调制损耗（但是，载波能量对同步是有用的）。

8. 天线效率：天线是将电信号与电磁信号互相转换的转换器，它也用于将电磁能量汇集于指定的方向。天线口径（面积）越大，指定方向上的信号功率密度也越大。天线效率可以用有效口径和物理口径之比来描述。造成效率降低（信号强度的损耗）的因素有幅度的衰减、口径拥塞、散射、再辐射、溢出、边缘衍射和耗散损失叽由千这些因素的共同作用，导致典型的效率范围是 50%~80%。

9. 天线屏蔽器的损耗和噪声：天线屏蔽器是某些天线上为了防御气候影响而设置的保护层。信号传输路径中的天线屏蔽器会辐射、吸收部分信号能量，从而产生信号损耗。根据物理学基本原理，任何能吸收能址的物体也能辐射能釐（温度在 0 K 以上） 。部分能量落在接收机带宽范围内而导致了注入噪声。

10. 定向损耗：指发射天线或接收天线不正确定向时所产生的损耗。

11. 极化损耗：电磁场极化是指磁力线所指方向的区域，天线的极化则指其辐射域的极化。在发射天线与接收天线之间，任何极化不匹配都会产生信号损耗。

12. 大气损耗和噪声：大气会造成信号损耗，引进有害的噪声。大气的容积在大约 20 km 高度范围之内；在相对较短的信道中，大气会造成主要的损耗和噪声。图 5.2 描述了理论上从指定高度到大气顶端的单向衰减情况，它是在假定地球表面的水蒸气密度为 7.5 g/m³ 时， 针对不同高度计算得到的（海平面为 0 km）。由于氧气（O₂）和水蒸气吸收导致的信号幅度损耗械是载波频率的函数。对水蒸气而言， 衰减的最大值发生在 22 GHz 附近的频段，对氧气而言为 60 GHz 和 120 GHz。大气还给链路带来噪声能量。在天线屏蔽器中，吸收能量的微粒也能辐射能量。氧气和水蒸气微粒在整个 RF 频谱中辐射噪声。落在给定通信系统带宽内的噪声会降低 SNR 。大气造成信号损耗、引进噪声的主要因素是降雨。降雨越稠密，被吸收的信号能量就越多。降雨时由于雨水接触天线束而对系统接收机造成的大气噪声辐射，远远大于晴天时的情况。后面几节中将详细讨论大气噪声。
    
    

图5.2 从指定高度到大气顶端的理论垂直单向衰减，假定表面水蒸气密度为 7.5 g/m³（不含雨云的衰减效果）

13. 空间损耗：电磁场强度的降低，进而引起信号强度（功率密度或流量密度）降低，它是距离的函数。在卫星通信链路中，空间损耗是系统最大的损耗。从某种意义上说，没有会聚到接收天线的所有能量都是损耗。

14. 邻道干扰：这种干扰产生的原因是其他频率信道信号的溢出，而导致的有害信号或者能量的插入。哪一个邻近的信道会落在频域内，由调制的频谱滚降、带宽和主瓣形状决定。

15. 同道干扰：这种干扰指信号带宽内的干扰波形引起的性能降低。造成同道干扰的原因有很多，例如意外发射、缺乏水平和垂直极化识别或天线旁瓣（主天线束周围的低能量束）的辐射溢出等。这种干扰也可能由同频谱的其他授权用户造成。

16. 互调制噪声：第 6 项已介绍，非线性设备中多载波信号的相互作用会产生 IM 产物。该 IM 产物有时也称为能动互调（active intermod），正如第 6 项所述的，它会造成信号能量损耗，或者向链路引入噪声。这里讨论被动互调（passive intermod），这是由于多载波发射信号与发射机输出端的非线性设备相互作用而产生的。这些非线性主要产生于波导耦合连接处、被腐蚀的表面以及弱电的表面。当大的电磁波投射在具有二极管传输函数（势强）的表面时，将产生大量的噪声。如果这些噪声辐射到附近的接收天线，将严重降低接收性能。

17. 银河系或宇宙、恒星以及地面噪声：所有天体如恒星、行星等都会辐射能量。这些噪声能量作用在天线工作范围内就会降低 SNR。

18. 线路损耗：若接收信号的功率很小（例如仅有10^-12 W），该信号就特别容易受噪声的影响。因此在接收机的前端必须特别注意保证噪声足够小，以便能可靠地放大信号。接收天线和接收机前端之间的波导和电缆（馈线）都会造成信号衰减和热噪声。 5.3 小节将详细讨论这个问题。

19. 接收机噪声：即接收机中产生的热噪声， 具体内容在 5.1 小节到 5.4 小节介绍。

20. 实施损耗：这种性能损耗是理论检测性能和实际性能的差值。实际运用中的种种缺陷，例如定时误差、频率偏移、波形的上升下降次数以及有限值的运算等，都会造成与理论值的偏差。

21. 不良的同步参考：若能正确产生载波相位、子载波相位和信号定时参考，差错概率将与《Part 3——基带信号解调与检测》和《Part 4——带通调制和解调》推导的 $E_b/N_0$ 一致。但通常情况下，这些对象并不能完全正确地产生，从而导致系统损耗。

---

3. 接收信号功率和噪声功率

3.1 量程方程

  链路预算的主要目的是检测通信系统能否按计划运行，也就是信息质量（差错性能）能否达到指定要求。链路预算分析出从发射机到接收机的全过程中传输信号的“升”和“降”（增益和损耗）。综合计算接收 $E_b/N_0$ 的大小，满足需求的盈余。计算处理过程由量程方程（range equation）开始，因为量程方程建立了接收功率与发射机和接收机之间距离的函数关系。以下讨论量程方程。

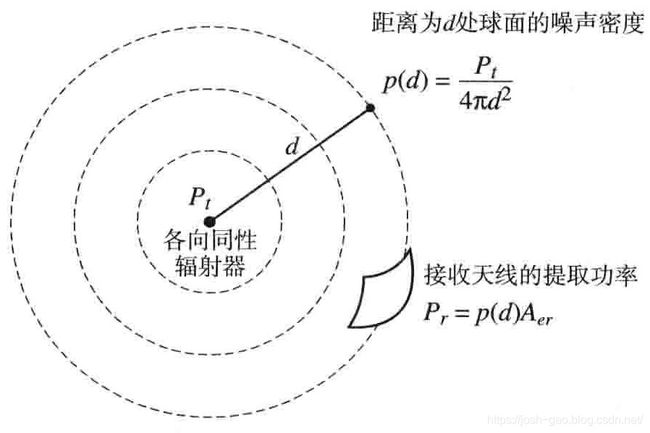
  在无线通信系统中，载波由发射机通过发射天线传输。发射天线是将电信号转化为电磁波的转换器。在接收端，接收天线则执行相反的功能，将电磁波转化成电信号。对发射机和接收机之间基本的功率关系的研究，通常以全方向 RF 源的假设（在 $4\pi$ 球面角度上均匀发射）为基础。此理想源称为 各向同性辐射器（isotropic radiator），如图 5.3 所示。假定球体上功率密度 $p\left(d\right)$（$d$ 是到源的距离）与发射功率 $P_t$ 的关系为（即假设发射功率均匀地分布在整个球面上）
$$p\left(d\right)=\frac{P_t}{4\pi d^2}\mathrm{W}/{\mathrm{m}}^2$$球面面积为 $4\pi d^2$。从接收天线提取的功率为
$$P_r=p\left(d\right)A_{er}=\frac{P_t{A}_{er}}{4\pi d^2}$$其中，参数 $A_{er}$ 是接收天线的吸收剖面（有效面积），定义为
$$A_{er}=\frac{总提取功率}{瞬时功率流量密度}$$

• 如果讨论的天线是发射天线，其有效范围记为 $A_{et}$。
• 如果讨论的天线不能确定是用做接收还是发射，其有效面积则记为 $A_e$。
  
  

图5.3 量程方程（用距离描述接收功率）

  天线的有效面积 $A_e$ 和物理面积 $A_p$ 由效率参数 $\eta$ 相互关联，即
$$A_e=\eta A_p$$上式明总的瞬时功率不能被全部提取，由于各种因素总会有损耗。碟形天线（抛物面反射器）的 $\eta$ 为 0.55，角锥喇叭天线的 $\eta$ 为 0.75。

  表示天线输出（输入）功率与各向同性辐射器功率之间关系的参数（纯几何比）称为天线方向性或方向增益（directive gain），即
$$G=\frac{最大功率密度}{4\pi 球面的平均功率密度}$$

• 如果没有耗散损耗或阻抗失谐损耗，天线增益（在最大强度方向上）可以简单地用上式表示。
• 但是只要存在耗散损耗或阻抗失谐损耗，天线增益等于直接增益与这些损耗的损耗因子的乘积。

本文假定耗散损耗为 0 并且阻抗没有失谐。因此，上式也是天线峰值增益（peak antenna gain），它可以认为是将 RF 流量集中在某个比 $4\pi$ 球面小的限定区域内而产生的结果，如图 5.4 所示。现在定义相对于各向同性辐射器的有效辐射功率（EIRP），它是发射功率 $P_t$ 与发射天线增益 $G_t$ 的乘积，即
$$\boxed{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}=P_t{G}_t}$$

图5.4 天线增益是将各向同性 RF 流量集中的结果

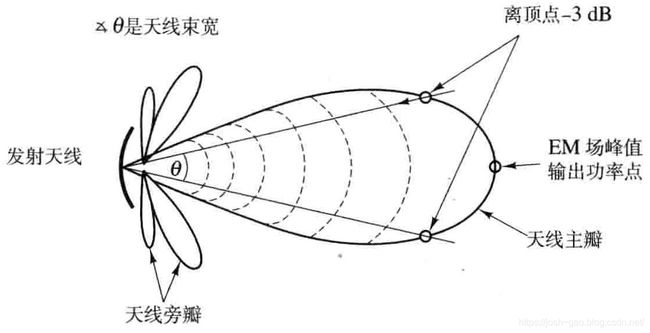
3.1.1 量程方程的基础

  大多数情况下，相对于各向同性天线，发射机具有一些天线增益，用 $\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}$ 代替 $P_t$ 改写式 $P_r=\frac{P_t{A}_{er}}{4\pi d^2}$，有
$$P_r=\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}\frac{A_{er}}{4\pi d^2}$$天线增益 $G$ 和天线有效面积 $A_e$ 的关系式为
$$\boxed{G=\frac{4\pi A_e}{{\lambda }^2}\left(A_e\gg {\lambda }^2\right)}$$其中，$\lambda$ 是载波波长。波长 $\lambda$ 和频率 $f$ 互为倒数关系， 即 $\lambda =\frac{c}{f}$，$c$ 是光速（约为 3 × 10⁸ m/s）。发射天线和接收天线的表达式类似。互易定理（reciprocity theorem）表明，给定天线和载波波长，发射增益和接收增益相等。

  通过天线场视图可以测量集中绝大多数场能量的固定角度，也可以测量天线的方向特性；它与天线增益成反比——高增益的天线与狭窄的场视图相对应。通常我们不采用固定角度场视图测量方法，而采用以弧度或角度为单位的平面波束宽度（beamwidth）。图 5.4 描述了方向天线模式，说明了天线束宽的一般定义。束宽指从最大场功率下降 3 dB 的角度。

  接下来讨论束宽与频率、天线大小与束宽之间的变化关系。由 $G=\frac{4\pi A_e}{{\lambda }^2}\left(A_e\gg {\lambda }^2\right)$ 可知，

• 天线增益随波长减小（频率增加）而增加；
• 天线增益还随有效面积增大而增加。

增加天线增益等效于将流量密度聚集在更小的圆锥角上，因此无论增大信号频率还是天线大小，都会导致束宽窄化（narrower beamwidth）。

  令 $G=1$ 来计算各向同性天线的有效面积，$A_e$ 为
$$A_e=\frac{{\lambda }^2}{4\pi }$$为了求解接收功率 $P_r$，当接收天线是各向同性时，将上式代入 $P_r=\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}\frac{A_{er}}{4\pi d^2}$ 有
$$P_r=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}}{{\left(4\pi d/\lambda \right)}^2}=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}}{L_s}$$其中，${\left(4\pi d/\lambda \right)}^2$ 称为路径损耗（path loss）或自由空间损耗（free-space loss），用 $L_s$ 表示。注意，上式表明各向同性天线的接收功率等于有效发射功率，它只受路径损耗的影响而降低。如果接收天线不是各向同性的，用 $G_r{\lambda }^2/4\pi$ 取代 $A_e$，可以得到更一般的表达式
$$\boxed{P_r=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}{G}_r{\lambda }^2}{{\left(4\pi d\right)}^2}=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}{G}_r}{L_s}}$$其中，$Q_r$ 为接收天线增益。上式称为量程方程。

3.2 接收信号功率与频率的函数关系

  由于发射天线和接收天线都可以由增益或面积表示，因此，$P_r$ 有如下 4 种表示方法
$$P_r=\frac{P_t{G}_t{A}_{er}}{4\pi d^2}$$$$P_r=\frac{P_t{A}_{et}{A}_{er}}{{\lambda }^2{d}^2}$$$$P_r=\frac{P_t{A}_{et}{G}_r}{4\pi d^2}$$$$P_r=\frac{P_t{G}_t{G}_r{\lambda }^2}{{\left(4\pi d\right)}^2}$$以上表达式中，$A_{er}$ 和 $A_{et}$ 分别是接收天线和发射天线的有效面积。

  在以上四式中，因变量是接收信号功率 $P_r$，自变量有发射功率、天线增益、天线面积、波长和范围。如果波长减少（频率增大）而其他自变量保持不变，接收功率将如何变化？

• 由第一式和第三式可知，$P_r$ 与波长完全无关；
• 由第二式看出，$P_r$ 与波长平方成反比；
• 由第四式看出，$P_r$ 与波长平方成正比。

这些表达式当然不是互相矛盾的。表面的矛盾是因为天线增益和天线面积与波长有关联，如 $G=\frac{4\pi A_e}{{\lambda }^2}\left(A_e\gg {\lambda }^2\right)$。那么，什么时候才可以应用以上四式来确定波长与 $P_r$ 之间的关系呢？

• 如果系统已经设计好，即天线已建好，大小确定（$A_{er}$ 和 $A_{et}$ 确定），则可应用第二式计算 $P_r$ 性能。

第二式表明，对大小确定的天线来说，接收功率随波长的减少而增加。

  在第一式中，$G_t$ 和 $A_{er}$ 是自变量，但在求 $P_r$ 关于波长的变化范围时，希望固定 $G_t$ 和 $A_{er}$。当自变量 $\lambda$ 减小时，若发射天线的，由 $G=\frac{4\pi A_e}{{\lambda }^2}\left(A_e\gg {\lambda }^2\right)$ 知 $G_t$ 增加。但是根据假定条件 $G_t$ 固定，所以第一式中的 $G_t$ 不能增加。换言之，为确保在波长减小时 $G_t$ 不变，需减小发射天线的大小。显然

• 第一式适用于发射天线增益（或束宽）固定而参数 $A_{et}$ 不定的情况。

类似地，

• 第三式适用于 $A_{er}$ 和 $G_r$ 固定的情况，
• 第四式适用于发射天线和接收天线增益（或束宽）固定的情况。

  图 5.5 说明卫星的一种应用：要求下行链路天线束能够提供全球稷盖（同步高度上束宽约为 17°）。由于卫星天线增益 $G_t$ 必须固定，由第一式可知 $P_r$ 与波长无关。如果在频率 $f_1\left(=c/{\lambda }_1\right)$ 上提供全球覆盖，若频率切换成 $f_2$，$f_2>f_1$ 覆盖率将下降（对给定天线，$G_t$ 增加）；因此必须减小天线的大小以保证覆盖率或束宽。可以看出，覆盖全球的天线在载波频率增加时，需要减小尺寸。

图5.5 接收功率作为频率的函数

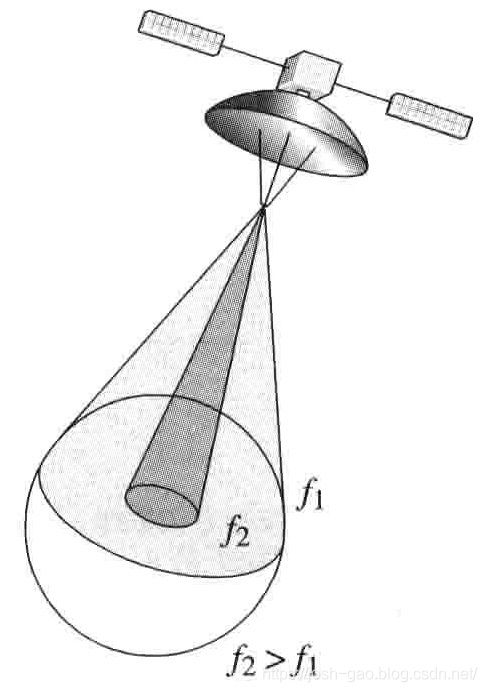
3.3 路径损耗与频率的关系

  由 $L_s={\left(4\pi d/\lambda \right)}^2$ 可知，路径损耗 $L_s$ 与波长（频率）相关。路径损耗（它只是几何上的平方倒数损耗）为什么是频率的函数？$P_r=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}}{L_s}$ 中的路径损耗是对各向同性接收天线（$G_r=1$）的预测。因此，路径损耗能简便地预测各向同性接收天线的功率损耗。

  从几何意义来说，图 5.3 和 $p\left(d\right)=\frac{P_t}{4\pi d^2}\mathrm{W}/{\mathrm{m}}^2$ 指出功率密度 $p\left(d\right)$ 是距离的函数，而与频率无关。由于路径损耗的推算基于 $G_r=1$，计算各向同性天线（isotropic antenna）的 $P_r$ 值与 $P_r=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}}{L_s}$ 类似。再次强调一下，$L_s$ 可以看做所有称为路径损耗（path loss）的项的集合。这个命名描述了纯粹的几何效果，而忽略了对 $G_r=1$ 的基本要求，将其称为单位增益传播损耗（unity-gain propagation loss）更恰当。在无线通信系统中，路径损耗是信号功率中最大的损耗。卫星系统中，对同步高度上 C 波段（6 GHz）的链路的路径耗损一般为 200 dB。

3.4 热噪声功率

  所有导体中电子热运动都会产生热噪声。热噪声在天线与接收机之间以及接收机第一级的有损耦合中产生。热噪声功率谱密度在频率 10¹² Hz 以下为常数，所以称为白噪声。在《Part 1——信号和频谱》的 5.5 小节中已描述，通信接收机将热噪声过程看成加性高斯白噪声（AWGN）。热噪声或散粒噪声的物理模型是开路均方电压为
$$4kT°WR$$的噪声发生器，其中

• $k$ 是玻尔兹曼常数，其值为 $1.38\times 10^{-23}\text{J/K 或 W/K - Hz}=-228.6\text{ dBW/K - Hz}$
• $T°$ 表示温度，单位是开尔文
• $W$ 表示带宽，单位是 $\text{Hz}$
• $R$ 表示电阻，单位是 $\Omega$

  由噪声发生器耦合到放大器前端的热噪声功率最大值为
$$N=kT°W\text{W}$$所以，放大器输入端的最大单边噪声功率谱密度 $N_0$（1 Hz 带宽内的噪声功率） 为
$$N_0=\frac{N}{W}=kT°\text{W/Hz}$$  表面看来噪声功率与电阻大小有关，但其实两者无关。从直觉上就可以说明这一点。在电路中将大电阻与小电阻相连，大小电阻形成闭合通路，它们的物理温度相同。若噪声功率是电阻的函数，那么将有从大电阻流向小电阻的净功率流，大电阻变凉而小电阻变热。这个假设违背实际经验，与热力学第二定理冲突。因此，从大电阻传送给小电阻的功率必与其接收的功率相等。

  由 $N=kT°W$ 可知，热噪声的可实现功率与噪声源周围的温度（噪声温度，noise temperature）有关。因此引入一个有用概念：噪声源的有效噪声温度（effective noise temperature）并不是噪声源（例如星系、大气、干扰信号）进入接收天线的必要热量。噪声源的有效噪声温度定义为能产生相同干扰功率的热噪声源估计温度。噪声温度的内容将在 5.5 小节中详细介绍。

---

4. 链路预算分析

  在评估系统性能时，由于主要考虑的是在可接受差错概率下对含噪信号的检测能力， 所以最重要的参数是信噪比（SNR）或 $E_b/N_0$。在卫星通信系统中，最常用的信号结构是包络不变的已调制载波，这时可以将平均载波功率 / 噪声功率（carrier power-to-noise power，$C/N$）之比作为检波前的 SNR。在实际应用中，对包络不变的信号，检波前的 SNR 可以表示为
$$\frac{P_r}{N}\equiv \frac{S}{N}\equiv \frac{C}{N}\equiv \frac{C}{kT°W}$$其中，$P_r$，$S$，$C$ 和 $N$ 分别是接收功率、信号功率、载波功率和噪声功率；$k$、$T°$、$W$ 分别是波尔兹曼（Boltzmann）常数、开尔文温度和带宽。$P_r/N$ 或 $S/N$ 并不总是与 $C/N$ 相等， 信号功率和载波功率只在包络不变时（角调制）才相等。例如，用调制消息波形 $m\left(t\right)$ 表示的调频（FM）载波， 表达式为
$$s\left(t\right)=A\cos \left[{\omega }_{0}t+K\int m\left(t\right)\text{d}t\right]$$其中，$K$ 是系统常量。调制信号的平均功率是 $\overline{m^2\left(t\right)}$。增加调制功率只会增加 $s\left(t\right)$ 的频率偏移，这说明载波的频谱得到拓展，但平均功率 $\overline{s^2\left(t\right)}$ 与调制信号的功率变化无关，仍保持 $\frac{A^2}{2}$ 不变。所以，FM（包络不变）信号具有接收信号功率与载波功率相等的特点。

  对于线性调制，如幅度调制（AM），调制信号的功率与载波功率不同。例如，分析调制信号为 $m\left(t\right)$ 的 AM 载波：
$$s\left(t\right)=\left[1+m\left(t\right)\right]A\cos {\omega }_{0}t$$$$\overline{s^2\left(t\right)}={\left[1+m\left(t\right)\right]}^2\frac{A^2}{2}=\frac{A^2}{2}\left[1+\overline{m^2\left(t\right)}+\overline{2m\left(t\right)}\right]$$假定 $m\left(t\right)$ 的均值为 0，则平均载波功率为
$$\overline{s^2\left(t\right)}=\frac{A^2}{2}+\frac{A^2}{2}\overline{m^2\left(t\right)}$$由上式可知， 此例中载波功率与信号功率不同。简言之，对于包络不变信号（如 PSK 、FSK），参数 $C/N$ 和 $P_r/N$ 相同，而对于包络变化信号（如 ASK、QAM）则不同。

  将 $P_r=\frac{\mathrm{E}\mathrm{I}\mathrm{R}\mathrm{P}{G}_r}{L_s}$ 除以噪声功率 $N$ 得到 $P_r/N$
$$\frac{P_r}{N}=\frac{\text{EIRP}{G}_r/N}{L_s}$$上式可应用于任何单向 RF 链路。

• 若采用模拟接收机（analog receiver），解调噪声带宽（通常指有效或等效噪声带宽）往往比信号带宽大，$P_r/N$ 是测量信号的可检测性和性能质量的主要参数。
• 若采用数字接收机（digital receiver），则通常采用相关器或匹配滤波器并使得信号带宽与噪声带宽相等。

数字链路通常的处理模式是用噪声功率谱密度（noise power spectral density）代替噪声功率。用 $N_0=\frac{N}{W}=kT°$ 重写上式，有
$$\boxed{\frac{P_r}{N_0}=\frac{\text{EIRP}{G}_r/T°}{k{L}_s{L}_o}}$$其中系统有效温度 $T°$ 是辐射到天线的噪声和接收机第一级产生的热噪声两者共同作用的结果。

接收天线增益 $G_r$ 和系统温度 $T°$ 组合为一个整体 $G_r/T°$，有时称为接收机的品质因数（figure-of-merit）。6.2 小节将介绍这些术语。

  值得强调的是，有效温度 $T°$ 是建模各种噪声源的参数，这部分内容将在 5.5 小节详细介绍。上式中引入了术语 $L_o$， 用来表示其他损耗和 $\frac{P_r}{N}=\frac{\text{EIRP}{G}_r/N}{L_s}$ 中未说明的其他降损因子。可以用因子 $L_o$ 对不同损耗和噪声源的种类做大的分类。上式概括了所有链路分析的关键参数：

• 接收信号功率与噪声功率谱密度之比（$P_r/N$）；
• 有效各向同性辐射功率（EIRP）；
• 接收品质因数（$G_r/T°$）；
• 损耗（$L_s$，$L_o$)。

  下面介绍分析通信链路记录增益和损耗的方法。首先应用
$$\frac{P_r}{N_0}=\frac{\text{EIRP}{G}_r/T°}{k{L}_s{L}_o}$$由功率源计算到达检测端（检前点）的净 SNR。这类似于商业“记账”系统，记录资产、负债、利润（或亏损）的底线。上式就相当于这样的一个企业形式。

• 所有分子参数（有效辐射功率，接收品质因数）就像企业的资产，
• 所有的分母参数（热噪声、空间损失、其他损耗）则像企业的负债。

  假定调制（信息承载）信号包含了所有的接收功率 $P_r$，由《Part 3——基带信号解调与检测》得到的 $E_b/N_0$ 和 SNR 的关系式
$$\frac{E_b}{N_0}=\frac{P_r}{N}\left(\frac{W}{R}\right)$$$$\frac{E_b}{N_0}=\frac{P_r}{N_0}\left(\frac{1}{R}\right)$$以及
$$\boxed{\frac{P_r}{N_0}=\frac{E_b}{N_0}R}$$其中，$R$ 是比特速率。如果部分的接收功率是载波功率（信号功率损耗），除非载波功率会影响损耗因子 $L_o$，否则都可以应用上述 $E_b/N_0$ 和 SNR 的关系式。在设计和评估系统时，经常会用到上述 $E_b/N_0$ 和 SNR 的基本关系（见 Part 9）。

4.1 两个重要的 $E_b/N_0$ 值

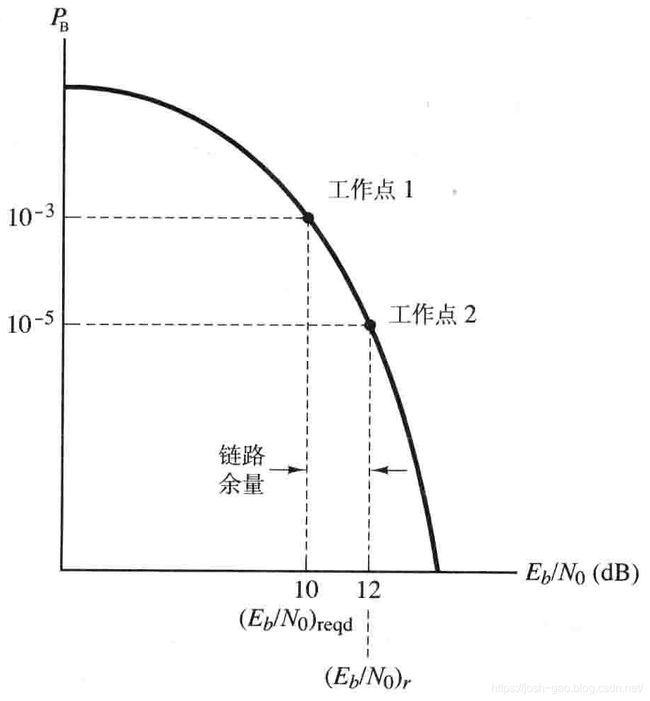
  $E_b/N_0$ 是指为了获得一定的差错概率而需要的比特能量与噪声功率谱密度之比。为了便于计算余量或安全因子 $M$，需要获得所需 $E_b/N_0$ 与实际 $E_b/N_0$（或接收 $E_b/N_0$）的差值。因此，将前者表达为 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}$，将后者表达为 ${\left(E_b/N_0\right)}_r$。图 5.6 描述了一个具有两个工作点的例子。一个点的 $P_B=10^{-13}$，这是系统所需差错性能的工作点。假定 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}=10\text{ dB}$ 就可以得到所需的性能。能否建立一个系统以使解调器刚好能接收到 10 dB? 显然不行。应该设计一个具有安全余量的系统，使得实际接收的 ${\left(E_b/N_0\right)}_r$ 大于 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}$。所以设计的系统，其工作点应该是图 5.6 的另一个点。这时 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}=12\text{ dB}$，$P_B=10^{-5}$。在这个例子中，我们可以将安全余量或链路余量（link margin）表示为能提供 2 次幕的 $P_B$ 改善；或者换用更常用的说法，我们可以用提供比所需的 $E_b/N_0$ 大 2dB 的 $E_b/N_0$ 来描述链路余量。用链路余量参数 $M$ 来改写 $\frac{P_r}{N_0}=\frac{E_b}{N_0}R$ 有
$$\frac{P_r}{N_0}={\left(\frac{E_b}{N_0}\right)}_{r}R=M{\left(\frac{E_b}{N_0}\right)}_{\text{reqd}}R$$链路余量就是 ${\left(E_b/N_0\right)}_r$ 和 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}$ 的差值（dB）
$$M\left(\text{dB}\right)={\left(\frac{E_b}{N_0}\right)}_{\text{reqd}}-{\left(\frac{E_b}{N_0}\right)}_r\left(\text{dB}\right)$$参数 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}$ 反映了不同系统设计间的差别；这些差别可能是由于调制或编码方式的不同而导致的。在次最佳 RF 系统中，可能需要采用比 ${\left(E_b/N_0\right)}_{\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{d}}$ 大的 $E_b/N_0$，因为这时会出现较大的定时误差，或者在检测过程中有比理想匹配滤波器中更多的噪声出现。

图5.6 两个重要的 E_b/N₀ 值

  联立
$$\{\begin{array}{l}\frac{P_r}{N_0}=\frac{\text{EIRP}{G}_r/T°}{k{L}_s{L}_o}\\ \frac{P_r}{N_0}={\left(\frac{E_b}{N_0}\right)}_{r}R=M{\left(\frac{E_b}{N_0}\right)}_{\text{reqd}}R\end{array}$$ 得到链路余量 $M$：
$$\boxed{M=\frac{\text{EIRP}{G}_r/T°}{{\left(E_b/N_0\right)}_{\text{reqd}}Rk{L}_s{L}_o}}$$上式称为链路余量方程（link margin equation），它包括了所有影响链路差错概率的参数， 某些参数是根据特定的链路位置定义的。例如，

• $E_b/N_0$ 定义在接收机的输入端，更精确地说，应该是定义在检测器的输入端（检前点），这里，系统判决的基础是解调波形的电压幅度与接收能量成正比。类似地，用于描述接收能量或功率的参数，无论是有用的还是有害的，都是在检前点定义的。
• 接收机品质因数 $G_r/T^{°}$ 定义在接收天线的输入端，$G_r$ 是接收天线的增益，$T°$ 是有效系统温度（见 5.5 小节）。
• 有效辐射功率 $\text{EIRP}$ 定义为发射天线输出端的电磁波功率。

参数 $E_b/N_0$、$G_r/T^{°}$ 和 $\text{EIRP}$ 都定义于特定的系统位置。

4.2 链路预算的分贝形式

  由于链路预算分析通常以分贝为单位，因此将上节提出的链路余量方程表示为
$$\begin{array}{rl}M\left(\text{dB}\right)=& \text{EIRP}\left(\text{dBW}\right)+G_r\left(\text{dBi}\right)-{\frac{E_b}{N_0}}_{\text{reqd}}\left(\text{dB}\right)-R\left(\text{dB-b/s}\right)\\ & -k{T}^{°}\left(\text{dBW/Hz}\right)-L_s\left(\text{dB}\right)-L_o\left(\text{dB}\right)\end{array}$$

• 发射信号功率 $\text{EIRP}$ 的单位为分贝瓦（$\text{dBW}$）；
• 噪声功率谱密度 $N_0$ 的单位为分贝瓦 / 赫（$\text{dBW/Hz}$）；
• 天线增益 $G_r$ 是以分贝为单位以各向同性增益（$\text{dBi}$）为参照的增益；
• 数据速率 $R$ 表示为 $1\text{ b/s}$ 的分贝值（$\text{dB-b/s}$）；
• 其他参数的单位都为 $\text{dB}$ 。

上式参数值构成了链路预算，它是分配通信资源的有效工具。在维持正的余量值的前提下，可以在各种参数之间进行权衡。例如，

• 通过放弃过多的余量来减小发射功率；
• 通过降低 ${\left(E_b/N_0\right)}_{\text{reqd}}$（通过改进调制和编码方式）来增加数据速率。

上式所有的分贝参数一律都是 $\text{dB}$ 量。发射系统“不知道也不关心”这些 $\text{dB}$ 的来源。只要接收机的 $E_b/N_0$ 符合要求，就可以达到期望的系统差错性能。同时为达到差错性能还需具备两个条件——实现同步，最小化或均衡 ISI 失真。大家可能会问，既然系统不知道 $E_b/N_0\text{ dB}$ 值的来源，如何获得充足的 $\text{dB}$ 值？答案是，寻找最高性价比的 $\text{dB}$ 值。这个目标促使了纠错编码的诞生。为提高差错性能，采用纠错编码可以减少电子设备的投入。

4.3 链路余量的充足值

  系统设计时需要多少链路余量？如果所有的增益、损耗和噪声源都已严格设计（最坏情况），并且具有较大方差的链路参数（比如天气造成的衰落）能达到链路可用性的统计需求，那么只需要很小的额外余量。所需的余量取决于各部分链路预算的可信度，如采用新技术或新工作频率的系统，比已经反复构建和测试的系统需要更多的余量。有的时候，链路预算允许直接将天气引起的衰落作为一个线性项；不过其他时候，所需余量值则反映了降雨影响性能时的链路需求。对于在 C 波段（上行链路为 6 GHz，下行链路为 4 GHz）上运行的卫星通信系统，假设所有参数已知而且正常工作，可能只需要 1 dB 的链路余量。只用于接收的电视台使用直径为 16 英尺（1 英尺 = 0.304 8 m）、运行在 C 波段的碟形卫星天线，设计的余量往往比 1 dB 小得多。但是标准为 99.9% 可靠度的卫星电话系统需要相当大的余量； 一些 INTELSAT 系统需要 4~5 dB 的余量。当计算基于一般情况而不是最坏情况时，通常允许各单元设备在工作温度范围、线性电压偏差和工作时间范围内变化。同样，对于空间通信，也允许跟踪卫星定位出现误差。

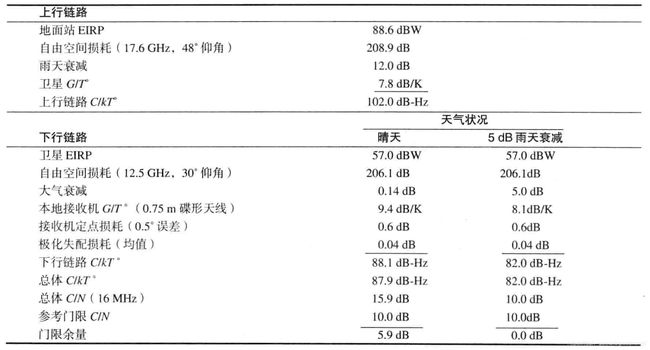
  使用较高频率（ 如 14/12 GHz）的设计时，通常需要更大的（天气）余量，这是因为大气损耗随频率增加而且较易变化。注意，由于天线损耗导致的衰减副产物要比天线噪声大。对低噪声放大器而言，小的天气变化会导致天线温度 40~50 K 的增加。表 5.1 是卫星电视公司（Satellite Television Corporation）向 FCC 提交的用于提供 DBS 服务的链路分析。注意，下行链路预算列出两种天气条件的选择：晴天和衰减为 5 dB 的雨天。

• 晴天时，由天气衰减造成的信号损耗远小于 1 dB，
• 雨天时，最大信号损耗可达 5 dB。

下行链路表中下一项的本地接收机 $G_r/T°$ 是因降雨造成的额外降级；扩散到接收天线的附加热噪声造成系统有效噪声温度增加，而使本地接收机 $G_r/T°$ 减小（从 9.8 dB/K 到 8.1 dB/K )。因此， 在增加天气损耗额外余量的同时，要加大补偿系统噪声温度增加的额外余量。

表5.1 卫星电视公司提供的卫星直播（DBS）链路分析

  对于卫星链路，常有“链路能够闭合”和“链路不能闭合”的说法：

• “链路能够闭合”的意思是以分贝为单位的余量值是一个正值并且能满足所需的差错性能，
• “链路不能闭合”的意思是余量值为负值，不能满足所需的差错性能。

虽然“链路闭合”和“链路不闭合”的说法有“开－关”条件的意思，但是它强调的是，链路不闭合或负的余量值意味着差错性能不能达到系统需求，而并不指停止通信。例如，分析这样一个系统， ${\left(E_b/N_0\right)}_{\text{reqd}}=10\text{ dB}$，${\left(E_b/N_0\right)}_r=8\text{ dB}$ 如图 5.6 所示。假定 $8\text{ dB}$ 对应于 $P_B=10^{-2}$，因而有 $-2\text{ dB}$ 的余量，差错概率约是指定差错概率的 10 倍。链路的性能虽然降低但仍是可用的。

4.4 链路可用率

  链路可用率是基于年平均的对链路长期使用状况的衡量；对于给定的地理位置，链路可用率是指链路闭合时间的百分比。例如，对于华盛顿区到卫星中继器间的指定链路，长期天气模型是 $10\text{ dB}$ 的余量足以使得 $98\%$ 时间内链路闭合，而 $2\%$ 时间内暴雨造成了 $10\text{ dB}$ 以上的 SNR 降级，因此链路不能闭合。因为降雨对 SNR 降级的影响与信号频率有关，链路可用性与所需的余量必须根据特定发射频率而定。

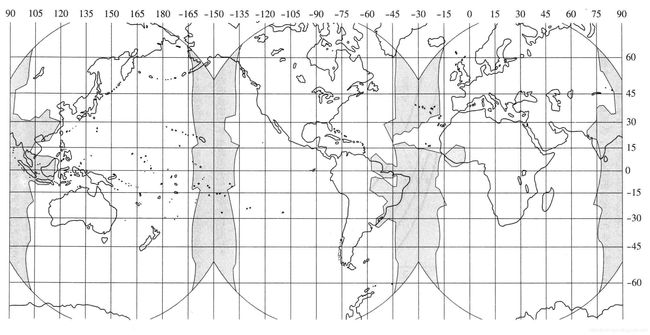
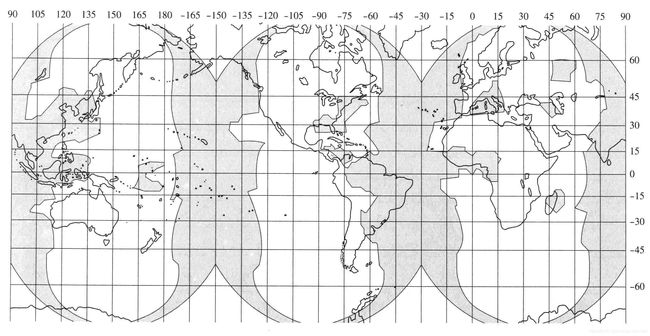
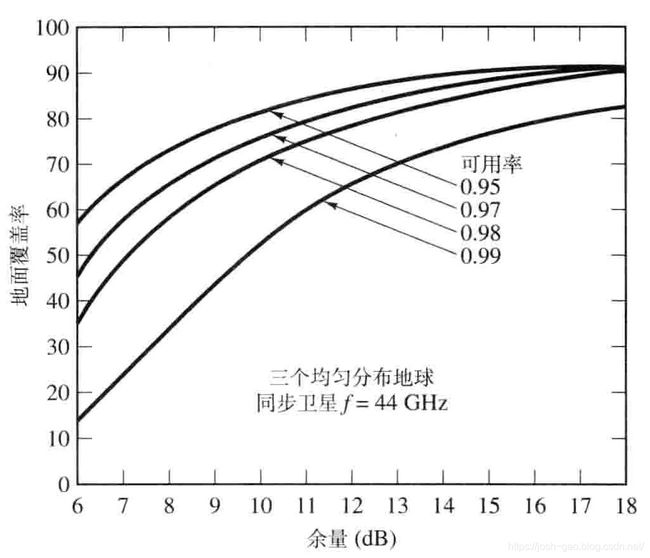
  图 5.7 总结了 44GHz 频率时全球范围卫星链路的可用率。该图描绘了在采用三个等空间分布、地球同步卫星情况时，地面投盖率百分比（链路闭合，达到指定差错概率）对余量的函数关系。卫星位于 35 800 km 的同步高度上， 轨道与地球赤道在同一平面上。卫星轨道的周期与地球自转的周期相同，因此从地面看卫星的位置似乎是固定的。图 5.7 展示了不同链路可用率的狻盖率曲线族，从良性（可用率为 $95\%$) 到完全合格（可用率为 $99\%$) 。一般地，若固定链路余量，覆盖率与所需的可用率成反比； 若固定链路可用率，覆盖率随余量单调上升。图 5.8 至图 5.10 描绘了在 44GHz 频率时三个不同余量链路的闭合情况，非阴影和阴影区域对应于链路在 $99\%$ 时间上闭合和不闭合的区域。图 5.8 表示余量值为 $14\text{ dB}$ 的链路覆盖范围。注意，该图可用于大降雨地区，如巴西和印尼，其结果考虑到了地球气候模型的影响。

图5.7 不同链路可用率的地面覆盖率与链路余量的关系曲线

  在图 5.8 中， 每个卫星场视图的东部和西部都出现了阴影条纹。为什么这些区域达不到要求的链路可用率？这是因为在地球的边缘处，卫星与地面之间的传播路径要比卫星下面的直接路径远。有三种降级因素：

1. 较远的路径引起接收天线功率密度的减少；
2. 覆盖区边缘的卫星天线增益减少，除非卫星天线被设计成整个场视图内增益一致的模式（典型模式是边缘增益比射束中心增益降 3 dB）;
3. 由于路径的倾斜和地球的曲度，到达地球边缘的传播需要经过更厚的大气层。

第 3 项是在最易受大气衰减影响的信号频段上的关键因素。为什么图 5.8 中南极和北极区域没有阴影部分？因为降雪不会像降雨那样给信号传输造成有害影响，这种现象称为冻结效应（freeze effect）。

  图 5.9 描绘了 44 GHz 频率时链路余量为 $10\text{ dB}$ ，在 $99\%$ 时间上闭合和不闭合的地面区域。可以看到，与 $14\text{ dB}$ 余量的情况相比，该图中的阴影区域明显增大；美国的东海岸、地中海和日本的大部分地区在 $99\%$ 时间上链路不能闭合。图 5.10 描绘了余量为 $6\text{ dB}$ 的类似的链路性能。与图 5.8 能够用于最大降市地区不同，图 5.10 适于天气最干燥的地区，这些地区有美国的西南部、澳大利亚的大部分地区、秘鲁和智利的海岸以及非洲的撒哈拉沙漠。

图5.8 链路可用率为 0.99 时三个等空间分布、地球同步卫星的地面覆盖率（非阴影部分），f = 44 GHz，链路余量为 14dB

图5.9 链路可用率为 0.99 时三个等空间分布、地球同步卫星的地面稷盖范围（ 非阴影部分），f = 44 GHz, 链路余量为 10dB

图5.10 链路可用率为 0.99 时三个等空间分布、地球同步卫星的地面覆盖范围（非阴影部分） ，f = 44 GHz，链路余量为 6dB

---

5. 噪声系数、噪声温度和系统温度

5.1 噪声系数