数据结构中常用的排序算法总结

0x00相关概念

1.排序

通常在排序的过程中需要进行两个基本操作：
（1）比较两个关键字的大小。
（2）将记录从一个位置移动到另一个位置。

2.算法稳定性

有一个待排序序列，里面有两个相同的值，假设都是39，为了好区分，一个记为39，另一个记为39 。
假设在排序前，39在39 的前面，如果使用了一个排序算法以后，39仍然在39 以前，那么这个算法就是稳定的；如果使用了排序算法以后39在39前面，那么这个算法就是不稳定的。

3.内部排序&外部排序

在排序的过程中，根据数据元素是否始终完全在内存中，可以把排序算法分成两类，即内部排序和外部排序。

内部排序：在排序期间元素全部存放在内存中。
外部排序：在排序期间元素无法全部同时存放在内存中，必须根据要求不断的在内存和外存之间移动。

内部排序主要关注如何使算法的时间复杂度和空间复杂度更低，而外部排序除了关注这些以外，还需要关注如何使读写磁盘的次数更少。

0x01外部排序

1.插入排序

插入排序的基本思想：每次将一个待排序的记录按其关键字的大小插入前面已排好序的子序列，直到全部记录插入完成。

（1）直接插入排序

算法思想：
设待排序序列L[1…n]，在某次的排序过程中，前 i-1 个元素是有序序列，中间的元素 L[ i ] 是此次排序将要确定位置的元素，i+1到n是无序序列。
1.先查找出要排序的元素 L[ i ] 在前面有序序列中的位置k。在确定位置的时候，将 L[ i ] 先与 L[ i-1 ] 比较，再与 L[ i-2 ] 比较，也就是从后往前比较。
2.将 k 到 i-1 中的元素依次后移一个位置。（在实际的代码实现时，可以边比较边移动，也就是比较一个元素移动一个元素，反复把已排序元素逐步向后挪位。 ）
3.将 L[ i ] 复制到 L[ k ]。
在实现排序时，开始可将 L[ 1 ] 看成是一个已经排好的有序序列，然后将 L[ 2 ] 到 L[ n ] 依次插入到前面已经排好的序列中，一共执行 n-1 次操作就能全部排好。

性能：
通常是就地排序，所以空间复杂度是 o(1)。
平均时间复杂度是 o(n²)。
是一个稳定的算法。适用于顺序表和链表。

（2）折半插入排序

算法思想：
直接插入排序，第一步在有序序列中确定新元素的位置时，是将新元素与有序序列的元素，从后往前依次比较来确定位置的，边比较边移动。折半插入排序就是在第一步确定位置的时候，采用折半查找（二分法）来确定新元素的待插入位置，然后统一的后移待插入位置之后的所有元素。

性能：
通常是就地排序，所以空间复杂度是 o(1)。
时间复杂度是 o(n²)。
是一个稳定的算法。适用于顺序表。

（3）希尔排序

算法思想：
1.先将整个待排序序列分割成若干子序列，如：L[ i , i+d , i+2d ,…i+kd ] ，即把相隔某个增量的记录组成一个子表。假设此时的步长为 d₁ 。
2.在每个子序列内进行直接插入排序。
3.再取一个步长，假设为d₂（d₂1）。重复上面两个步骤，直到取步长为1，即所有记录已经放在同一组中，再进行直接插入排序。
注意：希尔提出的步长是 d₁=n/2，d₂=d₁/2，并且最后一个步长为1。

性能：
通常是就地排序，所以空间复杂度是 o(1)。
时间复杂度依赖于增量序列，是个还没解决的数学难题。最坏情况下是o(n²)，也就是直接取步长为1，即直接插入排序。
是一个不稳定的算法。适用于顺序表。

2.交换排序

交换排序思想：根据两个元素关键字的比较结果来对换两个记录再序列中的位置。

（1）冒泡排序

算法思想：
从后往前或者从前往后，依次比较相邻的两个元素，若为逆序则交换他们，直到序列比较完，称为一趟冒泡排序。
冒泡排序的特征是每完成一趟冒泡排序，都至少会有一个元素出现在它最终应该出现的位置上。最多n-1趟冒泡就能把所有元素交换。

性能：
通常是就地排序，所以空间复杂度是 o(1)。
平均时间复杂度是 o(n²)。
是一个稳定的算法。适用于顺序表和链表。

（2）快速排序（重要）

算法思想：
1.在待排序序列中选取一个枢轴元素pivot（或基准，通常是首元素）。
2.通过一趟快速排序以后，会将待排序序列划分成三个部分：左边部分 L[1…k-1]，中间 L[ k ]是一开始选定的枢轴元素pivot，右边部分 L[k+1 …n]。使得左边部分的元素都小于等于pivot，右边的元素都大于等于pivot。这个过程叫做一趟快速排序。
3.再分别对左边部分和右边部分重复上述过程，直到整个序列有序。
快速排序也是一趟可以确定一个元素的最终位置。与冒泡排序不同的是，冒泡排序中每轮确定的元素的位置是从序列的一端渐渐的向另一端移动的，而快速排序是无序的分布在序列之中的。

一趟快速排序的过程如下：

设置三个指针，一个pivot是枢轴元素，一般选首元素，一个是low指针，指向第一个位置，high指针指向最后一个位置。
因为最后要得到的是左边小于pivot，右边大于pivot的序列，所以思想就是将右边小的元素换到左边，将左边大的元素换到右边。
1.high指针从后往前依次搜索，找到第一个小于pivot的元素交换到low的位置，也就是37与56交换，下图的样子：

2.low指针从前往后依次搜索，找到第一个大于pivot的元素交换到high的位置，也就是85与56交换，下图样子：

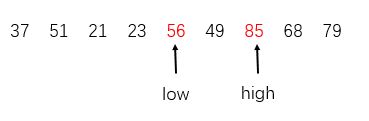
3.再重复第一步，high往前找第一个小于pivot的元素，与low交换，也就是49与56交换：

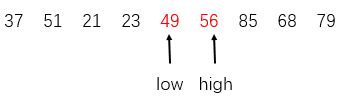
4.再重复第二步，low往后找，此时low再往后一位就等于high了，就算完成了一趟快速排序：

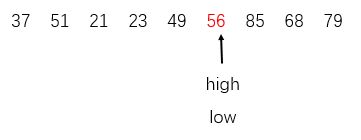
可以看到high（high=low）之前的元素都小于56，之后的元素都大于56.
总结一下一趟快速排序的过程：high往前找到第一个比枢轴元素小的元素，就和low交换位置；low往后找到第一个比枢轴元素大的元素，就和high交换位置；low和high是交替移动的，直到最后low=high，就算一趟完成。

性能：
空间复杂度：快排是递归的，所以需要一个递归工作站来保存信息，容量与递归调用的深度一致。平均空间复杂度是o(log₂n)。
时间复杂度：平均情况是o(nlog₂n)。
快排是一个不稳定的排序方法。适用于顺序表。

3.选择排序

（1）简单选择排序

算法思想：
将待排序的序列分成三部分，前 i-1 个元素是已经排好的，第 i 个元素是当前需要排的，第 i+1 到第 n 个元素是还没有排序的。
每次排序的时候从第 i+1 到第 n 个元素中选择出最小的元素与第 i 个元素交换位置，在选择最小的元素的时候需要进行 n-i 次关键字的比较。一共需要n-1 趟可以使整个序列有序，不管原先是逆序还是顺序，都需要进行 n-1 趟。

性能：
空间复杂度：o(1)。
时间复杂度：最好，最坏和平均都是o(n²)。因为比较次数与初始状态无关，比较次数始终为 n*(n-1)/2 。
移动次数最好的情况是0次，最多不会超过 3*(n-1) 次。
适用于顺序表和链表，是不稳定的算法。

（2）堆排序

算法思想：
分为大根堆和小根堆。大根堆：所有的子树中父结点大于左右孩子结点，所以根节点是最大的元素，大根堆排序生成的是降序的。小根堆：所有的子树中父结点小于左右孩子结点，所以根节点是最小的元素，小根堆生成的是升序的。
所以堆排序的过程就是：输出根节点，堆底元素送入堆顶，调整堆，输出根节点，堆底元素送入堆顶上，调整堆，不断的重复。
堆的调整：对大根堆来说就是小元素不断下坠的过程。对小根堆来说就是大元素不断下坠的过程。每个结点下坠一层的时候，需要对比关键字一次或者两次，如果这个结点只有一个孩子的话，则需要对比一次，如果这个结点有两个孩子的话，则需要对比两次，先让两个孩子比较，再让孩子与下坠元素之间进行比较。
建堆：长度为n的序列对应n个结点的完全二叉树。最后一个非终端结点的序号是 n/2(向下取整) ，该序号往后都是叶子节点。
堆的插入：每次插入的元素都先放在堆的末端，然后再进行堆的调整。

性能：
空间复杂度：o(1)。
时间复杂度：建堆o(n)，堆的调整o(log₂ⁿ)。堆排序的最好，最坏和平均情况都是o(nlog₂ⁿ)。
堆排序适用于顺序表，是个不稳定的算法，适合关键字较多的情况。

4.归并排序

算法思想：
归并排序是将两个或两个以上的有序表组合成一个新的有序表。m路归并就是将m个子表合并成一个有序表，每选出一个元素需要对比 m-1 次关键字。
假设是个2路归并，一个子表长度是len1，一个子表的长度是len2，那么进行2路归并的时候，关键字比较次数最少是min{len1,len2}，最多是len1+len2-1。

性能：
空间复杂度：o(n)，因为需要一个辅助数组。
时间复杂度：一趟是o(n)，一共需要 log₂ⁿ 趟，所以时间复杂度是o(nlog₂ⁿ)。

5.基数排序

算法思想：
基于关键字各位的大小进行排序，又分为最高位优先法（百位–>十位–>个位）和最低位优先法（个位 -->十位–>百位）。
如果基数是10，也就是十进制的数，则需要借助十个队列，十个队列分别对应0，1，2，3，4，5，6，7，8，9。既然是队列，就符合先进先出的原则。以高位优先法为例，先比较各个元素的最高位，假如是百位，百位是1就进入1对应的队列，百位是6就进入6对应的队列，将所有元素按照百位分好队了以后，将所有元素输出生成新的序列，注意队列的性质是先进先出，所以输出的时候不要乱了顺序。接着进行十位的排序，同样的原理，最后进行个位的排序。

性能：
空间复杂度：假设一趟需要r个队列，则整个算法的空间复杂度就是 o®，因为这些队列下一趟还可以重复使用。
时间复杂度：设整数的位数是d，一共有n个元素，基数是r，则一共需要进行d趟的收集与分配，分配的时间复杂度是 o(n)，收集的复杂度是 o®，
所以一共是 o(d(n+r))。
基数通常基于链式存储，是个稳定的算法。

0x02外部排序

1.外部排序的方法

外部排序通常使用归并排序。
k路归并就是在内存中设置k个输入缓冲区，1个输出缓冲区，缓冲区的大小和磁盘块的大小是相同的，因为计算机读写的时候是以磁盘块为单位的。
归并的过程其实可以看做一棵树，所以r个初始归并段进行k路归并的时候需要进行的趟数为 log_k^r(向上取整)，即树高。
外部排序的总时间=内部排序所需的时间+外存信息读写时间+内部归并时间。

2.败者树

败者树可以减少比较的次数，本质上是一个完全二叉树，但是比完全二叉树还多了一个最上面的结点，也就是最后的胜利结点。
败者树的内部结点记录的是失败的段号，让胜者继续比较。

3.置换选择排序

置换选择排序是用来生成初始归并段的，可以减少初始归并段的数量，最后会得到不同长度的归并段。
要注意算法的过程中会不断的更新MINMAX。

4.最佳归并树

最佳归并树其实是个哈夫曼树，每次选择最小的几个元素作为孩子结点，他们的和是父节点的值，将这个新生成的结点参与到下一次的选择中。需要注意的是，需要增加虚段，因为有的时候段的数量不足，虚段就是值为0的结点。
假如有a个初始归并段，需要构成一个k叉树，则 (a-1)%(k-1)=u ，如果u=0则不需要增加虚段，如果u不等于0，则需要添加 k-u-1 个虚段。