炸雷(详细解析)
问题描述
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下, 在一个二维平面上放置着 nn 个炸雷, 第 ii 个炸雷 \left(x_{i}, y_{i}, r_{i}\right)(xi,yi,ri) 表示在坐标 \left(x_{i}, y_{i}\right)(xi,yi) 处 存在一个炸雷, 它的爆炸范围是以半径为 r_{i}ri 的一个圆。
为了顺利通过这片土地, 需要玩家进行排雷。玩家可以发射 mm 个排雷火 箭, 小明已经规划好了每个排雷火箭的发射方向, 第 jj 个排雷火箭 \left(x_{j}, y_{j}, r_{j}\right)(xj,yj,rj) 表 示这个排雷火箭将会在 \left(x_{j}, y_{j}\right)(xj,yj) 处爆炸, 它的爆炸范围是以半径为 r_{j}rj 的一个圆, 在其爆炸范围内的炸雷会被引爆。同时, 当炸雷被引爆时, 在其爆炸范围内的 炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?
你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个 炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
输入格式
输入的第一行包含两个整数 n 、 mn、m.
接下来的 nn 行, 每行三个整数 x_{i}, y_{i}, r_{i}xi,yi,ri, 表示一个炸雷的信息。
再接下来的 mm 行, 每行三个整数 x_{j}, y_{j}, r_{j}xj,yj,rj, 表示一个排雷火箭的信息。
输出格式
输出一个整数表示答案。
样例输入
2 1
2 2 4
4 4 2
0 0 5
样例输出
2
样例说明
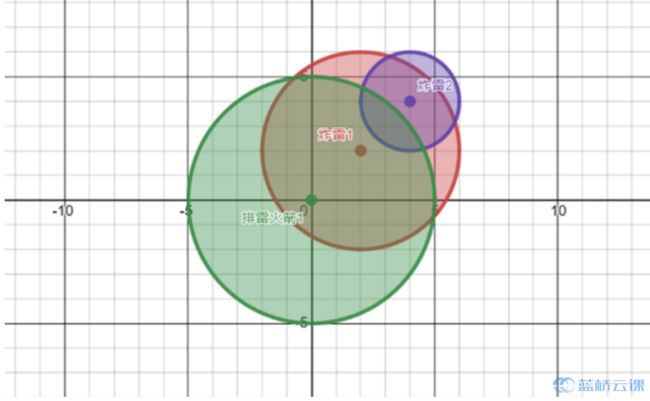
示例图如下,排雷火箭 1 覆盖了炸雷 1,所以炸雷 1 被排除;炸雷 1 又覆盖了炸雷 2,所以炸雷 2 也被排除。
评测用例规模与约定
对于 40 %40 的评测用例: 0 \leq x, y \leq 10^{9}, 0 \leq n, m \leq 10^{3}, 1 \leq r \leq 100≤x,y≤109,0≤n,m≤103,1≤r≤10.
对于 100 %100 的评测用例: 0 \leq x, y \leq 10^{9}, 0 \leq n, m \leq 5 \times 10^{4}, 1 \leq r \leq 100≤x,y≤109,0≤n,m≤5×104,1≤r≤10.
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
解题过程
一开始的暴力算法40分
#define _CRT_SECURE_NO_WARNINGS
#include
#include
int main()
{ int a[10000][10]={0};//雷
int b[10000][10]={0};//排雷
int n,m,count=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=3;j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=3;j++)
{
scanf("%d",&b[i][j]);
}
}
for(int k=1;k<=m;k++)
{
for(int i=1;i<=n;i++)//这个需要每一个雷区的认真排查,你把循环逻辑想清楚,不要靠记忆!
{
if(a[i][4]!=1)
{
// if((a[i][1]-b[i][1])*(a[i][1]-b[i][1])+(a[i][2]-b[i][2])*(a[i][2]-b[i][2])<=(b[k][3]*b[k][3]))
if((a[i][1]-b[k][1])*(a[i][1]-b[k][1])+(a[i][2]-b[k][2])*(a[i][2]-b[k][2])<=(b[k][3]*b[k][3]))
//对应排雷和它的半径想好再写
{
count++;
a[i][4]=1;//标记
}
}
}
}
//自爆
for(int i=1;i<=n;i++)//不认真分析乱写全错,用定一动一法则
{
for(int j=i;j
哈希AC解题过程
#include
using namespace std;
typedef long long ll;//要;
//c++用typedef
ll x, y, r;//写在全局一点问题都没,
//定义的结构体还是函数算重开的,不会有冲突。
int n, m;
const int N = 50010, M = 999997;//使用M的时候要固定用const!
const ll Z = (1e9 + 1);
ll h[M];
ll id[M];
bool st[M];
struct circle
{
ll x, y, r;
}cir[N];//炸雷50000就够了
ll get_v(ll x, ll y)
{
// return x*(1e9+1)+y;err
//数字爆了要加ll,或者自己开一个变量
//加ll必须是一串数字,所以说要这么写就要写成变量
return x * Z + y;
}
ll find(ll x, ll y)
{
ll key = get_v(x, y);
ll t = (key % M + M) % M;
// while(h[t]!=0&&h[t]!=key)初始化写的-1
while (h[t] != -1 && h[t] != key)
{
if (++t == M)
t = 0;
}
return t;
}
ll sqr(ll x)
{
return x * x;
}
// ll dfs(ll x,ll y,ll r)err
void dfs(ll x, ll y, ll r)
//这里只是标记数组,不需要返回类型
{
st[find(x, y)] = true;
for (ll i = x - r; i <= x + r; i++)
for (ll j = y - r; j <= y + r; j++)
//又把j写成i可以啊你,又开始飘了,又调了半天青光眼
{
if (sqr(i - x) + sqr(j - y) <= sqr(r))
{
ll t = find(i, j);
if (id[t] && !st[t])
{
dfs(i, j, cir[id[t]].r);
}
}
}
}
int main()
{
cin >> n >> m;
// meset(h,-1,sizeof h);
memset(h, -1, sizeof h);
// for(int i=0;i>cir[i];err
//先插入x,y,r.再放进数组中
cin >> x >> y >> r;
cir[i] = { x,y,r };
ll t = find(x, y);
if (h[t] == -1)
{
h[t] = get_v(x, y);
}
if (!id[t] || cir[id[t]].r < r)
{
id[t] = i;//如果i从0开始,这样就相当于没有赋值。
}
}
while (m--)
{
cin >> x >> y >> r;//火箭的坐标直接扔了是吧?
for (ll i = x - r; i <= x + r; i++)
for (ll j = y - r; j <= y + r; j++)
//又把j写成i可以啊你,又开始飘了,又调了半天青光眼
{
if (sqr(i - x) + sqr(j - y) <= sqr(r))
{
// int t=find(x,y);
//是i和j不是x,y!写代码麻烦带脑子
ll t = find(i, j);
if (id[t] && !st[t])
//id直接判断是否真值不是!=0
{
dfs(i, j, cir[id[t]].r);
}
}
}
}
int res = 0;
for (ll i = 1; i <= n; i++)
{
if (st[find(cir[i].x, cir[i].y)])
res++;
}
cout << res;
return 0;
}
//以后总是超时记得看下循环条件,尤其注意i和j!
//long long不会成为超时的理由,相反ll虽然内存比int 大,但是比int快很多,而且内存大的才一点点
//题目中的内存永远是足够大的
//所以如果想开ll,就随便开,没必要可以判断,反而时间还更短了!
//怕溢出就干脆写多点ll
详解
//核心是哈希
//哈希算法就相当于把没有规律的值,通过他们的一些信息储存在数组中
// 当然处理的手法必须保证下标不会冲突重复
//然后一旦要用到这个数组的某个数据,输入相关信息,再从哈希函数中找就能找到对应下标然后使用了.
//就是使用数据本身的一些特征信息来建立桥梁,每次访问下标就通过访问函数即可获取.
//因为题目的每一个数据都是对应下标产生的,当你想要通过范围寻找坐标判断对应的点的时候
//你又很难找到这个点究竟在哪个数据中
//如果直接无脑插入数组,每一次的检测判断所有的地雷1e5,地雷与地雷,地雷和排雷,必超时
//所以说必须要用哈希直接对应坐标快速查找才能实现AC
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 50010, M = 999997;//十倍的N效果最好,而且质数更好3,7//哈希表长度
//防总是冲突要设大十倍最理想,但是总要比你无脑建立数组来的时间短,再怎么存我存1e5的数据也只用1e6
int n, m;
struct Circle
{
int x, y, r;
}cir[N];//炸雷
//坐标最好建立结构体统一最好
LL h[M];
//哈希数组:存放哈希值,相当于标记该位置已经被占用,当前下标不可用,是为find找下标服务的
// 同时也是作为返回该下标的标志,即哈希值相同时直接返回这个坐标实现快速查找
// 哈希的核心是找下标
//哈希数组有什么优势吗?相比顺序存储
// 它可以提供非常快速的插入-删除-查找操作
// 无论多少数据,插入和删除需要接近常量的时间:即O(1)的时间级。实际上,只需要几个机器指令即可完成。
// 哈希表的速度比树还要快,基本可以瞬间查找到想要的元素
// 哈希表相对于树来说编码要容易很多
//但就是没有顺序
int id[M];// id数组为哈希数组中cir对应的哈希地雷下标
bool st[M];// 判断是否访问过
LL get_key(int x, int y)
//求哈希值:返回每一个不同坐标的唯一结果
{
return x * 1000000001ll + y;
//在1e9+1进制上
// xy: 第二位 第一位
//如,1,0/0,1/,不同坐标必须有一个操作确定唯一的值
//核心就是不要让x,y的不同坐标得出相同的答案.
//只要在数字后加类型就能直接附上类型,这么写防止溢出
//最大上限是10^9,
//这么写是为了确定唯一性
//为何一定要这么大,小了时间更高?
//必须是这么写,改小了超时
//哈希值:xy总体看成一个(1e9 + 1)进制数字,
//可以将(x,y)看作是一个数字,即xy,因为x,y最大为10^9,所以只要看成看成一个(1e9 + 1)进制数字
//就可以完美的固定x,y的结果,一定有唯一值,因为y永远不会进位,x永远在y的前面,所以结果永远不同.
//这样即使y为最大的10^9,它同样无法进位,一直在第一位上,而第二位也是一样,每次满1e9+1进1位,
//同样第二位最终也是10^9无法到达第三位,但已经确定了每个x,y对应的唯一值,
//如果进制低了,y就可以进位,这样就没有办法肯定x,y一定有唯一值,答案就不准确了
//这么写就确保y一直在第一位,x一直在第二位.形象于1e9+1进制的数字xy.y永远在后面,
//就确定了xy的唯一结果
//唯一确定的位置,即每次返回的结果不同,这是重点
//当然最低限度是范围+1,你可以任意选择这以上的任何进制作为你的哈希值,
//只要x,y能分开.
//总结:根据数字范围确定进制分割x,y!确定唯一值的核心在于让一个数位上的值永远无法进位即可.
//不进位就不会有多个值.
}
int find(int x, int y)//寻找哈希值
//快速查找的根源在于与x,y坐标建立联系
//我们很清楚坐标的大小,但是我们却不清楚它具体储存在数组的位置
//所以通过x,y与数组位置联系起来,我们就能很轻松的访问想要的数组
//而不是一个个遍历
{
LL key = get_key(x, y);//值的大小
int t = (key % M + M) % M;
//给所求的哈希值一个存放的位置.
//而设大数组是防止总是冲突
//这么存是尽可能均匀
//%M是为了找在数组中的哪一个位置对应存放
//+M%M是防止是负数的转正操作(因为没有负数下标)
// 如果该位置已经被占用并且不等于我们要求的哈希值,要在之后找到相应位置
while (h[t] != -1 && h[t] != key)
if (++t == M)//遍历+尽头时从头走过
t = 0;
//判断该位置是否有赋值过,防止冲突
//有赋值过并且不是自己想要的结果key的
//我们就往下找,直到找到结果key为所需下标
//函数的两用:有就要找看看是否哈希值对应,
//没有赋值表示没有冲突,我直接把x,y对应到这个t下标(最理想的结果)
return t;//返回存放下标
}
int sqr(int x)
{
return x * x;
}
void dfs(int x, int y, int r)
{
st[find(x, y)] = true;//标记引爆的炸雷
for (int i = x - r; i <= x + r; i++)
for (int j = y - r; j <= y + r; j++)
if (sqr(i - x) + sqr(j - y) <= sqr(r))
{
int t = find(i, j);
if (id[t] && !st[t])
dfs(i, j, cir[id[t]].r);
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
//初始化哈希数组
for (int i = 1; i <= n; i++)//炸雷
{
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
cir[i] = { x, y, r };
//这个数组是为了最后输出结果遍历使用的
//是地雷总数,没有被哈希处理过的原始数据
//作用, 存储所有数据
// 因为可能有同坐标地雷的存在,而标记法只对一个数据生效,所以说必须要开一个数组来记录所有数据
// 如果没有同坐标,那么完全就不用cir数组
int t = find(x, y);//找对应x,y的哈希值的数组下标
if (h[t] == -1)
h[t] = get_key(x, y);//哈希值的存放到h[t]
//哈希数组就是为了存放炸雷的坐标
//好处,不用浪费太多的数组空间,
//达成什么目的?可以用数组干嘛啊哈希?
//数组设太大会超时,而且也不允许设这么大
if (!id[t] || cir[id[t]].r < r)
//初始没有赋值的数组一定是假的
// id数组没有被标记或者找到了同一个坐标点更大半径的地雷
//(就挺阴间的,同坐标还可能有多个雷,三个阴间测评数据)
id[t] = i;
//地雷是随机插入的,
//就是利用哈希来确定所需地雷的位置
//所以id的作用就是用哈希对应地雷的下标.
//插入哈希炸雷+更换为最大的一个雷
}
//统一使用t下标就是为了将这些数据同时调用,不用查找
//相当于一条线将所有需要用的数据串联起来
//一旦我求出了这个t,那么这些值我都能直接拿起来用,
while (m--)//火箭,每一种火箭的遍历
{
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
for (int i = x - r; i <= x + r; i++)
// 从(x-r, y-r)枚举到(x+r, y+r),圆不好枚举,枚举矩形
for (int j = y - r; j <= y + r; j++)
if (sqr(i - x) + sqr(j - y) <= sqr(r))//枚举火箭范围中有没有炸雷
//表示坐标在圆内
//(x- a)²+(y-b)²=r²
//圆的方程不是面积!
// 表示坐标为(a,b)的圆心
// 你不熟悉可以改循环为x,y,但是与题目设置冲突不太好
// 你套公式就对了
//枚举多一点没什么大碍
{
int t = find(i, j);
//寻找哈希位置下标,直接调用所有数据
//?//当前坐标的导入
//寻找哈希值
//像这里,我们可以直接根据坐标来很快锁定对应数据的位置
//然后直接导出对应位置,比你直接插入数组无法根据特征判断位置输出
//想要的结果快多了
if (id[t] && !st[t])
// 如果该点有地雷,没有被访问过,能被炸到
//这里是顺着题目思路写下去的,火箭引爆炸雷
//炸雷接连引爆其他炸雷,深度搜索。
dfs(i, j, cir[id[t]].r);
}
}
int res = 0;
for (int i = 1; i <= n; i++)
if (st[find(cir[i].x, cir[i].y)])//炸雷总数
//寻找所有的雷中炸了的
//输入cir时输入进了所有的炸雷,包括同坐标的。
//前面替换了哈希的炸雷也没关系,因为只要是同坐标被标记
//那么每次遍历到相同的坐标时也一样是为真值继续加一,
//这就是为什么要替换成最大半径,
//只要这个最大范围的炸雷都炸了,那在里面的炸雷也同样会炸,
// 而且只有最大范围的炸雷才是准确的炸雷与扎雷的搜索
//可以直接重复加入同坐标这样的一个操作.
res++;
printf("%d\n", res);
return 0;
}