【数据可视化】案例一：美国人口与种族变迁史

实验介绍

        作为一个移民国家，美国的种族和人口问题全方位地影响着美国各州的政治、经济、文化和司法，本实验通过对美国人口普查局与美国国家卫生统计中心自 1990 以来调查获得的长达 29 年的美国人口和种族数据的分析，研究及可视化了美国在此期间的人口和种族的变迁史。

知识点

• 散点图接口及其参数的使用
• 漏斗图的绘制
• 画布上多子图的绘制
• 散点图的数据拟合
• 颜色条的绘制和应用
• 数据对数变换技巧

---

        输入并执行魔法命令 %matplotlib inline， 同时将全局字体大小设置为 20 号，设置显示负数，去除图例边框、右侧坐标轴、顶部坐标轴。

import warnings
import matplotlib.pyplot as plt
%matplotlib inline

# 屏蔽代码运行过程中出现的警告信息，主要是屏蔽 pandas 的 .loc 警告问题
warnings.filterwarnings("ignore")

# 将全局字体大小设置为 20 号
fontsize = 20
plt.rcParams['xtick.labelsize'] = fontsize
plt.rcParams['ytick.labelsize'] = fontsize
plt.rcParams['axes.labelsize'] = fontsize
plt.rcParams['axes.titlesize'] = fontsize
plt.rcParams['legend.fontsize'] = fontsize

plt.rcParams['legend.frameon'] = False  # 去除图例边框
plt.rcParams['axes.unicode_minus'] = False  # 显示负数
plt.rcParams['axes.spines.right'] = False  # 去除右侧坐标轴
plt.rcParams['axes.spines.top'] = False  # 去除顶部坐标轴

数据准备

数据集介绍：

        本数据集来源于美国人口普查局与美国国家卫生统计中心，该数据集统计了美国自 1990 至 2019 年期间，各年度全美 51 州各年度性别（Gender）、种族（Race）、年龄段（Age Group）的人口数（Population），数据集中的 Mean Age 字段根据 Age Group 求算术平均得到。

导入数据并查看前 5 行。

import pandas as pd

df = pd.read_csv('https://labfile.oss.aliyuncs.com/courses/3023/American_Race_Gender_Population.csv')
df.head()

	Age Group	State	Gender	Race	Year	Population	Mean Age
0	1-4	Alabama	Female	American Indian or Alaska Native	1990	419.0	2.5
1	1-4	Alabama	Female	American Indian or Alaska Native	1991	445.0	2.5
2	1-4	Alabama	Female	American Indian or Alaska Native	1992	379.0	2.5
3	1-4	Alabama	Female	American Indian or Alaska Native	1993	344.0	2.5
4	1-4	Alabama	Female	American Indian or Alaska Native	1994	352.0	2.5

各州各种族人口数分布

        本实验主要用到的可视化对象为散点图，散点图是继条形图后，用作描述性统计、数据挖掘、数据预测的第二大类可视化图形，图元素主要包括点的位置，点的形状和点的大小。

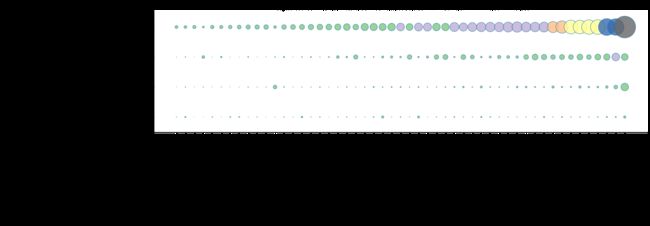
        选择 1990 和 2019 两个年份，将数据集按照州（State）、种族（Race）进行人口数（Population）聚合并按照人口数升序排序。聚合后，将聚合数据集中的 State、Race 特征分别映射至散点图 x、y 坐标，将 Population 人口数特征映射至点的颜色（c）和大小（s）。

plt.rcParams['figure.figsize'] = (20, 5)  # 图像显示大小

for year in [1990, 2019]:
    data = df.loc[df['Year'] == year]  # df.loc() 根据行/列的标签进行查询

    # 各州按照总人口数升序排序
    state_order = data.groupby(['State'])[  # 按列State进行分组，按Population数据列的和进行升序排序
        'Population'].sum().sort_values().index    # 取出排序后的序号
    # 将 State 字段设置为有序字段
    data['State'] = data['State'].astype(   # astype函数用于将数据类型转换成指定类型。
        pd.api.types.CategoricalDtype(state_order, ordered=True))
# pandas.api.types.CategoricalDtype(categories = None, ordered = None) :该类对于指定独立于数值的分类数据的类型很有用，有类别和顺序。

    # 获取州、种族的聚合结果，并按州升序排序 
    data = data.groupby(['State', 'Race'], as_index=False)[ # 按列'State', 'Race'进行分组，求出人口总数，按State数据列的和进行升序排序
        'Population'].sum().sort_values(['State'])

    plt.scatter(
        x=data['State'],  # x轴为州
        y=data['Race'],   # y轴为种族
        c=data['Population'],           # 点的颜色，按人口的多少来划分
        s=data['Population']*0.0001,    # 点的大小：根据画出来的图的情况进行调节
        ec='tab:blue',       # 
        cmap=plt.cm.Accent,  # cmap相当于多个调色盘的合集。当选取一个色盘（viridis）后，从参数c获取到的数值，映射到色盘对应的颜色上。
        alpha=0.8)   # alpha：散点的透明度（[0, 1]之间的数，0表示完全透明，1则表示完全不透明）。

    ax = plt.gca()  # gca()进行坐标轴的移动
    ax.tick_params(axis='x', rotation=90) # 将x轴刻度标签逆时针旋转90度  
    ax.set_ylim(-0.5, 3.5) # 调节y轴显示范围

    plt.title('Population Distribution of States of American in Year %d' % year)
    plt.show()  # 关闭当前图层以绘制下一幅图

 从输出结果可以看出：

• 各州人口数。根据 2019 年统计数据，美国人口数最多的三个州分别为 California、Texas、Florida；
• 种族人口数。美国人口种族分布上，白人（White）显著地占据着主体地位，排名第二的种族为 黑人（Black or African American），随后是亚裔（Asian or Pacific Islander）；
• 各州人口变迁。对比 1990 年与 2019 年，按照人口数排序后的 x 轴，可以发现 29 年间，美国各州表现出不同速率的人口增长率，1990 年总人数排名第二的 New York 已悄然在 2019 年排名第四。

人口与人口增长率

        提取数据集中 1990 和 2019 两年的数据，通过数据透视计算各州人口增长率（Pupulation Changed %），通过数据聚合计算各州 2019 年总人口数（Population），将上述分步计算结果合并并挑选需要的特征后查看前 5 行。

# 取出指定列'Year'的1990和2019数据
data = df.loc[(df['Year'] == 1990) | (df['Year'] == 2019)]   

# 计算美国各州人口增长率
pop_change = data.pivot_table(
    index='State', columns='Year', values='Population',aggfunc='sum')
# values：要做计算的数据 ，对谁求和/求均值/计算个数等
# index：确定行参数，可以是多个。单个’‘，多个[’‘,’‘]表示
# columns：确定列参数，可以是多个。单个’‘，多个[’‘,’']
# aggfunc：要计算的函数，mean求均值、sum求和、size计算个数
pop_change['Pupulation Changed/%'] = 100 * \            # 加上一列'Pupulation Changed/%'
    (pop_change[2019]-pop_change[1990])/pop_change[1990]
pop_change

# 计算美国2019年各州总人口数
pop = df.loc[df['Year'] == 2019].groupby(['State'])['Population'].sum()

# # 将人口增长率与白人增长率数据合并并筛选需要的特征
data = pd.concat([pop, pop_change], axis=1)[    # 在列上做合并
    ['Population', 'Pupulation Changed/%']]

data.head()

State	Population	Pupulation Changed/%
Alabama	4903185.0	21.064652
Alaska	731545.0	32.217282
Arizona	7278717.0	97.571264
Arkansas	3017804.0	28.058301
California	39512223.0	31.885389

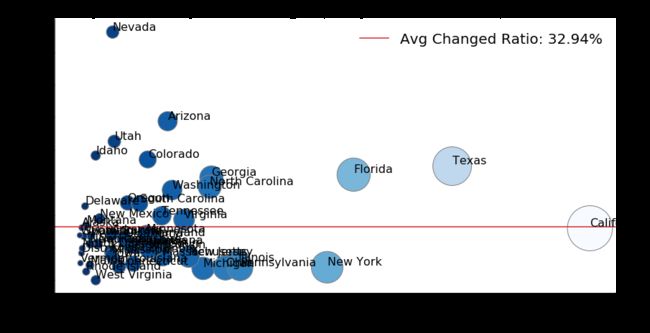
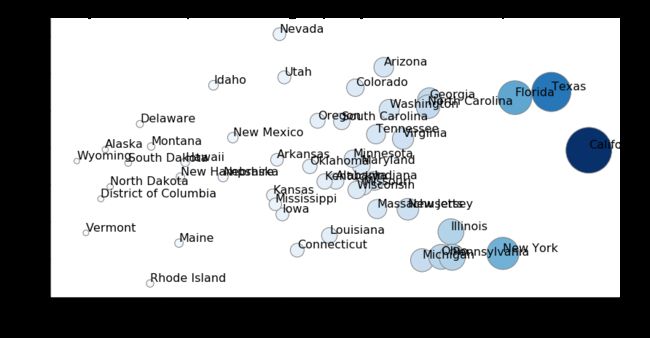
将人口总数与人口增长率数据分别映射到散点图 x、y 坐标及点颜色和大小。

plt.rcParams['figure.figsize'] = (14, 7)  #  # 图像显示大小（长, 宽）
 
x = data['Population']            # x变量
y = data['Pupulation Changed/%']  # y变量

plt.scatter(x, y,
            marker='o',                  # 点的形状
            s=data['Population']*0.0001, # 点的大小
            c=data['Population'],        # 点的颜色
            cmap=plt.cm.Blues_r,         # 调色板，与c配合使用
            edgecolors='gray')  # 散点图标记的轮廓及填充颜色

plt.xlabel('Population')
plt.ylabel('Pupulation Changed /%')
# 画均值线
plt.axhline(y=y.mean(),color='tab:red',label=f'Avg Changed Ratio:{y.mean():.2f}%')

plt.legend()   # 添加图例

s = data.index # 取出索引

for xpos, ypos, text in zip(x, y, s):    # 将坐标（x,y）和索引（州）打包然后遍历
    plt.text(xpos, ypos, text, size=16,va='bottom',ha='left')  # 设置文字说明

plt.title('Population & Pupulation Changed (Compared to Year 1990) of American') # 设置标题

 从输出结果可以看出：

• 全美各州在 1990 - 2019 年间的人口平均增长率为 32.94%；
• 在人口最大的四个州中，Califonia 人口增长率与平均水平相当，Texas 与 Florida 有了超平均数的增长，而 New York 不出意外地没有达到平均增长率；
• 在人口增速方面 Nevada 和 Arizona 两州有着最好的表现。

        对于人口数量较少和人口增速不明显的多数州，其数据被压缩至平均线以下的 0 轴附近，可通过将数据进行对数变换（log）的方法，将数据均匀分布。

import numpy as np

plt.rcParams['figure.figsize'] = (14, 7)

x = np.log(data['Population'])            # 将数据进行对数变换（log）
y = np.log(data['Pupulation Changed/%'])  # 将数据进行对数变换（log）

plt.scatter(x, y,
            marker='o',
            s=data['Population']*0.0001,
            c=data['Population'],
            cmap=plt.cm.Blues,
            label='Changed of States of American',
            edgecolors='gray')  # 散点图标记的轮廓及填充颜色

plt.xlabel('log (Population)')
plt.ylabel('log (Pupulation Changed /%)')


s = data.index

for xpos, ypos, text in zip(x, y, s):
    plt.text(xpos, ypos, text, size=16, va='bottom', ha='left')

plt.title('Population & Pupulation Changed (Compared to Year 1990) of American')

从输出结果可以看出，数据在对数坐标系下，分散变得十分均匀，各数据点被均匀拉开。

种族及人口变化率

白人

通过以下代码计算各州人口增长率与白人增长率，计算原理与总人口增长率计算原理相同。

# 在原表中指定列'Year'的1990和2019数据
data = df.loc[(df['Year'] == 1990) |(df['Year'] == 2019) ]

# 计算美国各州人口增长率
pop_change=data.pivot_table(index='State',columns='Year',values='Population',aggfunc='sum')# 数据透析表:列为年份，1990和2019两列
pop_change['Pupulation Changed/%']=100*(pop_change[2019]-pop_change[1990])/pop_change[1990]# 在原表新增一列人口变化率
pop_change

# 计算美国各州白人人口增长率
white_change=data.loc[data['Race']=='White'].pivot_table(index='State',columns='Year',values='Population',aggfunc='sum')
white_change['White Changed/%']=100*(white_change[2019]-white_change[1990])/white_change[1990]
white_change

# 将人口增长率与白人增长率数据合并
changed=pd.concat([pop_change,white_change],axis=1) # 将两个表按列合并，共6列

# 挑选主要字段
changed=changed[['Pupulation Changed/%','White Changed/%']]  # 取出'Pupulation Changed/%'和'White Changed/%'两列

# 展示前5行数据
changed.head()

Year	Pupulation Changed/%	White Changed/%
State
Alabama	21.064652	15.051925
Alaska	32.217282	18.947448
Arizona	97.571264	85.805934
Arkansas	28.058301	23.990308
California	31.885389	19.912456

        将各州人口增长率与各州白人增长率分别映射到散点图，通过 np.ployfit 拟合其关系并绘制拟合曲线，同时绘制 y = x 曲线，该曲线表示，种族增长率与人口增长率一致。

plt.rcParams['figure.figsize'] = (10, 6)

x = changed['Pupulation Changed/%']
y = changed['White Changed/%']

# 绘制各州人口及白人增长数据
plt.scatter(x, y,
            marker='o',s=120,
            label='Changed of States of American',
            edgecolors='tab:red',facecolor='white') # 散点图标记的轮廓及填充颜色

plt.xlabel('Pupulation Changed /%')
plt.ylabel('White Race Changed /%')

# 拟合增长率曲线

f_1 = np.polyfit(x, y,deg=1)   # 对（x, y）得到拟合多项式系数f_1，自由度为1

# 绘制 白人人口增长率 拟合的增长曲线
plt.plot(x,np.polyval(f_1, x), # np.polyval(f_1,x)计算多项式的函数值。返回在x处多项式的值，p为多项式系数
         lw=2,color='tab:orange',label='Increase Ratio of White Race') # lw:线宽

# 绘制平衡增长曲线  y=x
plt.plot(np.linspace(0,150,20), # 等差数列：在0~150之间划分20个点；因为线性为“--”，所以这里只是规定了0~150的范围
         np.linspace(0,150,20),
         color='tab:blue',
         label='Increase Ratio of Balance',ls='--',lw=3)

plt.legend()    # 添加图例

# 添加文字说明
plt.text(25,75,'District of Columbia',fontsize=20,color='tab:red',ha='center',va='bottom')
plt.text(155,120,'Nevada',fontsize=20,color='tab:red',ha='center',va='bottom')

plt.title('Population & White Race Changed of States of American')

 

 从输出结果可以看出：

• 种族增长率与人口增长率有很好的线性关系，与 y = x 平衡线对比，白人在各州的增长率斜率小于平衡线斜率（橘色线斜率 < 蓝色线），说明白人增速稍低于平衡增速；
• District of Columbia 州种族增长率显著高于平均水平，白人增速明显。

所有种族

用类似数据处理过程获得全部种族人口增长率与种族增长率数据。

data = df.loc[(df['Year'] == 1990) | (df['Year'] == 2019)]

# 计算美国各州人口增长率
changed = data.pivot_table(index='State', columns='Year', values='Population',aggfunc='sum')
changed['Pupulation Changed /%'] = 100 * \
    (changed[2019]-changed[1990])/changed[1990]


race_columns = ['Pupulation Changed /%']
for race in ['American Indian or Alaska Native', 'Asian or Pacific Islander', 'Black or African American', 'White']:

    # 计算美国各种族人口增长率
    race_change = data.loc[data['Race'] == race].pivot_table(
        index='State', columns='Year', values='Population',aggfunc='sum')   # 数据透析表：两列1990和2019
    race_change[race+' Changed /%'] = 100 * \          # 每次新增一列种族人口变化率
        (race_change[2019]-race_change[1990])/race_change[1990]

    # 将人口增长率与各族人口增长率数据合并
    changed = pd.concat([changed, race_change], axis=1)  

    race_columns.append(race+' Changed /%')    # 加入各种族人口变化率标签
# race_change加入循环前是3列，每个循环都是3列，所以changed总共是15列
# 挑选主要字段
changed = changed[race_columns]  # 取出种族人口变化率标签的那五列

# 展示前5行数据
changed.head()

Year	Pupulation Changed /%	American Indian or Alaska Native Changed /%	Asian or Pacific Islander Changed /%	Black or African American Changed /%	White Changed /%
State
Alabama	21.064652	135.798817	289.331931	31.059229	15.051925
Alaska	32.217282	47.064691	217.124410	58.636664	18.947448
Arizona	97.571264	91.725016	436.006760	270.124184	85.805934
Arkansas	28.058301	178.132082	442.256511	30.806671	23.990308
California	31.885389	167.208411	123.198473	22.854617	19.912456

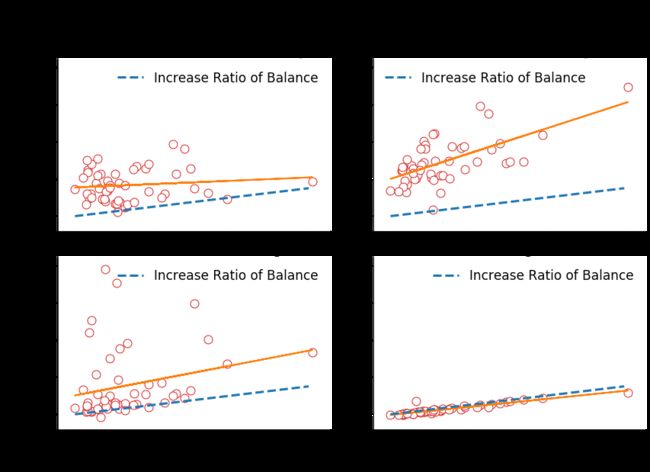
        通过 plt.subplots 接口生成一张画布 fig 和 2 * 2 的子图对象，在每个子图对象分别绘制每个种族的增长率数据。

plt.rcParams['figure.figsize'] = (12, 8)

# 生成 2 * 2 的画布，并共享所有子图x，y轴范围
fig, axs = plt.subplots(2, 2, sharex=True, sharey=True)
# fig代表整个图像，ax代表坐标轴和画的子图，通过下标获取需要的子区域。

axs = axs.ravel()  # 将 2 * 2 的子图对象展平成 1 * 4的子图对象，下面好遍历所有子图

x = changed['Pupulation Changed /%']  # x均为总人口变化率

for i, race in enumerate(race_columns[1:]): # 取出四个种族的人口变化率（除了总人口变化率之外）

    ax = axs[i]        # 遍历每个子图
    y = changed[race]  # y为对应种族的人口变化率

    # 绘制各州人口及白人增长数据
    ax.scatter(x, y,
               marker='o', s=120,     # 散点的形状和大小
               edgecolors='tab:red', facecolor='white')  # 散点图标记的轮廓及填充颜色
    # 拟合增长率曲线
    f_1 = np.polyfit(x, y, deg=1)  # 对（x, y）得到拟合多项式系数f_1，自由度为1（即多项式次数为1）

    # 绘制拟合的增长曲线
    ax.plot(x, np.polyval(f_1, x), # 计算多项式的函数值。返回在x处多项式的值，f_1为多项式系数，元素按多项式降幂排序
            lw=2, color='tab:orange')

    # 绘制平衡增长曲线  y=x
    ax.plot(np.linspace(0, 150, 20),
            np.linspace(0, 150, 20),
            color='tab:blue',
            label='Increase Ratio of Balance', ls='--', lw=3)

    ax.legend(fontsize=17)
    ax.set_title(race,fontsize=17)

    # 第一列和最后一行分别显示y坐标轴标题和x坐标轴标题
    if i in [2, 3]:
        ax.set_xlabel('Pupulation Changed /%')  # 在画第三和第四个图的时候标注x轴标题
    if i in [0, 2]: 
        ax.set_ylabel('Race Changed /%')        # 在画第一和第三个图的时候标注y轴标题

# 添加画布标题
fig.suptitle('Population & Race Changed of States of American\n',
             size=25, va='bottom')

# 调整子图间距为紧凑
plt.tight_layout()

 从输出结果可以看出：

• American Indian or Alaska Native 本土原著名的种族增长率正逐步放缓，其斜率小于平均线；
• Asian or Pacific Islander 亚裔种族增长率为四个种族中最高；
• Black or African American 黑人虽然在增长率上不及亚裔，但在个别州有较为显著增长（图形上表现出大量的偏离拟合曲线点）；
• White 占据人口主要数量的白人与全美总人口增长率大致相当。

通过以下过程，将所有种族人口增长率数据进行纵向拼接。

data = df.loc[(df['Year'] == 1990) |(df['Year'] == 2019) ]

# 计算美国各州人口增长率
changed=data.pivot_table(index='State',columns='Year',values='Population',aggfunc='sum')
changed['Pupulation Changed /%']=100*(changed[2019]-changed[1990])/changed[1990]

race_changes=pd.DataFrame() # 创建二维数组

for race in ['American Indian or Alaska Native', 'Asian or Pacific Islander', 'Black or African American','White']:
    
    # 计算美国各州各种族人口增长率
    race_change=data.loc[data['Race']==race].pivot_table(index='State',columns='Year',values='Population',aggfunc='sum')
    race_change['Race Changed /%']=100*(race_change[2019]-race_change[1990])/race_change[1990]  # 新增一行该种族的人口变化率
    race_change['Race']=race          # 新增一行该种族的名称
 
    # 将人口增长率与各种族人口增长率数据合并
    race_change=pd.concat([changed,race_change],axis=1)       # 按列拼接   
    race_changes=pd.concat([race_changes,race_change],axis=0) # 按列拼接完再进行按行拼接

# 挑选主要字段
race_changes=race_changes[['Pupulation Changed /%','Race Changed /%','Race']]

# 展示前5行数据
race_changes.head()

Year	Pupulation Changed /%	Race Changed /%	Race
State
Alabama	21.064652	135.798817	American Indian or Alaska Native
Alaska	32.217282	47.064691	American Indian or Alaska Native
Arizona	97.571264	91.725016	American Indian or Alaska Native
Arkansas	28.058301	178.132082	American Indian or Alaska Native
California	31.885389	167.208411	American Indian or Alaska Native

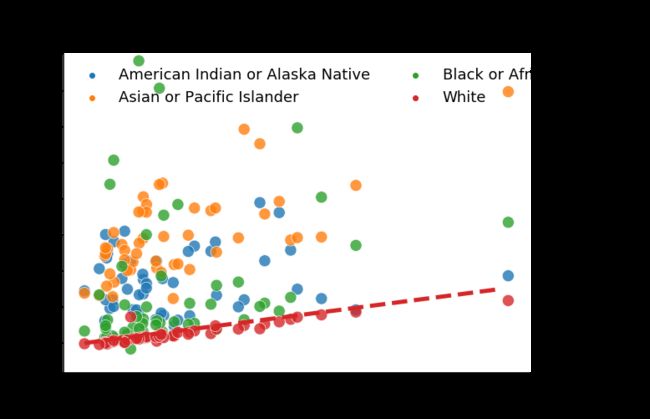
         通过 seaborn 的 scatterplot 接口绘制所有种族的人口增长率与总人口增长率散点图，从输出结果可以看出，该图是将 2 * 2 的子图进行了合并展示，并通过颜色将各种族进行了区分。

import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 7)

sns.scatterplot(
    x='Pupulation Changed /%',
    y='Race Changed /%',
    hue='Race', # 将种族列传入hue，不同种族会输出不同颜色
    s=200,
    alpha=0.8,
    data=race_changes,
)

plt.ylim(-80, 800)
ax = plt.gca()

# 获取图例对象及图例标签对象
h, l = ax.get_legend_handles_labels()
# 第0个图例对象是图例标题，此处将其删除，不显示
ax.legend(h[1:], l[1:], ncol=2, loc=2, fontsize=18)

# 绘制平衡增长曲线  y=x
plt.plot(np.linspace(0, 150, 20),
        np.linspace(0, 150, 20),
        color='tab:red',
        label='Increase Ratio of Balance', ls='--', lw=5)

plt.title('Population & Race Changed of States of American\n',
          size=25, va='bottom')

 从输出结果可以看出：

• 白人增长率数据点与平衡线（红色）分布最为一致；
• 少数族裔相比白人有着较高的人口增长率。

黑人与亚裔

        黑人和亚裔人口增长率有着较为亮眼地表现，以下数据处理过程获得了各州黑人及亚裔的不同增长率。

data = df.loc[(df['Year'] == 1990) | (df['Year'] == 2019)]

# 计算美国各州人口增长率
changed = pd.DataFrame()
race_columns = []
for race in ['Asian or Pacific Islander', 'Black or African American']:

    # 计算美国各州白人人口增长率
    race_change = data.loc[data['Race'] == race].pivot_table(
        index='State', columns='Year', values='Population',aggfunc='sum')
    race_change[race+' Changed /%'] = 100 * \
        (race_change[2019]-race_change[1990])/race_change[1990]

    # 将人口增长率与白人增长率数据合并
    changed = pd.concat([changed, race_change], axis=1)

    race_columns.append(race+' Changed /%')

# 挑选主要字段
changed = changed[race_columns]

# 展示前5行数据
changed.head()

Year	Asian or Pacific Islander Changed /%	Black or African American Changed /%
State
Alabama	289.331931	31.059229
Alaska	217.124410	58.636664
Arizona	436.006760	270.124184
Arkansas	442.256511	30.806671
California	123.198473	22.854617

将各州亚裔和黑人种族人口增长率分别映射到 x、y 将增长率 超 300% 的州用不同颜色进行标记。

plt.rcParams['figure.figsize'] = (15, 8)

x = changed['Asian or Pacific Islander Changed /%']
y = changed['Black or African American Changed /%']

plt.scatter(x, y,
            marker='o', s=120,
            label='Changed of States of American',
            edgecolors='tab:red', facecolor='white')  # 散点图标记的轮廓及填充颜色

plt.xlabel('Asian or Pacific Islander Changed /%')
plt.ylabel('Black or African American Changed /%')


for i in range(len(changed)):
    limit_changed = 300
    # 亚裔增长更快的州
    if (changed.iloc[i, 0] > limit_changed) & (changed.iloc[i, 1] < limit_changed):
        color = 'tab:blue'
    # 黑人增长更快的州
    elif (changed.iloc[i, 1] > limit_changed) & (changed.iloc[i, 0] < limit_changed):
        color = 'tab:red'
    # 亚裔和黑人增长均较快的州
    elif (changed.iloc[i, 1] > limit_changed) & (changed.iloc[i, 0] > limit_changed):
        color = 'tab:orange'
    else:
        color = 'black'

    plt.text(changed.iloc[i, 0], changed.iloc[i, 1], changed.index[i],
             fontsize=20, color=color, ha='center', va='bottom')


plt.title('Asian or Pacific Islander & Black or African American Race Changed of States of American')

 从运行结果可以看出：

• 亚裔增长主要发生在以 Georgia 为代表的蓝色州；
• 黑人增长主要发生在以 Idaho 为代表的红色州；
• 亚裔和黑人在 North Dakota、South Dakota、Nevada 三个州均有较高的增长；
• 亚裔和黑人的增长，在一定程度下，带有一定的地区性特色。

人口结构

各年龄人数随年份变化

将数据集按年份和平均年龄进行聚合，并将年份、平均年龄、人口数映射到散点图。

plt.rcParams['figure.figsize'] = (18, 8)

data = df

# # 获取州、种族的聚合结果，并按升序排序
data = data.groupby(['Year','Mean Age'],as_index=False)['Population'].sum().sort_values(['Population'])

plt.scatter(
    x=data['Year'],
    y=data['Mean Age'],
    c=data['Population'],
    s=data['Population']*0.00003,
    ec='tab:gray',
    cmap=plt.cm.RdBu_r,
    alpha=0.8)

ax = plt.gca()

# 不显示左侧和底部纵坐标轴
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)

# 显示 y 轴网格线
ax.grid(b=True,axis='y',lw=1)

plt.ylabel('Mean Age')

plt.title('Population Distribution of Age Group of American From Year 1990 to Year 2019')

 从运行结果可以看出，美国人口结构正趋向于老龄化，表现在：

• 1990 年：人口结构按年龄组分布，呈现出 20 - 40 岁的单峰分布；
• 2019 年：原先的20 - 40 岁已转移至 40-70 岁年龄组，1990 年以来的新生儿逐渐转移至 20-40 年龄组，呈现出双峰分布。

各年龄组构成的人口结构

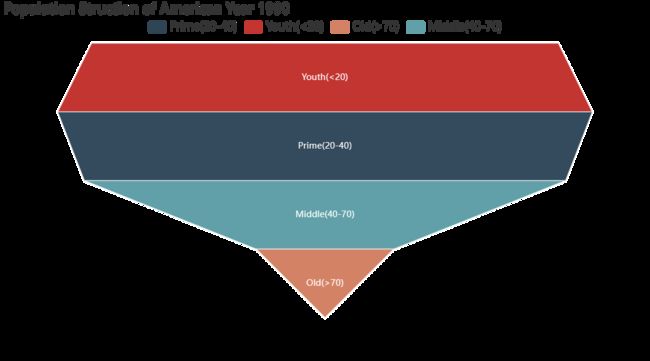
        将平均年龄字段按照 20，40，70 三个节点进行切分，获得 青年、壮年、中年、老年 4 个年龄分组段，聚合各分组段人数后用漏斗图可视化 1990 年的人口结构。

!pip install pyecharts==1.7.1

from pyecharts import options as opts
from pyecharts.charts import Funnel

data = df.loc[df['Year'] == 1990]
# 将平均年龄进行数据切分，生成新的组
data['Age Group3'] = pd.cut(
    data['Mean Age'],
    bins=[0, 20, 40, 70, 100],
    labels=['Youth(<20)', 'Prime(20-40)', 'Middle(40-70)', 'Old(>70)'])
data = data.groupby(['Age Group3'], as_index=False)['Population'].sum()
data['Population'] = data['Population']/np.sum(data['Population'])*100

funel = Funnel()
funel.add(
    " ",
    [list(z) for z in zip(data['Age Group3'], data['Population'])],
    sort_='none',
    label_opts=opts.LabelOpts(position="inside"),
)
funel.set_global_opts(
    title_opts=opts.TitleOpts(
        title="Population Struction of American Year 1990",),
    legend_opts=opts.LegendOpts(
        pos_top='5%', textstyle_opts=opts.TextStyleOpts(font_size=15)),
)
funel.render_notebook()

 从输出结果可以看出：1990 年的美国人口结构以 20-40 的壮年为主。

data = df.loc[df['Year'] == 2019]
data['Age Group3'] = pd.cut(
    data['Mean Age'],
    bins=[0, 20, 40, 70, 100],
    labels=['Youth(<20)', 'Prime(20-40)', 'Middle(40-70)', 'Old(>70)'])
data = data.groupby(['Age Group3'], as_index=False)['Population'].sum()
data['Population'] = data['Population']/np.sum(data['Population'])*100

funel = Funnel()
funel.add(
    " ",
    [list(z) for z in zip(data['Age Group3'], data['Population'])],
    sort_='none',
    label_opts=opts.LabelOpts(position="inside"),
)
funel.set_global_opts(
    title_opts=opts.TitleOpts(
        title="Population Struction of American Year 2019",),
    legend_opts=opts.LegendOpts(
        pos_top='5%', textstyle_opts=opts.TextStyleOpts(font_size=15)),
)
funel.render_notebook()

         从运行结果可以看出，时过境迁，2019 年美国人口结构已悄然下移。

新生儿出生率

        统计各州 <1 和 1-4 两个年龄组（Age Group）的年度人口增长率，分析各州新生儿出生率，数据处理过程详见代码注释。

data = df

# 选出平均年龄小于 3 的样本数据，即对应 <1 和 1-4 两个年龄组
data = data.loc[data['Mean Age'] < 3]

# 空 df 对象，装各州处理后数据
state_data = pd.DataFrame()

for state in list(set(data['State'])):
    # 聚合得到每个州总人数
    tmp = data.loc[data['State'] == state].groupby(
        ['Year'], as_index=False)['Population'].sum()

    # 将 Population 列移位 1 个周期，获得新的特征列 Population Last Year 即 去年总人口数
    tmp['Population Last Year'] = tmp.shift()['Population']

    # 新生儿出生率计算原理为  100*（当年人口数 - 去年人口数） / 去年人口数
    tmp['Birth Increase Ratio /%'] = 100 * (tmp['Population']-tmp['Population Last Year']) / tmp['Population Last Year']

    # 由于 1990 年没有上年数据，因此其增长率计算结果为空值，将其增长率填充为 0
    tmp['Birth Increase Ratio /%'].fillna(value=0, inplace=True)
    tmp['State'] = state

    # 将所有州的数据进行列方向上的合并
    state_data = pd.concat([state_data, tmp])

state_data = state_data.sort_values('Population')

# 查看前 5 行数据
state_data.head()

	Year	Population	Population Last Year	Birth Increase Ratio /%	State
29	2019	29043.0	29625.0	-1.964557	Vermont
28	2018	29625.0	30004.0	-1.263165	Vermont
27	2017	30004.0	30234.0	-0.760733	Vermont
26	2016	30234.0	30539.0	-0.998723	Vermont
25	2015	30539.0	30609.0	-0.228691	Vermont

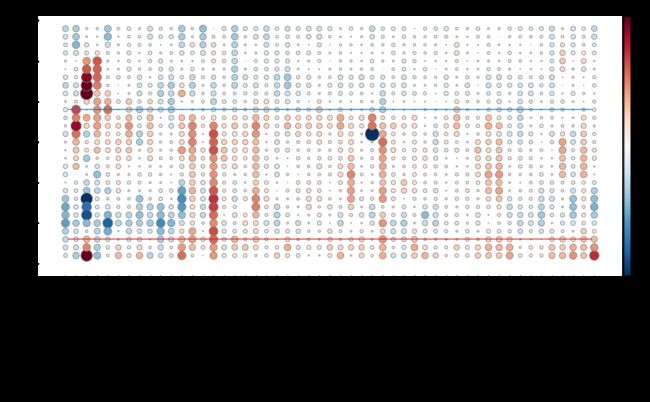
        散点图颜色映射的数据，可通过 plt.colorbar 生成的颜色条做辅助可视化，方便读者阅读每个颜色点对应的绝对数值，其原理是将散点图返回的 mappable 对象传入 plt.colorbar 中，plt.colorbar 生成的颜色条（cbar），其颜色板和显色数据区域通过散点图接口中的 cmap、vmin、vmax等参数控制。

plt.rcParams['figure.figsize'] = (18, 8)

# 生成画布并新增子图，111 表示 1行1列第1个子图
ax = plt.figure().add_subplot(111)

# ax.scatter 接口返回的 mappable 对象，用以传入 plt.colorbar 接口中，实现颜色与数据在颜色条上的映射
mappable = ax.scatter(
    x=state_data['State'],
    y=state_data['Year'],
    c=state_data['Birth Increase Ratio /%'],
    s=np.abs(state_data['Birth Increase Ratio /%'])*50,  # 将增长率为负值的数据取绝对值
    ec='gray',
    vmin=-7,  # 颜色条映射数据最小值
    vmax=7,  # 颜色条映射数据最大值
    cmap=plt.cm.RdBu_r,
)


# 将 x 轴刻度标签旋转 90 度
ax.tick_params(axis='x', rotation=90)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)

# 添加 1993、2009 两条水平辅助线
ax.axhline([1993], xmin=0.05, xmax=0.95, color='tab:red')
ax.axhline([2009], xmin=0.05, xmax=0.95, color='tab:blue')

# 添加颜色条
cbar=plt.colorbar(
    mappable=mappable,
    ax=ax,
    aspect=40,  # 颜色条的长宽比例  =长度/宽度
    pad=0.005,  # 散点图和颜色条的间距
    fraction=0.02  # 散点图和颜色条在画布上宽度的比例  =颜色条宽度/散点图宽度
)

ax.set_title(
    'Birth Increase Ratio of States of American from Year 1990 to 2019')

 从输出结果可以看出：

• 人口基数最大的 California， 1993 年以后新生儿出生率一直处于下降阶段；
• 大多数州在 2009 年以后均呈现出新生儿出生率下降状况；
• North Dakota 和 District of Columbia 两州阶段性地出现婴儿潮。

性别分布

选择 1990 、2010、 2019 三个年份，将数据集按照性别（Gender）、种族（Race）进行人口数（Population）聚合并按升序排列。聚合后，将聚合数据集中的 Gender、Race 特征分别映射至散点图 x、y 坐标，将 Population 人口数特征映射至点大小（s），将 Gender 映射至点颜色（c）。

fig, axs = plt.subplots(1, 3, figsize=(15, 6), sharey=True, sharex=True)

for i, year in enumerate([1990, 2010, 2019]):
    ax = axs[i]
    data = df.loc[df['Year'] == year].groupby(
        ['Gender', 'Race'], as_index=False)['Population'].sum().sort_values('Population')
    data

    ax.scatter(
        x=data['Gender'],
        y=data['Race'],
        c=data['Gender'].apply(lambda x: 'tab:red' if x ==
                               'Female' else 'tab:blue'),
        s=data['Population']*0.00007,
        ec='gray',
    )

    ax.set_ylim(-0.5, 4)
    ax.set_xlim(-1, 1.5)
    ax.set_title('Year %d' % year)

    if i > 0:
        ax.spines['left'].set_visible(False)

fig.suptitle('Population Distribution Varies with Gender of USA',
             size=25, va='bottom')

         从输出结果可以看出，各种族在选定的3个年份并未呈现出显著差异，说明美国的人口结构中，性别分布相对均匀。

实验总结

本实验以散点图为主要绘图对象，对美国 1990 - 2019 年期间人口与种族变迁做了研究，通过分析和可视化，得出以下结论：

• 美国是以白人为主体种族的国家，在各大州白人的数量和占比都具有绝对优势；
• 在过去的 29 年间，白人一直保持着与美国国家人口增速相同的增长速率；
• 黑人和亚裔作为仅次于白人排名的种族，在过去 29 年间有了较高的增速，且主要人口增速表现出一定的地域性；
• 美国在人口结构上，正逐渐趋向于老龄化，与此同时，新生儿出生率自 2009 年以后有了较为明显的下降；
• 各种族在统计期内性别比例未出现较明显的失衡。

本次实验中，我们学会了：

• 散点图接口及其参数的使用。
• 漏斗图的绘制。
• 画布上多子图的绘制。
• 散点图的数据拟合。
• 颜色条的绘制和应用。
• 数据对数变换技巧。