五大常规算法

分治法
见名思义，即分而治之，从而得到我们想要的最终结果。分治法的思想是将一个规模为 N 的问题分解为 k 个较 小的子问题，这些子问题遵循的处理方式就是互相独立且与原问题相同。
两部分:
分（divide）：递归解决较小的问题 ;
治（conquer）：然后从子问题的解构建原问题的解;
三个步骤
1、分解（Divide）：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
2、解决（Conquer）：若子问题规模较小而容易被解决则直接解决，否则递归地解各个子问题；
3、合并（Combine）：将各个子问题的解合并为原问题的解;

实现代码

#include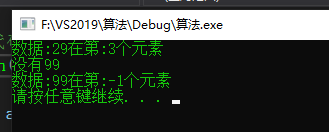 
//分治法
int divide(int *array, int minSub, int maxSub, int number) {
	if (minSub > maxSub) {
		printf("没有%d\n", number);
		return -1;//没有nuber这个值的时候返回-1
	}
	//取中间位置的值
	int index =(int)( (minSub + maxSub) / 2);

	if (number==array[index]) {
		return index;
	}
	else if (number<array[index]) {
		return divide(array, minSub, index-1, number);
	}
	else {
		return divide(array,index+1,maxSub,number);
	}
}
//测试代码
int main(void) {

	int arr[] = { 2,10,15,29,30,77 };

	printf("数据:%d在第:%d个元素\n", 29, divide(arr, 0, sizeof(arr)/sizeof(arr[0]),29));
	printf("数据:%d在第:%d个元素\n",99, divide(arr,0, sizeof(arr)/sizeof(arr[0]),99));

	system("pause");
	return 0;
}

动态规划法
从上往下分析问题，大问题可以分解为子问题，子问题中还有更小的子问题 比如总共有 5 级台阶,求有多少种走法；由于机器人一次可以走两级台阶，也可以走一级台阶，所以我们可以分成两个情况:

1. 机器人最后一次走了两级台阶，问题变成了“走上一个 3 级台阶，有多少种走法？”
2. 机器人最后一步走了一级台阶，问题变成了“走一个 4 级台阶，有多少种走法？”
3. 边界情况分析 走一步台阶时，只有一种走法，所以 f(1)=1 走两步台阶时，有两种走法，直接走 2 个台阶，分两次每次走 1 个台阶，所以 f(2)=2 走两个台阶以上可以分解成上面的情况;
   代码实现:

#include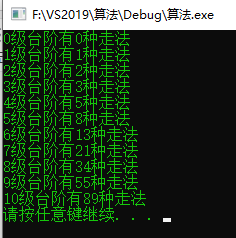 

//动态规划法
//递归实现机器人台阶走法统计参数:
//n 个台阶,返回上台阶总的走法
int daynamic(int n) {
	if (n <= 0) {
		return 0;
	}
	if (n == 1) {
		return 1;
	}
	if (n == 2) {
		return 2;
	}

	//分配一块动态内存保存结果
	int* val = new int[n+1];
	val[0] = 0;
	val[1] = 1;
	val[2] = 2;

	for (int i = 3; i <= n; i++) {
		val[i] = val[i - 1] + val[i - 2];
	}

	int ret = val[n];
	delete[] val;

	return ret;
}
//测试代码
int main(void) {
	printf("%d级台阶有%d种走法\n", 10, daynamic(10));
	system("pause");
	return 0;
/*	动态规划也是一种分治思想，但与分治算法不同的是，分治算法是把原问题分解为若干子问题， 自顶向下，求解各子问题，合并子问题的解从而得到原问题的解。动态规划也是自顶向下把原问 题分解为若干子问题，不同的是，然后自底向上，先求解最小的子问题，把结果存储在表格中， 在求解大的子问题时，直接从表格中查询小的子问题的解，避免重复计算，从而提高算法效率。*/
}

回溯法
在问题的解空间中，按深度优先遍历策略，从根节点出发搜索解空间树。算法搜索至解空间 的任意一个节点时，先判断该节点是否包含问题的解。如果确定不包含，跳过对以该节点为根的 子树的搜索，逐层向其祖先节点回溯，否则进入该子树，继续深度优先搜索。 回溯法解问题的所有解时，必须回溯到根节点，且根节点的所有子树都被搜索后才结束。回 溯法解问题的一个解时，只要搜索到问题的一个解就可结束。
回溯的基本步骤 :

1. 定义问题的解空间
2. 确定易于搜索的解空间结构
3. 以深度优先搜索的策略搜索解空间，并在搜索过程中尽可能避免无效搜索

#include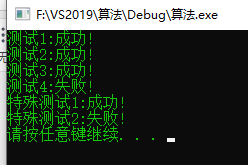 

/*实现一个回溯函数实现查找矩阵中是否含有str指定的字符串
  参数说明:
			matrix  输入矩阵
			rows    矩阵行数
			cols    矩阵列数
			str		需要搜索的字符串
			返回值: 是否找到 是(true), 否(false)   */

//探测下一个字符是否存在
bool hasPathCore(const char* matrix, int rows, int cols, int row, int col, const char* str, int& pathLength, bool *visited) {
	if (str[pathLength] == '\0') {
		return true;
	}

	bool hasPath = false;
	if (row >= 0 && row < rows && col >= 0 && col < cols && matrix[row * cols + col] == str[pathLength] && !visited[row * cols + col]) {

		pathLength++;
		visited[row * cols + col] = true;

		hasPath = hasPathCore(matrix, rows, cols, row, col - 1, str, pathLength, visited)
			|| hasPathCore(matrix, rows, cols, row - 1, col, str, pathLength, visited)
			|| hasPathCore(matrix, rows, cols, row, col + 1, str, pathLength, visited)
			|| hasPathCore(matrix, rows, cols, row + 1, col, str, pathLength, visited);

		if (!hasPath) {
			pathLength--;
			visited[row * cols + col] = false;
		}
	}

	return hasPath;
}

bool hasPath(const char* matrix, int rows, int cols, const char* str) {
	if (matrix == NULL || rows < 1 || cols < 1 || str == NULL) {
		return false;
	}
	
	bool* visited = new bool[rows * cols];
	memset(visited, 0, rows * cols);
	
	int pathLength = 0;
	//遍历矩阵中每个点,作为起点开始进行搜索
	for (int row = 0; row < rows; row++) {
		for (int col = 0; col < cols; col++) {

			if (hasPathCore(matrix, rows, cols, row, col, str, pathLength, visited)) {
				return true;
			}
		}
	}
	delete[] visited;

	return false;
}

//单元测试代码
void test(const char* testName, const char* matrix, int rows, int cols, const char* str, bool expected) {
	if (testName != NULL) {
		printf("测试的函数名:%s", testName);
	}
	
	if (hasPath(matrix, rows, cols, str) == expected) {
		printf("成功!\n");
	}
	else {
		printf("失败!\n");
	}
}

void test1() {
	/*ABCD
	  EFGH
	  IJKL*/

	const char* matrix = "ABCDEFGHIJKL";
	const char* str = "ABCD";
	test("测试1:",(const char*)matrix, 3, 4, str, true);

	const char* str1 = "AEIJ";
	test("测试2:", (const char*)matrix, 3, 4, str1, true);

	const char* str2 = "ABFG";
	test("测试3:", (const char*)matrix, 3, 4, str2, true);

	const char* str3 = "ABGK";
	test("测试4:", (const char*)matrix, 3, 4, str3, true);

	const char* matrix_T = "A";
	const char* str_T = "A";
	test("特殊测试1:", (const char*)matrix_T, 1, 1, str_T, true);

	const char* str_T1 = "B";
	test("特殊测试2:", (const char*)matrix_T, 1, 1, str_T1, true);
}

//测试代码
int main(void) {

	test1();

	system("pause");
	return 0;
}

贪心算法
贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有 利)的选择，从而希望能够导致结果是最好或者最优的算法;
贪婪算法所得到的结果往往不是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最 优解的结果。
贪婪算法并没有固定的算法解决框架，算法的关键是贪婪策略的选择，根据不同的问题选择 不同的策略;
基本的解题思路为：

1. 建立数学模型来描述问题
2. 把求解的问题分成若干个子问题  对每一子问题求解，得到子问题的局部最优解
3. 把子问题对应的局部最优解合成原来整个问题的一个近似最优解

#include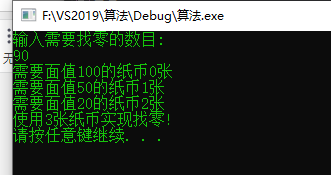 

#define MAX 6

/*对输入的零钱数,找到至少要用的钱币的数量
  参数:
	   money  也找或者支付的零钱数
  返回:
	   至少要用的钱币的数量,-1表示找不开 */

int val[MAX] = { 1,5,10,20,50,100 };//钱的面值
int count[MAX] = { 10,2,3,2,1,1 };//每个面值的数量

int solve(int money) {

	int num = 0;
	for (int i = MAX - 1; i >= 0; i--) {
		
		int k = money / val[i];//如:找120,就给一张100,一张20
		int n = k > count[i] ? count[i] : k;

		printf("需要面值%d的纸币%d张\n", val[i], n);

		money -= n * val[i];
		num += n;

		if (money == 0) {
			break;
		}
	}

	if (money > 0) {
		num = -1;
	}

	return num;
}

//测试代码
int main(void) {

	int money = 0;
	int num = 0;

	printf("输入需要找零的数目:\n");
	scanf_s("%d", &money);

	num = solve(money);

	if (num == -1) {
		printf("没有这么多零钱!");
	}
	else {
		printf("使用%d张纸币实现找零!\n", num);
	}

	system("pause");
	return 0;
}

分支定界法
分支定界 (branch and bound) 算法是一种在问题的解空间上搜索问题的解的方法。但与回溯算 法不同，分支定界算法采用广度优先或最小耗费优先的方法搜索解空间树，并且，在分支定界算 法中，每一个活结点只有一次机会成为扩展结点。
利用分支定界算法对问题的解空间树进行搜索，它的搜索策略是：
1 ．产生当前扩展结点的所有孩子结点；
2 ．在产生的孩子结点中，抛弃那些不可能产生可行解（或最优解）的结点；
3 ．将其余的孩子结点加入活结点表；
4 ．从活结点表中选择下一个活结点作为新的扩展结点。 如此循环，直到找到问题的可行解（最优解）或活结点表为空。 从活结点表中选择下一个活结点作为新的扩展结点，根据选择方式的不同，
分支定界算法通 常可以分为两种形式：
1 ． FIFO(First In First Out)(先进先出) 分支定界算法：按照先进先出原则选择下一个活结点作为扩展结 点，即从活结点表中取出结点的顺序与加入结点的顺序相同。
2 ．最小耗费或最大收益分支定界算法：在这种情况下，每个结点都有一个耗费或收益。假 如要查找一个具有最小耗费的解，那么要选择的下一个扩展结点就是活结点表中具有最小 耗费的活结点；假如要查找一个具有最大收益的解，那么要选择的下一个扩展结点就是活 结点表中具有最大收益的活结点;
(代码可以参考A*算法)