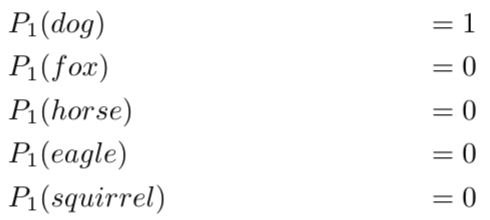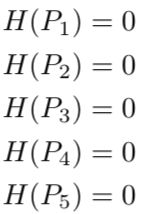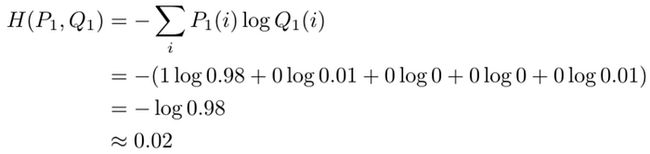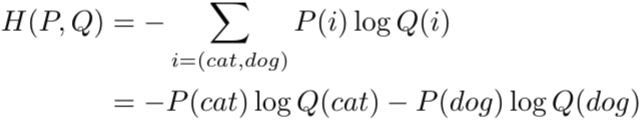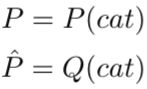一文懂交叉熵Cross-Entropy

        本文翻译自https://naokishibuya.medium.com/demystifying-cross-entropy-e80e3ad54a8

        交叉熵由交叉（Cross）和熵（Entropy）两部分组成，在机器学习中常常被定义为损失函数的目标。在二分类任务中，更有二分类交叉熵作为训练目标函数。

一、熵的表达式

        在前文一文懂熵Entropy_liveshow021_jxb的博客-CSDN博客中，指出熵的数学表达式为

        上述表达式是离散的变量i。对于连续变量，可以写成积分的形式

 

        上式中，x表示连续变量，P(x)表示概率密度函数。

        在上面两者计算表达式中，都是负对数概率的期望平均值。所以，也可以用期望来表示

        x~P表示离散或者连续变量x用概率分布P来计算期望。记H(P)为熵，则最终可以表示为

        简言之，熵表示遵循特定概率分布事件的理论最小平均编码长度。

        可以看出，知道概率分布，就能计算熵。反之，不知道概率分布，则不能计算熵。为了求熵，就需要先估计概率分布。这种情况下，熵也是估计熵了。

二、估计熵

        回到前文一文懂熵Entropy_liveshow021_jxb的博客-CSDN博客中的例子，向纽约发送东京的天气，并且希望将消息编码为尽可能短的长度。在真实事件发生前，是没办法知道各种天气的发生概率的。假设，经过一段时间的观察，将东京天气的概率分布估计为Q，此时估计的熵为

        如果估计的概率分布Q接近真实的概率分布，则上式能给出最小编码长度，即真实的熵。但是估计的概率分布很可能与真实的概率分布差的很远。此时既影响了期望，也影响了编辑长度的计算。最后的估计熵与真实熵就差的很远了。

        为了让编码长度尽可能的小，用真实概率分布P和基于估计概率Q的编码大小来计算平均编码长度。这种计算方式就称为P和Q之间的交叉熵。

        所以，交叉熵比较了实际使用的编码大小和理论最小编码，即交叉验证编码大小。

三、交叉熵>=熵

        记H(P,Q)为交叉熵，则最终可以表示为

     

        注意上式中的P和Q位置不能互换，因为是用真实概率分布算期望，估计概率分布算编码大小。

        如果估计概率分布Q是精确的，即Q=P，此时

        估计概率分布Q是非精确时，

四、交叉熵作为损失函数

        现在有一个动物图像的数据集，里面有5种不同的动物，每张图片中都只有一个动物。

Source: https://www.freeimages.com/

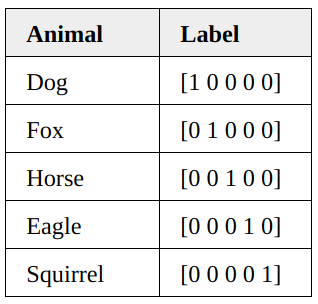
        每张图片用one-hot编码到相应的动物，如下所示

        这种one-hot编码也可以看成每张图片在5种动物上的概率分布。比如第一张图片在“狗”这个种类上的概率为1，在其他种类上的概率为0。

        每张图片的分类都知道了，此时的熵都是0。

        one-hot编码能100%的表明每张图片中是什么动物种类。不会说第一张图片90%是狗，10%是猫。现在有一个机器学习模型要对这些图片进行分类。当这个模型没有被充分训练时，可能会将第一张图片分类如下

        模型将这张图片40%判定为狗，30%判定为狐狸，5%判定为马，5%判定为鹰，20%判定为松鼠。这种估计对于第一张图片上的动物是什么种类没有给出高置信度。那么在这种估计下的交叉熵为

        这远远大于标签下的熵为0的情况。假设模型进行了改良，此时对第一张图片的分类概率如下

        此时，交叉熵为

        可以看到，交叉熵随着分类准确性的提升，会变小。当分类100%准确时，交叉熵也会等于0。所以，交叉熵是可以作为损失函数来训练分类模型的。

五、二分类的交叉熵

        当遇到二分类问题时，就可以用二分类的交叉熵作为损失函数了。例如上面的例子中，假设图片上的动物只有两类：猫和狗。此时，交叉熵表示如下：

        使用如下等式做进一步替换

        则

        令如下关系

        此时，二分类交叉熵就可以表示为

        这个表达式就是在各种文献中常常看到的了。

六、2为底还是自然数e为底

        在机器学习中，常常使用自然数e为底，来替代使用2为底，这样便于计算导数。因为

        对数底的变化不会引起任何问题，因为这只是改变了个常数。

        例如，使用交叉熵作为分类的损失函数仍然是成立的，因为训练时只需要往目标越来越小的方向迭代就可以。

        作为概念，以自然数e为底的信息单位是奈特nat，以2为底的信息单位是比特bit。1nat中的信息量为按1/e概率发生的事件。

        1bit的信息量来自发生概率为1/2的事件。当把信息编码为1bit时，一条信息能减少50%的不确定性。比如收到新来报道的同学是男同学（假设男女的概率各为1/2），则从全部人口中减少了一半人，只需要从剩下的一半人中确认是哪个同学了。但以e为对数底时，不太好解释。

        综合上述，以2为对数底用来解释信息熵的概念，以e为对数底用来做数值计算。

        自此，把交叉熵彻底理解清楚了。交叉熵这个概念对你的熵就是0了。

参考

https://naokishibuya.medium.com/demystifying-cross-entropy-e80e3ad54a8

https://zhuanlan.zhihu.com/p/149186719