每日刷题总结——双指针
目录
- 双指针
-
- 202. 快乐数
- 1229. 安排会议日程
- 287. 寻找重复数
- ⭐42. 接雨水【难】
- 1868. 两个行程编码数组的积
双指针
202. 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/happy-number
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
通过例子我们会发现,如果之前出现的数字之后计算又出现了,说明肯定不是快乐数
例如:2——>4——>16——>37——>58——>89——>145——>42——>20——>4
⬆_____________________________________________________⬇
我们发现什么?变环了! 解决环形问题应该怎么做?大声告诉我!双指针!!!!
具体思路:
- 定义快慢指针,让他们一直循环计算,肯定有一天快指针会等于慢指针。
- 只要快指针等于慢指针我就退出循环
- 然后看他们的值,如果等于1,就是快乐数,不是1就不是快乐数
代码实现
public boolean isHappy(int n) {
int fast=n;
int slow=n;
do{
slow=squareSum(slow);
fast=squareSum(fast);
fast=squareSum(fast);
}while(slow!=fast);
if(fast==1)
return true;
else return false;
}
private int squareSum(int m){
int squaresum=0;
while(m!=0){
squaresum+=(m%10)*(m%10);
m/=10;
}
return squaresum;
}
1229. 安排会议日程
给定两个人的空闲时间表:slots1 和 slots2,以及会议的预计持续时间 duration,请你为他们安排 时间段最早 且合适的会议时间。
如果没有满足要求的会议时间,就请返回一个 空数组。
「空闲时间」的格式是 [start, end],由开始时间 start 和结束时间 end 组成,表示从 start 开始,到 end 结束。
题目保证数据有效:同一个人的空闲时间不会出现交叠的情况,也就是说,对于同一个人的两个空闲时间 [start1, end1] 和 [start2, end2],要么 start1 > end2,要么 start2 > end1。
示例 1:
输入:slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 8
输出:[60,68]
示例 2:
输入:slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 12
输出:[]
思路:
- 双指针思路,一个遍历slots1,一个遍历slots2
- 从前往后遍历,只要slots1和slots2最早的结束时间减去slots1和slots2最晚的开始时间的差能满足条件则直接返回即可(如此一来也满足了最早时间段这个条件)
ps:注意要先排序
代码实现:
class Solution {
public List<Integer> minAvailableDuration(int[][] slots1, int[][] slots2, int duration) {
Arrays.sort(slots1, (o1, o2) -> o1[0] - o2[0]);//排序
Arrays.sort(slots2, (o1, o2) -> o1[0] - o2[0]);//排序
List<Integer> res = new ArrayList<>();
int s1 = slots1.length;
int s2 = slots2.length;
int start1 = 0;//指针1
int start2 = 0;//指针2
while (start1 < s1 && start2 < s2) {//结束条件
int start = Math.max(slots2[start2][0], slots1[start1][0]);
int cha = Math.min(slots2[start2][1], slots1[start1][1]) - start;//计算交集时间
if (cha >= duration) {//看是否满足条件
res.add(start);
res.add(start + duration);
//找到就退出,这样就满足了时间段最早这个条件
break;
} else {//不满足条件
if (slots1[start1][1] < slots2[start2][1]) {//如果是第一个人的时间没赶上第二个人的时间
start1++;
continue;
} else if (slots2[start2][1] < slots1[start1][1]) {//如果是第二个人的时间没赶上第一个人的时间
start2++;
continue;
} else {
start1++;
start2++;
}
}
}
return res;
}
}
287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
思路:
实际上这个跟快乐数是一样的,快慢针就行了。
- 快慢指针思想, fast 和 slow 是指针, nums[slow] 表示取指针对应的元素
注意 nums 数组中的数字都是在 1 到 n 之间的(在数组中进行游走不会越界),
因为有重复数字的出现, 所以这个游走必然是成环的, 环的入口就是重复的元素,
即按照寻找链表环入口的思路来做
代码实现:
class Solution {
public int findDuplicate(int[] nums) {
int fast = 0, slow = 0;
while(true) {
fast = nums[nums[fast]];
slow = nums[slow];
if(slow == fast) {
fast = 0;
while(nums[slow] != nums[fast]) {
fast = nums[fast];
slow = nums[slow];
}
return nums[slow];
}
}
}
}
⭐42. 接雨水【难】
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
思路:
起先思路就是我左边找个最大的,右边找个最大的,然后我计算当前这个位置存储的雨水量,如此一来就能求出总的雨水量了。但是这个思路的复杂度很高。因为我从左往右遍历的同时还要左右分别遍历求取最高值,时间复杂度为O(n²)。
- 为了更简洁,我们采用向左向右看齐的思想。也就是我往左看,我能看到的最高的值,我就把他当作我能获取的最高的水的高度。我向右看,我把能看到的最高值当作我能获取的最高的水的高度
- 我们在从前往后遍历,取雨水相对低的那个即可。然后累加就是结果。不懂?看图↓
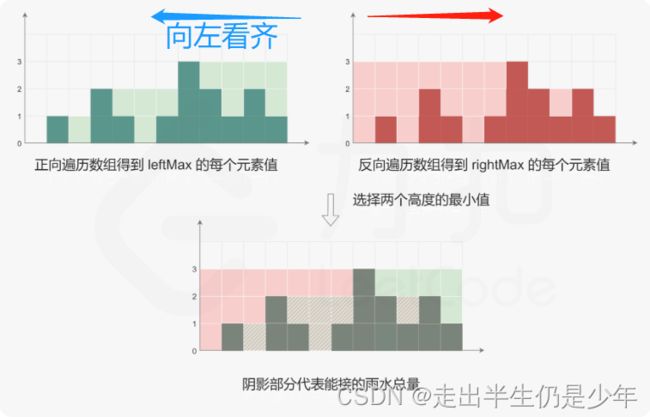
代码实现
class Solution {
public int trap(int[] height) {
int len = height.length;
if (len == 0) {
return 0;
}
int[] leftMax = new int[len];
leftMax[0] = height[0];
for (int i = 1; i < len; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
int[] rightMax = new int[len];
rightMax[len - 1] = height[len - 1];
for (int i = len - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < len; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
}
1868. 两个行程编码数组的积
行程编码(Run-length encoding)是一种压缩算法,能让一个含有许多段连续重复数字的整数类型数组 nums 以一个(通常更小的)二维数组 encoded 表示。每个 encoded[i] = [vali, freqi] 表示 nums 中第 i 段重复数字,其中 vali 是该段重复数字,重复了 freqi 次。
例如, nums = [1,1,1,2,2,2,2,2] 可表示称行程编码数组 encoded = [[1,3],[2,5]] 。对此数组的另一种读法是“三个 1 ,后面有五个 2 ”。
两个行程编码数组 encoded1 和 encoded2 的积可以按下列步骤计算:
将 encoded1 和 encoded2 分别扩展成完整数组 nums1 和 nums2 。
创建一个新的数组 prodNums ,长度为 nums1.length 并设 prodNums[i] = nums1[i] * nums2[i] 。
将 prodNums 压缩成一个行程编码数组并返回之。
给定两个行程编码数组 encoded1 和 encoded2 ,分别表示完整数组 nums1 和 nums2 。nums1 和 nums2 的长度相同。 每一个 encoded1[i] = [vali, freqi] 表示 nums1 中的第 i 段,每一个 encoded2[j] = [valj, freqj] 表示 nums2 中的第 j 段。
返回 encoded1 和 encoded2 的乘积。
注:行程编码数组需压缩成可能的最小长度。
示例 1:
输入: encoded1 = [[1,3],[2,3]], encoded2 = [[6,3],[3,3]]
输出: [[6,6]]
解释n: encoded1 扩展为 [1,1,1,2,2,2] ,encoded2 扩展为 [6,6,6,3,3,3]。
prodNums = [6,6,6,6,6,6],压缩成行程编码数组 [[6,6]]。
示例 2:
输入: encoded1 = [[1,3],[2,1],[3,2]], encoded2 = [[2,3],[3,3]]
输出: [[2,3],[6,1],[9,2]]
解释: encoded1 扩展为 [1,1,1,2,3,3] ,encoded2 扩展为 [2,2,2,3,3,3]。
prodNums = [2,2,2,6,9,9],压缩成行程编码数组 [[2,3],[6,1],[9,2]]。
思路:
这题还是挺简单的,双指针遍历呗,一个遍历encoded1,一个遍历encoded2。遍历的同时将结果add进res中。
细节:
- encoded1和encoded2总归有一个是比较小的,那么我们将encoded值完全取出的那个二维数组就可以i++取下一个了,而还剩了一些encoded 的值的那个二维数组仅仅需要更改当前值的个数。
- 如果我当前这一轮计算的值跟前面一轮计算的值相等,那我不用往res里添加了,仅仅将前一轮出现的次数加上这一轮的次数即可。
代码实现:
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> findRLEArray(int[][] encoded1, int[][] encoded2) {
int i = 0, j = 0;
int len1 = encoded1.length, len2 = encoded2.length;
int rem1 = encoded1[0][1], rem2 = encoded2[0][1];//初始化
while (i < len1 && j < len2) {
int multi1 = encoded1[i][0];
int multi2 = encoded2[j][0];
int min = Math.min(rem1, rem2);
toResult(multi1 * multi2, min);//乘积和
//-------肯定有一个是0---------//
rem1 -= min;
rem2 -= min;
//为0的那个下移,不为0的那个保持原状,但是freq得去掉已经计算过的
if (rem1 == 0) {
i++;
if (i < len1) {
rem1 = encoded1[i][1];//下移
}
}
if (rem2 == 0) {
j++;
if (j < len2) {
rem2 = encoded2[j][1];
}
}
}
return res;
}
private void toResult(int num, int freq) {
if (res.isEmpty()) {//如果是空的
res.add(Arrays.asList(num, freq));//直接添加
} else {//如果不是空的
List<Integer> list = res.get(res.size() - 1);//取出最后一个值,
if (list.get(0) == num) {//跟最后一个相等,那就继续往上加
list.set(1, list.get(1) + freq);
} else {
res.add(Arrays.asList(num, freq));//否则加载末尾
}
}
}
}
