第一章:part2多输入的回归模型
为了使回归模型变得更快并且可以添加更多特征
多维特征
我们可以使输入量具有多个特征:
例如:大小(x1)、房间数量(x2)、楼层(x3)、年限(x4)
- 特殊符号
n:表示一共有几个特征
x j : 表示第几个特征值(列) x_j:\text{表示第几个特征值(列)} xj:表示第几个特征值(列)
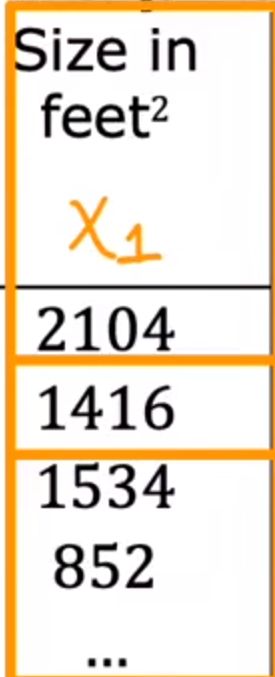
x ⃗ ( i ) : 表示第几个训练样本(行) \vec{x}^{(i)}:\text{表示第几个训练样本(行)} x(i):表示第几个训练样本(行)
例:x^2
所以,现在的多维函数可以写成:
f w , b ( x ) = w 1 x 1 + w 2 x 2 + . . . + w n x n + b = w ⃗ ⋅ x ⃗ + b f_{w,b}(x)=w_1x_1+w_2x_2+...+w_nx_n+b=\vec{w} \cdot\vec{x}+b fw,b(x)=w1x1+w2x2+...+wnxn+b=w⋅x+b
向量化
将上述方法进行向量化可以大大提升代码效率(因为一些库会直接调用GPU进行运算)
可以下面的参数使用矩阵表示:

# 表示参数
w = np.array([1.0,2.5,-3.3])
b = 4
x = np.array([10,20,30])
# 表示f(x)
#f =w[0] * x[0] + w[1] * x[1] + w[2] * x[2] + b//麻烦,且不高效
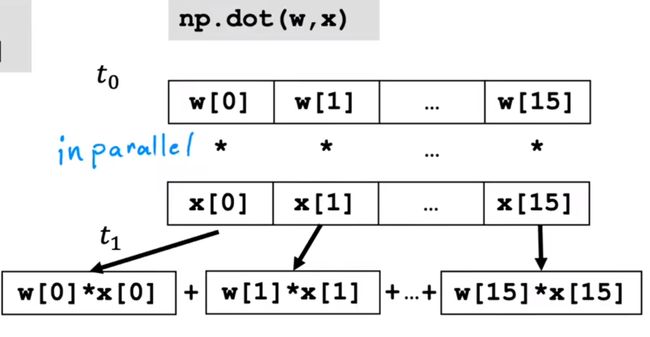
f = np.dot(w,x) + b
运行理论:
两个方法如果在数据集很大时第二种方法更具有优势性
传统方法:一遍遍遍历

向量化方法:并行运行
向量化与多元梯度下降算法
根据上述向量化算法,我们可以将多元损失函数写为:
J ( w 1 , w 2 . . . , w n , b ) = J ( w ⃗ , b ) J(w_1,w_2...,w_n,b)=J(\vec{w},b) J(w1,w2...,wn,b)=J(w,b)
所以多元梯度下降也可以表示为:
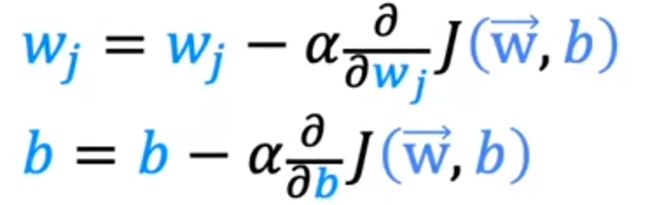
将损失函数表达式(1)代入上述式子
J ( w , b ) = 1 2 m ∑ i = 0 m ( f w , b ( x ( i ) ) − y ) 2 (1) J(w,b)=\frac{1}{2m}\sum_{i=0}^{m} (f_{w,b}(x^{(i)})-y)^2\tag{1} J(w,b)=2m1i=0∑m(fw,b(x(i))−y)2(1)
最终可以得到不同的w与一个b:
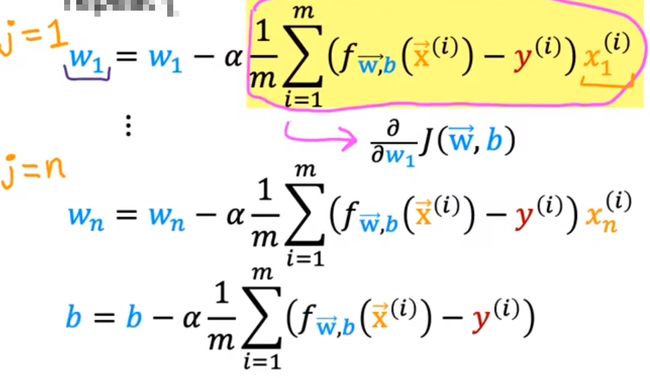
现在我们知道了如何求解多元斜率(w)与b,下面我们将了解选择良好的特征缩放(x)与学习率(α)
特征缩放
介绍特征缩放
在面对一些数据特征时,他们的大小可能相差很大:
x 1 ( 房间大小 ) = 200 , x 2 ( 房间数目 ) = 5 x_1(房间大小)=200,x_2(房间数目)=5 x1(房间大小)=200,x2(房间数目)=5
我们应该取合适的w值,使得回归方程预测合理:
w1应该小一些,w2应该大一些
p r i c e ^ = w 1 ∗ x 1 + w 2 ∗ x 2 + b \widehat{price}=w_1*x_1+w_2*x_2+b price =w1∗x1+w2∗x2+b
这种方式不利于分析与计算,并且会导致运算梯度下降法速度下降
所以我们应该统一放缩x1与x2(例如都放缩到0-1)

这样梯度下降算法可以计算更加快速(等高线图):
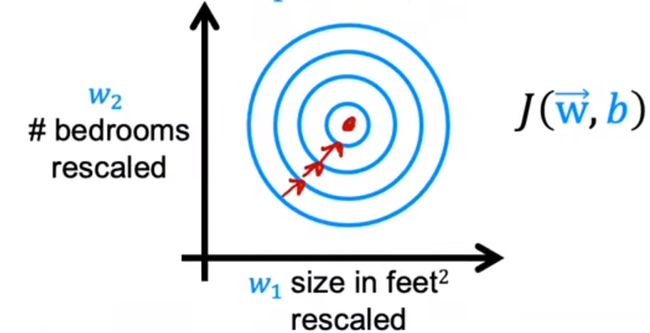
实现特征缩放
假设:
300 ≤ x 1 ≤ 2000 300\leq x1\leq2000 300≤x1≤2000
0 ≤ x 2 ≤ 5 0\leq x2\leq5 0≤x2≤5
-
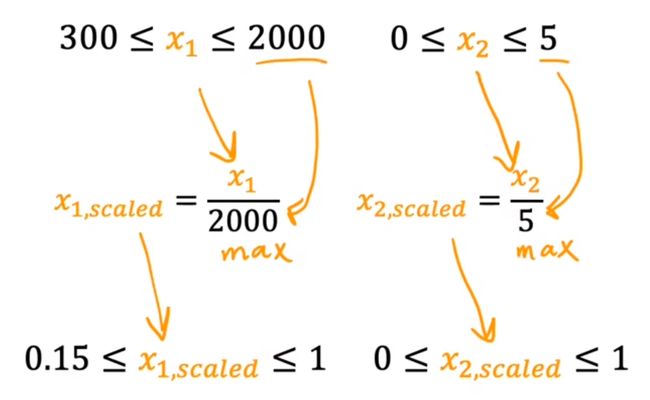
方法1:除以最大值
将放缩后的范围调整成0-1
数据图:
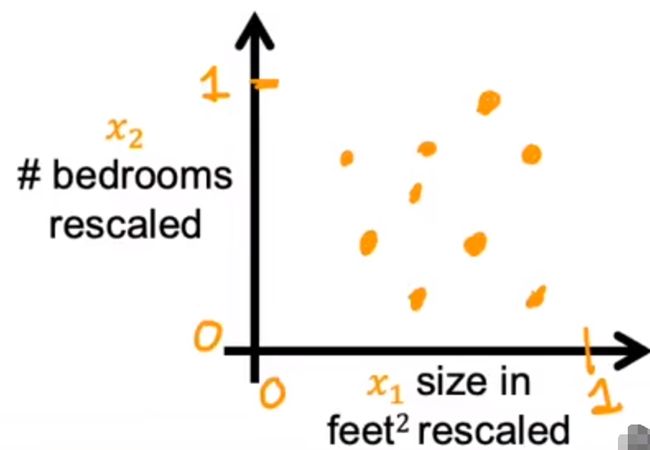
-
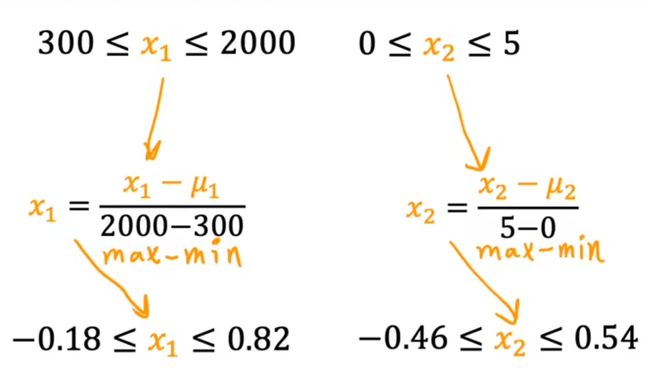
方法2:平均值标准化
将放缩后的范围调整成-1 - 1
μ:平均值
数据图:
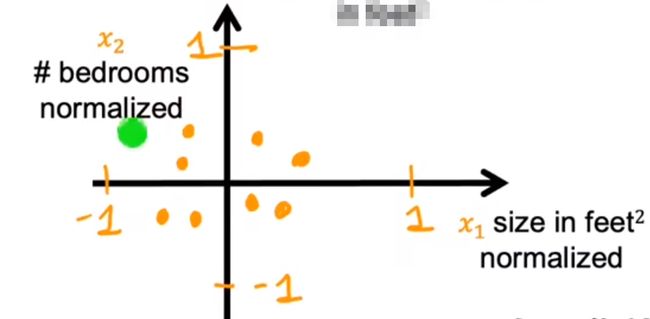
-
方法3:Z-score 标准化
计算标准差(σ),均值(μ)
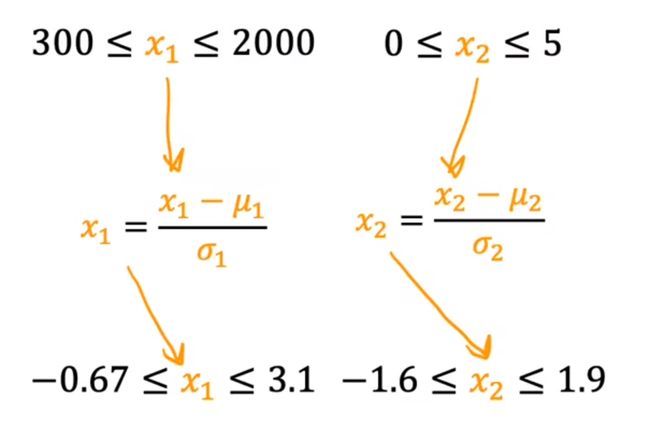
数据图:

判断梯度下降是否收敛
可以判断代价函数是否下降
横轴:迭代次数,纵轴:代价函数大小

如果代价函数J(w,b)异常上升:
- 学习率(α)选择不好
- 代码有问题
另外,在最后的曲线趋于平缓的时候:说明梯度下降已经完成
-
判断梯度下降已经完成方法
第一种方法较好:因为自动收敛的数值不好确定
-
通过观察上述绘图进行估计(较优)
-
自动收敛测试
-
ϵ :表示一个小数字的变量 \epsilon:表示一个小数字的变量 ϵ:表示一个小数字的变量
当代价函数J(w,b)的减小值<ε,则可以表明其收敛
如何设置学习率
如果学习率(α)过小:算法运行次数会很大,慢
如果学习率(α)过大:可能不会收敛
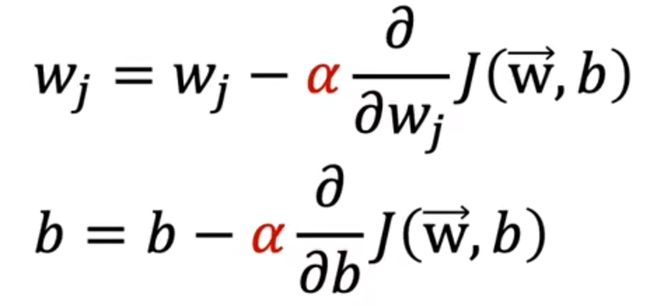
-
设置学习率的方法
首先尝试不同的学习率:
将他们的图像画出并观察

观察图表后选择一个合适的学习率
特征工程
为预测数据选择合适的特征值进行训练,是十分重要的
例:
构建预测一个房子的回归方程:

- 如果只使用宽度与深度(表示房间分别与宽度与深度的关系)
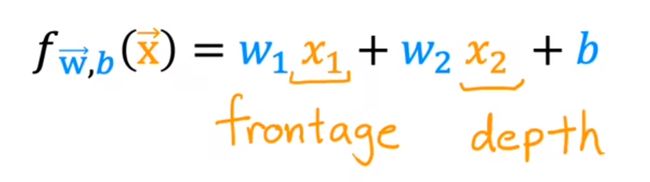
但在实际中,可能房价与实际的土地面积有关(x1*x2)
- 构建面积(x3)作为第三特征值
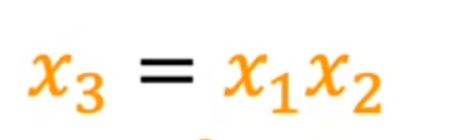
这一种构建结果可能比上述更加准确
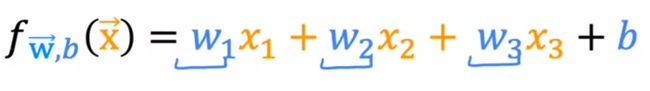
多项式回归模型
如果一个数据集无法使用直线进行拟合,
我们结合多元线性回归与特征工程,生成了多项式回归模型
例:直线拟合不好的数据

我们可以使用二次函数:
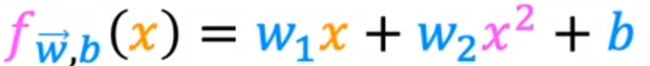
但是二次函数最终会下降,放在价格上不合理

我们可以使用三次函数:

这样随着大小上升价格不会下降
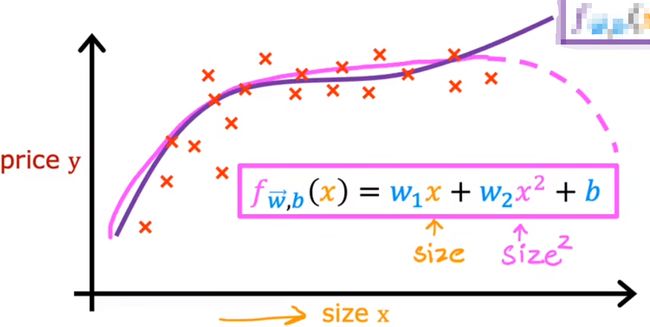
以上就是拟合曲线的几种方法,关于如何选择使用哪种方法去拟合,这会在第二部分:高级学习算法 中讲到
使用sklearn可以快速构建模型
