C 非线性结构——树 万字详解(通俗易懂)
目录
一、树的介绍
1.定义 :
2.相关概念 :
3.简单分类 :
4.相关应用 :
二、树的存储
1.二叉树的存储 :
1° 二叉树连续存储
2° 二叉树链式存储(常用)
2.普通树和森林的存储 :
1° 普通树的存储
2° 森林的存储
三、树的遍历
1.二叉树先序遍历 :
2.二叉树中序遍历 :
3.二叉树后序遍历 :
四、树的还原
1.概述
2.已知先序和中序求后序 :
3.已知中序和后序求原始二叉树 :
五、树的程序演示
1.静态创建与遍历
2.动态创建与遍历
一、树的介绍
1.定义 :
没有父结点的结点称为根结点,一棵树中有且只有一个称为“根”的结点;并且有若干个互不相交的子树,这些子树本身也是一棵树。
每个结点都只有有限个子结点或无子结点;每一个非根结点都有且只有一个父结点。
2.相关概念 :
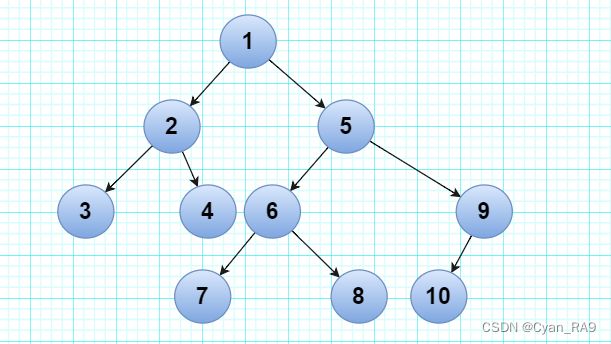
1° 父结点和子结点——针对于两个结点的关系,被指向的结点称为子结点,指向该结点的结点称为父结点。如下图所示 :
2° 深度——令根结点为树的第一层,从根结点开始到最底层结点的层数称为树的深度。如下图所示 :
3° 叶子结点和非叶子结点——叶子结点指没有子结点的结点;非叶子结点指有子结点的结点,非叶子结点也叫非终端结点。如下图所示 :
4° 度——某一个结点的子结点的个数,称为该结点的度;对应地,取一棵树中度最大的结点的度,称为这棵树的度。如下图所示 :
3.简单分类 :
1° 一般树——任意一个结点的子结点的个数都不受限制。如下图所示 :
2° 二叉树——任意一个结点的子结点的个数最多有2个,且子结点的位置不可更改(即左子树和右子树),所以二叉树都是有序树。
Δ二叉树又可再分类 :
①一般二叉树
②满二叉树——在不增加树的层数的前提下,无法再向树中再多添加一个结点的二叉树,称为满二叉树。如下图所示 :
③完全二叉树——在满二叉树的前提下,从树的最下层最右边开始连续删除若干个结点,最后形成的树就是完全二叉树。即,除了最后一层外,其余层都是满结点。所以可以说,满二叉树就是完全二叉树的一种特例(一个结点不删)。完全二叉树如下图所示 :
3° 森林——n个互不相交的树的集合。(整体上称为森林)如下图所示 :
4.相关应用 :
1° 树是数据库中数据组织的一种重要形式。
2° 操作系统中子父进程的关系本身就是一棵树。
3° 面向对象语言中类的继承关系本身就是一棵树。
4° 哈夫曼树(最优树)是对树的重要应用。
二、树的存储
1.二叉树的存储 :
1° 二叉树连续存储
因为二叉树不是线性结构,因此——要用线性结构存储非线性结构,如果仅仅存储有效的结点,无法判断连续存储中谁先存谁后存的问题(解决方法——先序中序后序);而且,如果仅仅存储有效的结点,无法根据所存的结点推断出树原先的形状。
所以,连续存储时,必须要求当前二叉树提前转化为完全二叉树。
Δ完全二叉树的两个优点——
①将不存在的结点虚拟化,相当于每个结点都有编号,那么根据当前结点的编号就可以推算出当前结点在树的第几层。
②查找某个结点的父结点和字结点速度很快,判断某结点有没有子结点速度也很快。
Δ完全二叉树的缺点——
①所需内存空间大,有内存的浪费。
2° 二叉树链式存储(常用)
链式存储,即像链表一样离散存储,如下图所示 :
树中的每个结点都分为了三部分——第一部分指向左子结点;第二部分用于保存有效数据;第三部分指向右子结点。
链式存储可以轻松解决连续存储中遇到的两个难题,因此链式存储较为简单。并且,链式存储可以仅存放有效结点,减少了内存空间的浪费,n个结点最多只浪费n + 1个内存空间。(空指针域的浪费)
2.普通树和森林的存储 :
1° 普通树的存储
同样是为了解决非线性结构用线性结构来存储的问题,常见的存储方式有4中——
①“双亲表示法” :
用结构体类型表示结点类型,在该结构体类型的数组中,每个结点元素分为两部分,一部分用于存放当前结点的数据,另一部分用于存放父结点的下标(其中,由于根结点没有父结点,因此根结点元素中存放的下标为-1)。如下图所示 :
②“孩子表示法” :
孩子表示法是一个“数组 + 链表”的格式,与双亲表示法类似,仍然是一个结构体类型的数组,只不过每个元素的第二部分变成了一个指针域,可以将子结点挂载到后面形成链表,如下图所示:
③“双亲孩子表示法” :
“双亲表示法”求父结点方便;“孩子表示法”求子结点方法。而“双亲孩子表示法”则同时兼具了“双亲表示法”和“孩子表示法”的优点。在“双亲孩子表示法”中,每个结点元素被分成了三部分,第一部分用于存储当前结点本身的有效数据,第二部分用于存储父结点的下标,第三部分是用于挂载子结点的指针域。说白了,就是把上面两种方法合起来了。如下图所示 :
④二叉树表示法 : (常用)
“双亲孩子表示法”虽然牛逼,但是不易通过程序来实际操作,因此平时使用更多的是“二叉树表示法”,顾名思义,就是将当前树转化为一棵二叉树,再进行存储。
一棵普通树转化为一棵二叉树的方法如下 :
任意一个结点需要满足两个条件——①左指针域指向它的第一个孩子(第一个子结点);②右指针域指向指向它的下一个兄弟。如下图所示 :
2° 森林的存储
森林的存储和普通树类似,都使用了二叉树表示法,需要将森林先转换为二叉树。
森林转化为二叉树的方法同普通树转化为二叉树的方法类似 :
唯一不同的地方在于,需要先将森林中的树互相看作兄弟,那么就将森林转化为了一棵“没有根结点的树”;然后再按照普通树转化为二叉树的方法进行转化即可。如下图所示 :
三、树的遍历
1.二叉树先序遍历 :
先序遍历遵循三个原则——
①先访问根结点;
②再遍历左子树;
③再遍历右子树;
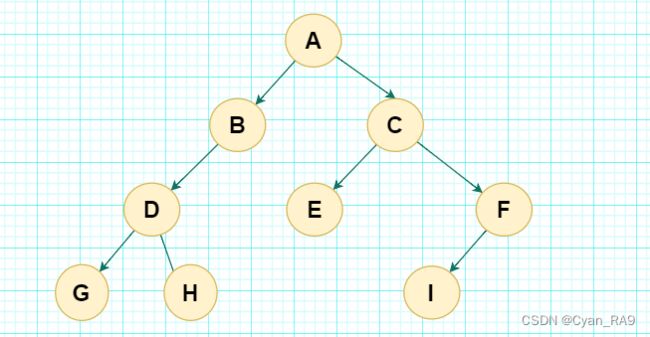
举个例子——如下图所示 :
上图是一棵普通二叉树,如果对它进行先序遍历,访问结果如何呢?
①首先访问整棵树的根结点A;
②然后先序访问A的左子树;A的左子树的根结点是D,所以接下来要访问D;
③接着访问D的左子树;D的左子树的根结点是I,所以接下来要访问I;接着访问I的左子树,因为I的左子树为空,所以接着访问I的右子树;因为I的右子树也为空,所以“I”这棵树访问完毕;I子树访问完毕,代表D的左子树访问完毕,接下来要访问D的右子树;
④又因为D的右子树也是一棵子树,所以要先访问该子树的根结点E;因为E子树的左子树为空,右子树也为空,所以E子树访问完毕;E子树访问完毕,代表D子树的左右子树都访问完毕;D子树访问完毕,代表A树的左子树访问完毕。
⑤接下来要访问A的右子树B;先访问根结点B;
⑥然后再访问B子树的左子树;因为B子树的左子树也是一棵树,所以要访问B子树的左子树的根结点F;
⑦接着,访问F子树的左子树J;先访问根结点J,因为J的左右子树都为空,所以J子树访问完毕;
⑧J子树访问完毕,代表F的左子树访问完毕,接下来要访问F子树的右子树;又因为F子树的右子树也是一棵树,所以接下里要访问根结点G;因为G子树的左右子树都为空,所以G子树访问完毕;G子树访问完毕,代表F子树的右子树访问完毕;F子树的右子树访问完毕,代表F子树访问完毕,代表B子树的左子树访问完毕;
⑨接下来要访问B子树的右子树,首先访问B子树的右子树的根结点C;
⑩再访问C子树的左子树,C子树的左子树为H,访问根结点H,因为H子树的左右子树均为空,所以H子树访问完毕;H子树访问完毕,代表了C子树的左子树访问完毕,接下来访问C子树的右子树;又因为C子树的右子树为空,所以C子树访问完毕;C子树访问完毕,代表B子树的右子树访问完毕;B子树的右子树访问完毕,代表B子树访问完毕;B子树访问完毕,代表A树的右子树访问完毕;A树的右子树访问完毕,代表A树访问完毕,即整棵树访问完毕。
最后的访问顺序是——ADIEBFJGCH。如下图所示 :
先序遍历的底层原理 :
用到了递归的思想!当我们想先序遍历某棵树时,必须首先去先序遍历该树的左子树,而要想遍历该树的左子树,又得去先序遍历该左子树的左子树,依次递归下去,直到某棵左子树的左子树为空了,再去遍历该子树的右子树,然后再递归回去,直到把整棵树遍历完毕。
2.二叉树中序遍历 :
中序遍历遵循三个原则——
①先遍历左子树;
②再访问根结点;
③再遍历右子树;
举个例子——如下图所示 :
上图是一棵普通二叉树,如果对它进行中序遍历,访问结果如何呢?
①先访问A的左子树D,又因为D不是一棵空树,所以要先访问D的左子树I,因为I的左子树为空,所以最先访问的是I子树的根结点I;
②接着,再访问I子树的右子树,因为I子树的右子树为空,所以I子树访问完毕;I子树访问完毕,代表D子树的左子树访问完毕,接下来访问根结点D;
③继续,遍历D的右子树,因为D的右子树E的左子树为空,所以接下来访问E子树的根结点E;
④然后,遍历E的右子树,因为E的右子树H的左子树为空,所以要访问根结点H;又因为H子树的右子树也为空,所以H子树遍历完毕;H子树遍历完毕,代表E子树的右子树遍历完毕;E子树的右子树遍历完毕,代表E子树遍历完毕,代表D子树的右子树遍历完毕;D子树的右子树遍历完毕,代表D子树遍历完毕,代表A树的左子树遍历完毕;
⑤所以接下来要访问A树的根结点A;
⑥继续,访问A树的右子树B,因为B子树的左子树不为空,所以要访问B子树的左子树F;又因为F的左子树为空,所以访问根结点F;又因为F子树的右子树为空,所以F子树遍历完毕;
⑦F子树遍历完毕,代表B子树的左子树遍历完毕,接下来访问B子树的根结点B;最后,遍历B子树的右子树,因为B子树的右子树为空,所以B子树遍历完毕;B子树遍历完毕,代表A树的右子树遍历完毕,整棵树遍历完毕。
最后的访问顺序是——IDEHAFB。如下图所示 :
3.二叉树后序遍历 :
后序遍历遵循三个原则——
①先遍历左子树;
②再遍历右子树;
③再访问根结点;
举个例子——如下图所示 :
上图是一棵普通二叉树,如果对它进行后序遍历,访问结果如何呢?
①先访问A树的左子树D,因为D也有左子树,所以先访问D树的左子树I;又因为I子树的左右子树均为空,所以最先访问的是I子树的根结点I;
②I子树访问完毕,代表D子树的左子树访问完毕;接下来访问D子树的右子树H,H与I同理,所以要访问根结点H;
③H子树访问完毕,代表D子树的右子树访问完毕;接下来访问D子树的根结点D;
④D子树访问完毕,代表A树的左子树遍历完毕,接下来要遍历A树的右子树B;B子树的左子树F不为空,所以要先遍历F子树;又因为F子树的左子树为空,所以接下来访问F子树的右子树的根结点G;
⑤G子树访问完毕,代表F子树的右子树访问完毕,所以接下来访问F子树的根结点F;
⑥F子树遍历完毕,代表B子树的左子树遍历完毕,接下来要遍历B子树的右子树C,所以接下来要访问的是B子树的右子树C的根结点C;
⑦C子树遍历完毕,代表B子树的右子树遍历完毕,接下来访问根结点B;
⑧B子树遍历完毕,代表A树的右子树遍历完毕,所以最后访问的是A树的根结点A;整棵树后序遍历完毕。
最后的访问顺序是——IHDGFCBA。如下图所示 :
其实,总结一下不难发现——二叉树的先序遍历,中序遍历和后序遍历,最大的区别就是对根结点的访问顺序不同。先序遍历先访问根结点(根左右);中序遍历中间访问根结点(左根右);后序遍历最后访问根结点(左右根);而三者对于左右树的访问顺序是一致的,都是先左后右。
四、树的还原
1.概述
无论是先序,中序还是后序遍历,仅通过一棵二叉树的一种遍历结果,都无法还原出原本的二叉树。但是,假若我们可以得知某个二叉树的先序序列和中序序列,或者中序序列和后序序列,我们就可以推算出原始的唯一确定的一棵二叉树。(PS : 通过先序序列和后序序列也无法还原出原始的二叉树,即必须有一个是中序序列)。
2.已知先序和中序求后序 :
已知某棵二叉树的先序序列和中序序列,要想求出对应的后序序列,本质上还是要先还原出原始的二叉树,然后再去求它的后序序列。
Δ方法 :
1° 根据先序遍历“根左右”的特点,先序序列中先出现的结点一定是根结点;
2° 根据中序遍历“左根右”的特点,每个根结点的左面的结点一定位于该根结点的左子树上;每个根结点的右面的结点一定位于该根结点的右子树上。若中序序列中,某个根结点的左面或右面没有其他非根结点,说明该根结点的左子树或右子树为空。
Δ举栗 :
若已知某二叉树的先序序列为: ABDGHCEFI;中序序列为:GDHBAECIF。请画出该二叉树的初始形态,并求出其后序序列。
答 :
首先,根据先序序列“根左右”的特点,先序序列中第一个结点为A,说明A结点是整棵二叉树的根结点;
其次,根据中序遍历“左根右”的特点,中序序列中A结点左面的结点“GDHB”就一定在A结点的左子树上,而A结点右面的结点“ECIF”就一定在A结点的右子树上;
我们先来看A树的左子树。已知“GDHB”一定在A树的左子树上,那么谁是A树左子树的根结点?回到先序序列,“GDHB”在先序序列中先出现的是B结点,所以B结点就是A树左子树的根结点;再来到中序序列,“GDHB”中,“GDH”均在B的左面,说明B结点的左子树不为空且由“GDH”这三个结点组成;而“GDH”中,最先在先序序列出现的是D结点,说明D结点就是B子树的根结点;继续,再来到中序序列,“GDH”中,G在D左面,H在D右面,所以可知D的左子树和右子树分别为G和H;D子树搞定,则B子树的左子树搞定,又因为在中序序列中,B和A直接没有其他的结点了,说明B子树的右子树为空,至此整个A树的左子树可以画出来,如下图所示 :
我们再来看A树的右子树。已知“ECIF”一定在A结点的右子树上,因为在先序序列中,C最先出现,所以A结点右子树的根结点就是C;又因为中序序列“ECIF”中,E在C的左面,“IF”在C的右面,所以C子树的左子树为E,而“IF”一定在C子树的右子树上;又因为“IF”在先序序列中F先出现,所以F为C子树右子树的根结点,而中序序列中“IF”I在F的左面,则表示I是F结点的左子树。至此,我们可画出原始的完整的二叉树——A树的模样,如下图所示 :
接着,我们可以根据还原出的二叉树,写出它的后序序列——GHDBEIFCA。
3.已知中序和后序求原始二叉树 :
已知中序和后序求原始二叉树的方法,与已知先序和中序求原始二叉树的方法类似。只不过不同的地方在于——先序序列中是谁先出现谁是根结点;而后序序列中是谁后出现谁是根结点,反过来了。对于中序序列,仍然是根结点左面的结点位于该根结点的左子树上,根结点右面的结点位于该根结点的右子树上。
Δ方法 :
1° 根据后序遍历“左右根”的特点,后序序列中最后出现的结点一定是整棵树的根结点;
2° 根据中序遍历“左根右”的特点,每个根结点的左面的结点一定位于该根结点的左子树上;每个根结点的右面的结点一定位于该根结点的右子树上。若中序序列中,某个根结点的左面或右面没有其他非根结点,说明该根结点的左子树或右子树为空。
Δ举栗 :
若已知某二叉树的中序序列为:BDCEAFHG;后序序列为:DECBHGFA。请画出该二叉树的初始形态,并求出其先序序列。
答 :
首先,根据后序遍历“左右根”的特点,后序序列中最后一个结点为A,说明A结点是整棵二叉树的根结点;
其次,根据中序序列“左根右”的特点,中序序列中A结点左面的结点“BDCE”就一定在A结点的左子树上,而A结点右面的结点“FHG”就一定在A结点的右子树上;
我们先来看A树的左子树。"BDCE"这几个结点中,最后在后序序列出现的是B结点,说明B结点就是A树左子树的根结点;再回到中序序列,B结点左面没有其他结点,说明B结点的左子树为空,而B结点右边是"DCE"结点,说明B结点的右子树由“DCE”结点构成;继续,“DCE”中,最后在后序序列出现的是C结点,说明C结点是B结点的右子树的根结点;又因为中序序列中D在C左面,E在C右面,说明D和E分别为C结点的左右子树;至此,C子树搞定——>B子树的右子树搞定——>B子树搞定——>A子树的左子树搞定。我们可以先画出A树目前的样子,如下图所示 :
我们再来看A树的右子树。 “FHG”这几个结点中,最后在后序序列中出现的是F结点,说明F结点是A树右子树的根结点;又因为在中序序列中,“FHG”,F结点左面没有其他结点,说明F结点的左子树为空;F结点右面是“HG”结点,说明F结点的右子树不为空且由“HG”结点构成;根据后序序列中G结点后出现,说明G结点是F结点右子树的根结点。而中序序列中G结点右面没有其他结点,说明G结点的右子树为空,又因为H位于G左面,说明H是G结点的左子树的根结点。至此,G子树搞定——>F子树搞定——>A子树的右子树搞定。现在我们可以画出A树完整的原始的样子,如下图所示 :
五、树的程序演示
1.静态创建与遍历
以链式二叉树为例——
将如下二叉树静态创建出来并分别进行先序,中序和后序的遍历 :
代码如下 :
# include
# include
typedef struct BTreeNode
{
char data;
struct BTreeNode * pLeftChild;
struct BTreeNode * pRightChild;
} BTN, * PBTN; //B代表Binary,二进制
PBTN create_Tree(void);
void preTraversing(PBTN); //preorder,先序遍历
void inTraversing(PBTN); //inorder,中序遍历
void postTraversing(PBTN); //postorder,后序遍历
int main(void)
{
PBTN pTree = create_Tree();
printf("\n先序序列:");
preTraversing(pTree);
printf("\n中序序列:");
inTraversing(pTree);
printf("\n后序序列:");
postTraversing(pTree);
return 0;
}
PBTN create_Tree(void)
{
PBTN pA = (PBTN) malloc(sizeof(BTN));
PBTN pB = (PBTN) malloc(sizeof(BTN));
PBTN pC = (PBTN) malloc(sizeof(BTN));
PBTN pD = (PBTN) malloc(sizeof(BTN));
PBTN pE = (PBTN) malloc(sizeof(BTN));
pA->data = 'A';
pA->pLeftChild = pB;
pA->pRightChild = pC;
pB->data = 'B';
pB->pLeftChild = pB->pRightChild = NULL;
pC->data = 'C';
pC->pLeftChild = pD;
pC->pRightChild = pE;
pD->data = 'D';
pD->pLeftChild = pD->pRightChild = NULL;
pE->data = 'E';
pE->pLeftChild = pE->pRightChild = NULL;
return pA;
}
void preTraversing(PBTN pRoot)
{
if (NULL != pRoot)
{
printf("%c ", pRoot->data);
if (NULL != pRoot->pLeftChild)
preTraversing(pRoot->pLeftChild);
if (NULL != pRoot->pRightChild)
preTraversing(pRoot->pRightChild);
}
}
void inTraversing(PBTN pRoot)
{
if (NULL != pRoot)
{
if (NULL != pRoot->pLeftChild)
inTraversing(pRoot->pLeftChild);
printf("%c ", pRoot->data);
if (NULL != pRoot->pRightChild)
inTraversing(pRoot->pRightChild);
}
}
void postTraversing(PBTN pRoot)
{
if (NULL != pRoot)
{
if (NULL != pRoot->pLeftChild)
postTraversing(pRoot->pLeftChild);
if (NULL != pRoot->pRightChild)
postTraversing(pRoot->pRightChild);
printf("%c ", pRoot->data);
}
} 运行结果 :
2.动态创建与遍历
动态创建二叉树,即二叉树的结点分配由程序员自主设计。
代码如下 :
# include
# include
# include
typedef struct BTreeNode
{
char data;
struct BTreeNode * pLeftChild, * pRightChild;
} BTN, * PBTN; //B代表Binary,二进制
PBTN create_Tree(PBTN);
void preTraversing(PBTN); //preorder,先序遍历
void inTraversing(PBTN); //inorder,中序遍历
void postTraversing(PBTN); //postorder,后序遍历
int main(void)
{
PBTN pTree = NULL;
pTree = create_Tree(pTree);
printf("\n先序序列:");
preTraversing(pTree);
printf("\n中序序列:");
inTraversing(pTree);
printf("\n后序序列:");
postTraversing(pTree);
return 0;
}
PBTN create_Tree(PBTN pRoot)
{
char value; //临时变量,用于表示当前结点的数据域
PBTN p; //临时变量,用于表示当前结点的指针
printf("请输入结点的值:value = ");
scanf("%c", &value);
getchar();
/*
getchar()这行代表很重要,
因为Windows操作系统中,输入Enter键达到的效果是"\r\n",
所以需要getchar()函数来吃掉后面的'\n',不然会直接将
剩下的\n赋值给下一次调用create_Tree函数时的value,使得运行结果达不到预期。
*/
if ('#' == value)
return NULL;
/*
当用户输入'#'时,返回NULL给主调函数,
表示上一级结点没有左孩子或者右孩子。
*/
p = (PBTN) malloc(sizeof(BTN));
if (NULL != p)
{
p->data = value;
}
else
{
printf("动态分配内存失败!");
exit(-1);
}
if (!pRoot)
pRoot = p; //如果当前根结点为空,就创建根结点。
printf("\n请输入%c结点的左子树的根结点\n", value);
p->pLeftChild = create_Tree(pRoot); //递归创建左子树
printf("\n请输入%c结点的右子树的根结点\n", value);
p->pRightChild = create_Tree(pRoot); //递归创建右子树
return p;
}
void preTraversing(PBTN pRoot)
{
if (NULL != pRoot)
{
printf("%c ", pRoot->data);
if (NULL != pRoot->pLeftChild)
preTraversing(pRoot->pLeftChild);
if (NULL != pRoot->pRightChild)
preTraversing(pRoot->pRightChild);
}
}
void inTraversing(PBTN pRoot)
{
if (NULL != pRoot)
{
if (NULL != pRoot->pLeftChild)
inTraversing(pRoot->pLeftChild);
printf("%c ", pRoot->data);
if (NULL != pRoot->pRightChild)
inTraversing(pRoot->pRightChild);
}
}
void postTraversing(PBTN pRoot)
{
if (NULL != pRoot)
{
if (NULL != pRoot->pLeftChild)
postTraversing(pRoot->pLeftChild);
if (NULL != pRoot->pRightChild)
postTraversing(pRoot->pRightChild);
printf("%c ", pRoot->data);
}
} 运行效果 : (如下GIF图)
最后该二叉树的遍历结果如下图所示 :
可以看到,其实up就是把上面静态构建二叉树的实例又给大家演示了一遍。当然,为了确定我们的程序能正常运行,这次up瞎写一个,如下GIF图所示 :
我们可以根据先序序列和中序序列画出我们设计的二叉树,如下图所示 :
嗯,看着还不错。