ViT 论文与代码阅读笔记

ViT 论文与代码阅读笔记

拒绝机翻论文，没有自己的理解翻译了也没有用吧。

简介

ViT 是谷歌团队发表与于 ICLR2021 的一篇文章，其内容主要就是将纯 Transformer 应用于视觉领域。

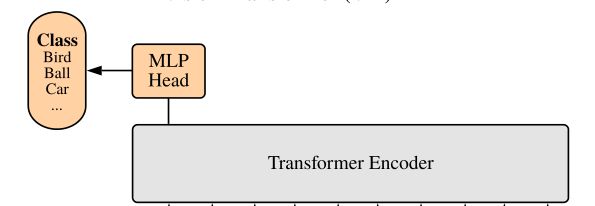
以下是 ViT 的网络结构图：

可以看到该网络中不包含 CNN，作者证明了传统的视觉任务中并不一定需要依赖于 CNN 结构，纯 Transformer 也能够很好地完成图像的分类任务。作者通过实验，在多个数据集上与 ResNet152 进行比较，均得到了更优的结果：

原版代码为 Jax 编写，地址： https://github.com/google-research/vision_transformer

github 另一位大佬提供了 PyTorch 版本，目前已有 9.2k stars： https://github.com/lucidrains/vit-pytorch

网络结构

Patch Embedding

首先是该部分，该部分就是将一张尺寸为 $H\times W\times C$图像，分为 $N$ 个 Patch，每个 Patch 的尺寸为 $P\times P$。说白了就是将大图像分割成 $N$ 小块个图像，$N=HW/P^2$ 。

例如一张 $224\times 224\times 3$ 的图像，设定 $P=16$ ，则 $N=196$ ，原图被分为 196 小块图像。

接着，将得到的小块图像展开变为 $N\times (P\times P\times C)$ ，在使用一个线性投影至 $N\times D$ ，以上部分的代码如下：

c, h, w = img.shape
pd = c * ph * pw

to_patch_embedding = nn.Sequential(
	Rearrange('b c (nh p1) (nw p2) -> b (nh nw) (p1 p2 c)', p1 = ph, p2 = pw),
	nn.Linear(pd, d)
)

embedded_img = to_patch_embedding(img)

以上步骤就将二维的图片转换为多组一维的序列以传入 Transformer 。

Positional Embedding & Extra Learnable [class] Embedding

ViT 与BERT 相同还需要加入一个 class token，这是最后用于传入 MLP 中以对图像进行分类的一个 token。其实现方法即为在得到的序列前另 concat 一条序列，其长度与图像信息的序列相同。

例如图像提取后为 196 组长度为 768 的序列，即尺寸为 $196\times 768$， 则需要随机生成一个 $1\times 768$ 的向量，并与图像信息序列做 concat 操作，最终得到的图像信息序列尺寸即为 $197\times 768$ 。

同时，ViT 为从图像提取的序列添加了位置编码，该位置编码是一个可学习的矩阵，其添加方式为直接加于原序列信息之上。

例如在经过上一步操作后得到了 $197\times 768$ 的图像信息序列，则需要随机生成一组尺寸同样为 $197\times 768$ 的位置信息矩阵，这里使用 sum 操作进行添加。

这里给出文中的公式：
$$z_0=[x_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s}};x_p^1\mathrm{E};{\mathrm{x}}_{\mathrm{p}}^2\mathrm{E};\cdots ,{\mathrm{x}}_{\mathrm{p}}^{\mathrm{N}}\mathrm{E}]+{\mathrm{E}}_{\mathrm{p}\mathrm{o}\mathrm{s}}$$
其中 $\mathrm{E}$ 为投影矩阵，${\mathrm{E}}_{\mathrm{p}\mathrm{o}\mathrm{s}}$ 为位置编码矩阵，$x_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s}}$ 为 class token。

以上步骤的代码如下所示：

pos_embedding = nn.Parameter(torch.randn(1, n + 1, dim))
cls_token = nn.Parameter(torch.randn(1, 1, dim))

cls_tokens = repeat(cls_token, '1 n d -> b n d', b = b)  # b is batch_size
embedded_img = torch.cat((cls_tokens, embedded_img), dim=1)
embedded_img += pos_embedding

Transformer Encoder

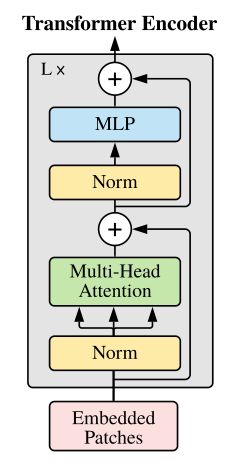
经过上面的 Embedding 处理，接着就是把 Embedded Patches 传入 Transformer Encoder 中了。

这里给出论文中的公式：
$$z_l^{\prime }=\mathrm{M}\mathrm{S}\mathrm{A}(\mathrm{L}\mathrm{N}({\mathrm{z}}_{\mathrm{l}-1}))+{\mathrm{z}}_{\mathrm{l}-1}$$
即，输入的 Embedded Patches 首先经过一个 LN（Layernorm）层，再通过一个 MHA （Multi-Head Attention）层。

LN 不同与 BN，BN是对整个 batch 进行归一化操作，而是对一条样本进行归一化操作，其公式如下：
$$y=\frac{x-E(x)}{\sqrt{V(x)+ϵ}}\ast \gamma +\beta$$
其中 $ϵ$ 是一个很小的数防止分母为 0，$\gamma$ 和 $\beta$ 是随着训练变化的数，默认为 1 和 0。

MSA的内部结构下图展示：

MSA 的代码如下：

class Attention(nn.Module):
    def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim = -1)
        self.dropout = nn.Dropout(dropout)

        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        attn = self.attend(dots)
        attn = self.dropout(attn)

        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

该类的实例化参数中，heads 为多头的数量，dim_head 为多头的维度。

类中定义了一个参数 self.to_qkv 是将图像信息序列转换为 $q,k,v$ 的矩阵，其尺寸为 $D\times (D_{head}\times N_{head})$ ，能够一次性将信息转换为 $q,k,v$，之后的 chunk 操作将 $q,k,v$ 分割成一个元组，即 $\mathrm{q}\mathrm{k}\mathrm{v}=(\mathrm{q},\mathrm{k},\mathrm{v})$ 。

q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)

由于目前 $q,k,v$ 尺寸均为 $D/3\times (D_{head}\times N_{head})$ ，后一个维度包含了$N_{head}$ 个头，为了后续的计算，需要将该维度分离出来，即从 b d (dh nh) -> b nh d dh。

根据 self-attention 的计算图，首先计算 $q$ 与 $k$ 的相似度，并除以一个 scaling factor（为了梯度稳定，但我还未理解其含义）。然后使用 softmax 归一化得到权重。再使用该权重与 $v$ 进行加权求和，得到输出。

则可以得到代码：

dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale
attn = self.attend(dots)
attn = self.dropout(attn)    # 非必要，默认的 attn 为 0

out = torch.matmul(attn, v)

最后，需要将尺寸变换回与输入时相同。由于使用了多头增加了一维，因此需要再从 b nh d dh 转回 b d (dh nh) 。考虑使用多头或多头的维度与原信息序列维度不一致时，即 (dh nh)!= d 时，还需要增加一个线性变换使其回到原来的维度，代码如下：

self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()
        
out = rearrange(out, 'b h n d -> b n (h d)')
out = self.to_out(out)

另外可以看到 Transformer 中使用了跳接的形式：

因此还需要以下操作：

attned_img = attn(embedded_img) + embedded_img

上半部分，再次进入一个 LN 层后，将进入一个 MLP 层，公式如下：
$$z_l=\mathrm{M}\mathrm{L}\mathrm{P}(\mathrm{L}\mathrm{N}(({\mathrm{z}}_{\mathrm{l}}^{\prime })))+{\mathrm{z}}_{\mathrm{l}}^{\prime }$$
其中 $z_l^{\prime }$ 为 MSA 部分的输出。论文中指出， MLP 包含两层，并有一个 GELU 的激活函数，其代码如下：

class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout = 0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim),
            nn.Dropout(dropout)
        )
    def forward(self, x):
        return self.net(x)

这一部分我觉得没啥好说的很简单，然后这一部分同样的使用了跳接。

mlped_img = ff(attned_img) + attned_img

则 Transformer Encoder 即为以上两个单元的堆叠，即 $(\mathrm{M}\mathrm{S}\mathrm{A}+\mathrm{M}\mathrm{L}\mathrm{P})\times \mathrm{L}$ 。

最后就是一个 MLP Head 进行预测了，代码如下：

self.mlp_head = nn.Sequential(
	nn.LayerNorm(dim),
	nn.Linear(dim, num_classes)
)

self.mlp_head(x)

没啥好说的，那么ViT 的论文与代码的阅读就到此为止。