AcWing 245：你能回答这些问题吗 ← 线段树

【题目来源】
AcWing 245. 你能回答这些问题吗

【算法分析】
针对线段树不同类型问题的算法设计，一种观点认为“首先就是针对问题确定线段树的结点结构属性，之后的任务就直剩套线段树的代码模板了”。个人认为，此观点蛮精辟的。
由于线段树的结点具有多个属性，所以可将query()函数的返回类型定义为线段树的node类型，这样就可以按需查看线段树的任何返回属性值了。
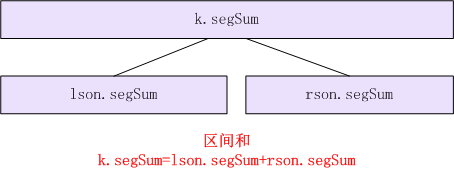
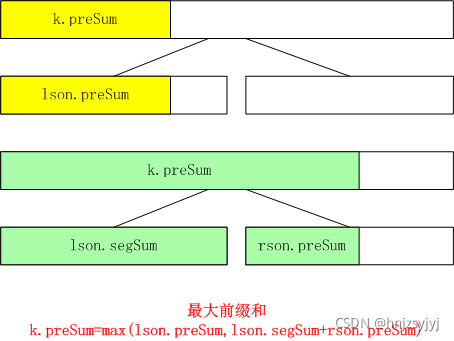
关于本题所涉及到的区间和、最大前缀和、最大后缀和、最大连续子段和的相关情况示意如下：

---

---

---

 

---

【算法代码】 

#include
using namespace std;

const int maxn=500005;
int a[maxn];

struct node {
    int le,ri;
    int segSum; //区间和
    int preSum; //最大前缀和
    int sufSum; //最大后缀和
    int maxSum; //最大连续子段和
} tree[maxn*4];

void pushup(node &k, node &lson, node &rson) {
    k.segSum=lson.segSum+rson.segSum;
    k.preSum=max(lson.preSum,lson.segSum+rson.preSum);
    k.sufSum=max(rson.sufSum,rson.segSum+lson.sufSum);
    k.maxSum=max(max(lson.maxSum,rson.maxSum),lson.sufSum+rson.preSum);
}

void pushup(int k) {
    pushup(tree[k], tree[k<<1], tree[k<<1|1]);
}

void build(int k, int le, int ri) {
    if(le==ri) tree[k]= {le, ri, a[le], a[le], a[le], a[le]};
    else {
        tree[k]= {le,ri};
        int mid=(le+ri)>>1;
        build(k<<1,le,mid), build(k<<1|1, mid+1, ri);
        pushup(k);
    }
}

void update(int k, int i, int v) { //单点更新
    if(tree[k].le==i && tree[k].ri==i) tree[k]= {i,i,v,v,v,v};
    else {
        int mid=(tree[k].le+tree[k].ri)>>1;
        if(i<=mid) update(k<<1,i,v);
        else update(k<<1|1,i,v);
        pushup(k);
    }
}

node query(int k, int le, int ri) { //区间查询
    if(tree[k].le>=le && tree[k].ri<=ri) return tree[k];
    else {
        int mid=(tree[k].le+tree[k].ri)>>1;
        if(ri<=mid) return query(k<<1,le,ri);
        else if(le>mid) return query(k<<1|1,le,ri);
        else {
            node ans;
            node left=query(k<<1,le,ri);
            node right=query(k<<1|1,le,ri);
            pushup(ans,left,right);
            return ans;
        }
    }
}

int main() {
    int n,m;
    cin>>n>>m;
    for(int i=1; i<=n; i++) scanf("%d",&a[i]);

    build(1, 1, n);

    while(m--) {
        int op,x,y;
        cin>>op>>x>>y;
        if(op==1) {
            if(x>y) swap(x,y);
            cout<

【参考文献】
https://blog.csdn.net/qq_44791484/article/details/113827997
https://blog.csdn.net/hnjzsyjyj/article/details/120590584
https://www.acwing.com/problem/content/description/246/
https://www.acwing.com/video/649/