二叉树前中后层遍历(递归/非递归)(简单易懂(*^ｰ^))

二叉树的遍历

1 先序遍历

1.1 递归

先序遍历(Preorder Traversal)，即根左右的顺序遍历树。递归代码如下：

void preorder(Btree T)//递归先序遍历
{
	if(T)	//判断结点是否为空
	{
		visit(T);   //访问根结点
		preorder(T->lchild);	//递归遍历左子树
		preorder(T->rchild);	//递归遍历右子树
	}
}

1.2 非递归

对于非递归的先序遍历，借助栈来辅助。非递归代码如下：

void preorder2(BiTree T){//非递归先序遍历
    InitStack(S);	//初始化栈S
    BiTree p = T;	//p作为遍历指针
    	while(p || !isEmpty(S)){	//栈不空或p非空就继续循环
            if(p){	//一路向左	
                visit(p);	//访问当前结点
                Push(S, p);	//将当期那结点入栈
                p = p->lchild;	//左孩子非空，就一直向左走
            }
            else{
                Pop(S, p);	//栈顶元素出栈
                p = p->rchild;	//向右子树走，p赋值为当前结点的右孩子
            }      
        }	
}

2 中序遍历

2.1 递归

中序遍历(Inorder Traversal)，即左根右的顺序遍历树，递归代码如下：

void inorder(BiTree T){	//递归中序遍历
	if(T){
		inorder(T->lchild);
		visit(T);
		inorder(T->lchild);
	}
}

2.2 非递归

对于非递归的中序遍历，借助栈来辅助。非递归代码如下：

void inorder2(BiTree T){	//非递归中序遍历
	InitStack(S);
	BiTree p = T;
	while(p || !IsEmpty(S)){
		if(p){
			Push(S, p);
			p = p->lchild;	//左
		}
		else{
			visit(p);	//根
			Pop(S, p);
			p = p->rchild;	//右
		}
	}
}

3 后序遍历

3.1 递归

后序遍历(Postorder Traversal)，即左右根的顺序遍历树，递归代码如下：

void postorder(BiTree T){
	if(T){
		postorder(T->lchild);
		postorder(T->rchild);
		visit(T);
	}
}

3.2 非递归

对于非递归的后序遍历，借助栈来辅助。

​ 需要注意的是，后序非递归遍历算法和先序中序非递归遍历算法的思路有一点区别，后序非递归算法在visit一个结点时，需要保证左孩子与右孩子都已被访问，并且左孩子需在右孩子之前被访问(左右根)。

于是何时可以visit一个结点，就有了以下 2 种情况：

1. 该结点的左右孩子均为空
2. 该结点的左右孩子不为空但都已被访问

对于一个结点是否被访问过，我们可以定义一个指针r来进行辅助。

非递归代码如下：

void postorder2(BiTree T){	//非递归后序遍历
    InitStack(S);
    BiTNode *p = T; 	//注：写成BiTree p = T;也可
    BiTNode *r = NULL;		//注：写成BiTree r = NULL;也可
    while(p || !IsEmpty(S)){
        if(p){
            Push(S, p);
            p = p->lchild;	//左
        }
        else{
            GetTop(S, p);	//查看栈顶元素
            if(p->rchild && p->rchild != r){	//如果右孩子存在且没被访问过
                p = p->rchild;	//右
            }
            else{
                visit(p);	//根
                Pop(S, p);
                r = p;	//记录刚刚访问过的结点
                p = NULL;	//结点访问完，p置空以便继续回溯到其父节点进行后序遍历
            }
        }
    }
}

4 层序遍历

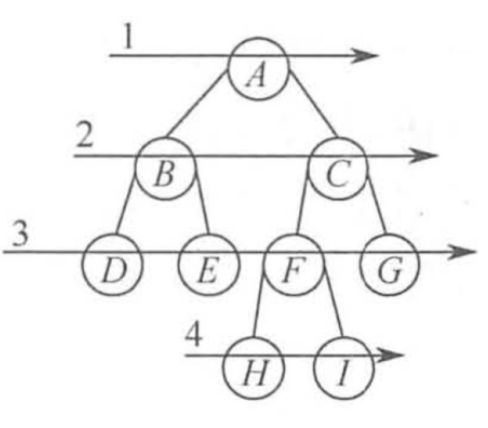
层序遍历(Level Order Traversal)，即从上至下，从左到右，一层一层地访问结点：

图1 二叉树的层序遍历

对于二叉树的层序遍历，借助队列来辅助。代码如下：

void levelorder(BiTree T){
    InitQueue(Q);	//初始化辅助队列
    BiTree p;
    EnQueue(Q, T);	//根结点入队
    while(!IsEmpty(Q)){	//队列不为空则循环
        DeQueue(Q, p);	//队头结点出队
        visit(p);	//访问出队的结点
        if(p->lchild != NULL)	//出队结点的左孩子非空
            EnQueue(Q, p->lchild);	//左孩子入队
        if(p->rchild != NULL)	//出队结点的右孩子非空
            EnQueue(Q, p->rchild);	//右孩子入队
    }
}

5 前中后层序完整可运行代码（C++）

#include 
#include //引入队列头文件
using namespace std;

typedef struct Bnode	/*定义二叉树存储结构*/
{ char data;
	struct Bnode *lchild,*rchild;
}Bnode,*Btree;

void Createtree(Btree &T)	/*创建二叉树函数*/
{
	//按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
	char ch;
	cin >> ch;
	if(ch=='#')
		T=NULL;			//递归结束，建空树
	else{
		T=new Bnode;
		T->data=ch;					//生成根结点
		Createtree(T->lchild);	//递归创建左子树
		Createtree(T->rchild);	//递归创建右子树
	}
}

void preorder(Btree T)//先序遍历
{
	if(T)
	{
		cout<<T->data<<"  ";
		preorder(T->lchild);
		preorder(T->rchild);
	}
}

void inorder(Btree T)//中序遍历
{
	if(T)
	{
		inorder(T->lchild);
		cout<<T->data<<"  ";
		inorder(T->rchild);
	}
}

void posorder(Btree T)//后序遍历
{
	if(T)
	{
		posorder(T->lchild);
		posorder(T->rchild);
		cout<<T->data<<"  ";
	}
}

bool Leveltraverse(Btree T)
{
	Btree p;
	if(!T)
		return false;
	queue<Btree>Q; //创建一个普通队列(先进先出)，里面存放指针类型
	Q.push(T); //根指针入队
	while(!Q.empty()) //如果队列不空
	{
		p=Q.front();//取出队头元素作为当前扩展结点livenode
		Q.pop(); //队头元素出队
		cout<<p->data<<"  ";
		if(p->lchild)
			Q.push(p->lchild); //左孩子指针入队
		if(p->rchild)
			Q.push(p->rchild); //右孩子指针入队
	}
	return true;
}

int main()
{
	Btree mytree;
	cout<<"按先序次序输入二叉树中结点的值（孩子为空时输入#），创建一棵二叉树"<<endl;
	Createtree(mytree);//创建二叉树
	cout<<endl;
	cout<<"二叉树的先序遍历结果："<<endl;
	preorder(mytree);//先序遍历二叉树
	cout<<endl;
	cout<<"二叉树的中序遍历结果："<<endl;
	inorder(mytree);//中序遍历二叉树
	cout<<endl;
	cout<<"二叉树的后序遍历结果："<<endl;
	posorder(mytree);//后序遍历二叉树
	cout<<endl;
	cout<<"二叉树的层次遍历结果："<<endl;
	Leveltraverse(mytree);//层次遍历二叉树
	return 0;
}

输入描述与示例

​ 这段代码包括创建二叉树、先序遍历、中序遍历、后序遍历和层次遍历。输入样例应该是一个字符串，其中每个字符代表一个节点的值，按照先序遍历的顺序输入。当输入字符为“#”时，表示该结点为空。

例如，对于一棵如下所示的二叉树：

    A
   / \
  B   C
 / \   \
D   E   F

输入样例应该是：ABD##E##C#F##。其中，A 是根节点，B 是 A 的左子节点，D 是 B 的左子节点，# 表示 D 的左子节点为空，接下来的 # 表示 D 的右子节点为空，以此类推。

运行结果

图2 代码运行结果