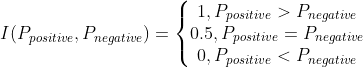Spark - AUC、Accuracy、Precision、Recall、F1-Score 理论与实战
一.引言
推荐场景下需要使用上述指标评估离、在线模型效果,下面对各个指标做简单说明并通过 spark 程序全部搞定。
二.指标含义
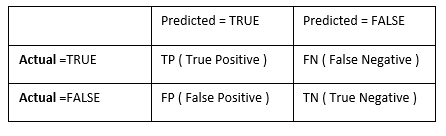
1.TP、TN、FP、FN
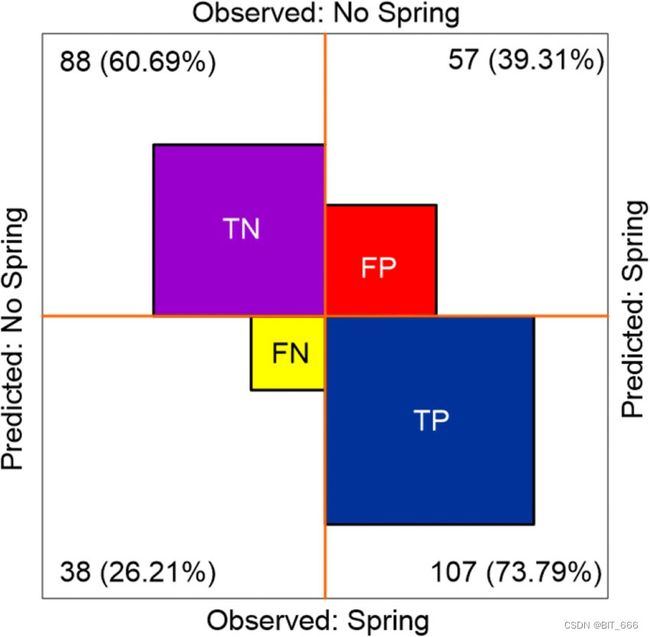
搜广推场景下最常见的就是 Ctr 2 分类场景,对于真实值 real 和预测值 pre 分别有 0 和 1 两种可能,从而最终 2x2 产生 4 种可能性:
- TP 真正率 对的预测对,即 1 预测为 1,在图中体现为观察与预测均为 Spring
- FP 假正率 错的预测对,即 0 预测为 1,在图中体现为 NoSpring 预测为 Spring
- FN 假负率 对的预测错,即 1 预测为 0,在图中体现为 Spring 预测为 NoSpring
- TN 真阴率 错的预测错,即 0 预测为 0,在图中体现为 NoSpring 预测为 NoSpring
整理后如下图所示:
2.Accuracy、Precision、Recall、F1-Score
根据上面提到的 TP、TN、FP、FN,有了上述几个指标的定义:
- Accuracy 准确率
即不管是0还是1,预测正确即可
- Precision 精度
即预测为1的样本中确实为1的样本比例,该指标只管预测为1的样本
- Recall 召回率
即样本中正样本有多少预测为正,该指标只管真实为1的样本
![]()
- F1-Score
平衡分数,用于定义 Precision 与 Recall 的调和平均数
- Fβ-Score
平衡分数,相比于 F1 更加灵活的调和平均数
通过调节 β 参数,可以使指标更偏向于不同的 metrics,β>1 例如 F2-Score 时,Recall 的权重高于 Precision,相反如果 β < 1例如 F0.5-Score 则 Precision 权重高于 Recall,这个把分子拆分开即可轻松得出结论。
3.AUC
AUC(Area Under Curve)被定义为ROC曲线下的面积,针对给定的一批对正负样本,用分类器分别预测一对正负样本,正样本预测概率大于负样本预测概率的概率即对应面积大小。
3.1 常规计算
假定这批样本中存在 M 个正样本,N 个负样本,分类器为 Tk,则 AUC 计算公式如下:
其中 P 的计算根据学习器 Tk:
![]()
I 为示性函数:
3.2 快速计算
上面是基础的 AUC 计算公式,由于需要对每一对正负样本预测概率进行比对,而实际场景下 M 与 N 都非常大从而造成运行速度缓慢的问题,优化后公式如下:
简单约分下:
这个公式也比较好理解,由于 AUC 并不关注分数而是关注正负样本的序,因此我们将全部预测样本排序,针对每个正样本,其序就代表了它超过了多少个样本的预测值,针对每个正样本可以得到总的序为:
但是由于每一次序的排列中,除了负样本外还有正样本,针对 rank 最高的正样本,其下有 M-1 个正样本,rank 第二高的,其下有 M-2 个正样本,依次类推,共有:
所以需要在 ∑ rank 的基础上再减去 (M-1)·M / 2,至于为什么有公式是 M·(M+1) 有的是 (M-1)·M,这个其实和你计算的序即 rank 是从 0 开始还是从 1 开始,如果从 1 开始,则等差数列求和公式结果就是 M·(M+1) 反之即为 (M-1)·M。
3.3 手推计算
按照 M-1 即从 0 开始的 rank 计算:
按照 M+1 即从 1 开始的 rank 计算:
最后用最原始的方法计算一下,即将所有组合进行遍历:
这里 I 为上面提到的示性函数。
Tips:
这里还有一种特殊情况即有多个正负样本分值相同,此时排序后其 rank 值可以取所有相同分数的 rank 值平均代表其 rank,不过在大数据且 CTR 精度较高条件下,这个 rank 带来的影响可以近似忽略。
三.Spark 实现
1.数据预处理
val rankResult = inputRdd.map { case (realLabel, preLabel, preScore) => {
// val preLabel = if (preScore > 0.5) "1" else "-1"
(realLabel, preLabel, preScore)
}
}.filter(_._3 >= 0)
rankResult.persist(StorageLevel.MEMORY_AND_DISK_SER_2)原始数据格式为 realLabel 和 preScore,这里可以通过 preScore + 阈值进行推理推断出 preLabel,即可得到三列元组的 RDD。实际计算过程中,你的 RDD 元祖只要有:
- Real Label 真实标签
- Predict Score 模型预测分
两个元素即可。
2.计算 TP、FP、FN、TN
/*
计算相关数值
TP: 真正率 对的预测对
FP: 假正率 错的预测对
FN: 假负率 对的预测错
TN: 真阴率 错的预测错
*/
val threshold = 0.5
val dataTP = rankResult.filter(x => x._1 == 1 && x._3 >= threshold).cache()
val dataFP = rankResult.filter(x => x._1 != 1 && x._3 >= threshold).cache()
val dataFN = rankResult.filter(x => x._1 == 1 && x._3 < threshold).cache()
val dataTN = rankResult.filter(x => x._1 != 1 && x._3 < threshold).cache()
val TP = dataTP.count()
val FP = dataFP.count()
val FN = dataFN.count()
val TN = dataTN.count()
val total = TP + FN + FP + TN根据定义计算指标即可:
- TP 真正率 对的预测对
- FP 假正率 错的预测对
- FN 假负率 对的预测错
- TN 真阴率 错的预测错
Tips:
这里阈值常规为 0.5,大家也可以根据自己场景的需求进行阈值调整,对于 AUC 而言,其计算只关注序不关注分数,而 TP、TN 这些指标则与阈值分数相关。其次这里一定要加 persist,否则性能会慢很多。
3.计算 Precision、Recall、Accuracy、F1-Score
基于 TP、FP、FN、TN 计算 Precision、Recall 与 Accuracy,最后计算 F1-Score,大家也可以自定义 β,实现 F-β 参数。
val Precision = if ((TP + FP) > 0) (TP * 1.0) / (TP + FP) else 0.0
val Recall = if ((TP + FN) > 0) (TP * 1.0) / (TP + FN) else 0.0
val Accuracy = if (total > 0) (TP + TN) * 1.0 / total else 0.0
val F1Score = if ((Precision + Recall) > 0.0) (2 * Precision * Recall) / (Precision + Recall) else 0.04.计算 AUC
// sort by predict
val sorted = rankResult.sortBy(x => x._3)
val numTotal = sorted.count() // M + N
val numPositive = rankResult.filter(x => x._1 == 1).count // M
val numNegative = numTotal - numPositive // N
val sumRanks = sorted.zipWithIndex().filter(x => x._1._1 == 1).map(x => x._2 + 1).reduce(_ + _)
val AUC = if (numNegative > 0 & numPositive > 0) {
sumRanks * 1.0 / numPositive / numNegative - (numPositive + 1.0) / 2.0 / numNegative
} else 0.0直接根据 predict 分排序即可,这也再次呼应前面 Tips 提到的,AUC 只关注正负样本的序,最后套用约分后的公式即可:
其中 M = numPositive,N = numNegative。
四.总结
AUC 评估的优点是:
- 对数据不平衡的情况有很好的适应能力,不受正负样本比例影响
- 评估结果简单,易于理解
- 不会受到分类器的阈值选择的影响
AUC 评估的缺点是:
- 不直接给出分类器的分类阈值
- 不适用于多分类问题
针对不同问题,除了 AUC 还有很多指标可供参考,大家需要根据自己的场景需求选择最优的评估指标,或者基于现有指标进行拓展。