云南专升本-数据结构知识总结和常考例题(二)
文章目录
- 四、串
- 五、数组和广义表
-
- 1.数组
- 2.广义表
- 六、树和二叉树
-
- 1.树
- 2.二叉树
四、串
-
串是由零个或多个字符组成的有限序列。
-
子串:串中任意个连续的字符组成的子序列称作该串的子串.
-
主串:包含子串的串相应的称为主串.
-
子串在主串中的位置:子串的第一个字符在主串中的位置表示.
-
空串:长度为零的串称为空串.
-
空格串:串中元素均为空格的串称为空格串.
-
串相等:长度相等且对应位置字符都相等.
串的存储结构
求串长:串中的字符个数 ,strlength()
串连接:strCat()
求子串:Substring()
主串首次出现的位置:Strindex()
eg1.串是一种特殊的线性表,其特殊行表现在()
A.可以顺序存储
B.数据元素是一个字符
C.可以链式存储
D.数据元素可以是多个字符
答案:B
eg2.串的长度是指()
A.串中所含不同字母的个数
B.串中所含字符的个数
C.串中所含不同字符的个数
D.串中所含非空格字符的个数
答案:B
判断题
串的链式存储与串的顺序存储相比在插入,删除操作上效率更高。(√)
五、数组和广义表
1.数组
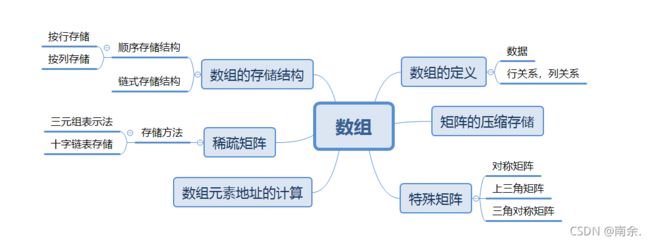
特殊矩阵:值相同的元素或者零元素在矩阵中的分布有一定规律的矩阵称为特殊矩阵.
稀疏矩阵:非零的数据元素个数很少的矩阵称为稀疏矩阵.
对称矩阵:一个n阶方阵,若满足a[i][j]=a[j][i],则称该矩阵为对称矩阵.
三角矩阵:主对角线上方和下方的元素(不包括对角线)均为常数或零元素的矩阵.
行表:记录稀疏矩阵中每行非零元素在三元组表中的起始位置的表.
三元组表:若线性表顺序存储的每一个结点均是三元组,则该线性表的存储结构称为三元组表.
带状矩阵:所有非零元素均集中在以主对角线为中心的带状区域的矩阵.
1.二维数组的两种存储方式:
以行为主序:按行优先求起始地址 A[i][j]=loc+(n*i+j)*x
loc:起始[0][0] x:元素个数 n:列
以列为主序:按列优先求起始地址 A[i][j]=loc+(m*j+i)*x
loc:起始[0][0] x:元素个数 m:行
2.广义表
一、广义表的长度和深度
长度:为表中最上层元素的个数
深度:为表中括号的最大层数
二、广义表的两个基本操作
1.取广义表表头GetHead:表中的第一个元素为此表的表头
2.取广义表表尾GetTail:表中除第一个外的其余元素组成的表为此表的表尾
任何一个非空广义表的表头可能是原子,也可能是广义表,而其表尾必定是广义表
eg1.数组通常具有的两种基本操作是()
A.查找和修改
B.查找和索引
C.索引和修改
D.监理和删除
答案:A
eg2.在以下叙述中正确的是()
A.线性表的顺序存储结构优于链表存储结构
B.二维数组是数据元素为线性表的线性表
C.栈的操作方式是先进先出
D.队列的操作是先进后出
答案:B
eg3.对特殊矩阵采用压缩存储的目的主要为了()
A.对矩阵元素的存取变得更简单
B.表达更简单
C.去掉矩阵中多余元素
D.节省存储空间
答案:D
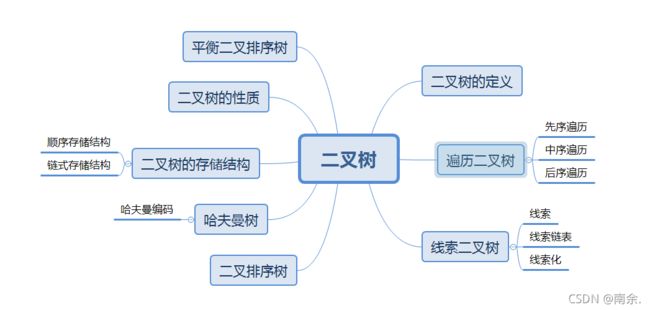
六、树和二叉树
1.树
树:是n个结点的有限集合,n≥0,有且只有一个称为根的结点,根结点无前驱.
森林:m(m≥1)棵互不相交的树的集合.
有序树:树中结点的各子树看成是从左至右依次有序的,且不能交换.
2.二叉树
二叉树常见的五种基本形态
3.二叉树的性质
性质1:非空二叉树上叶子结点数等于度为2的节点数加1,即N0=N2+1(N0:度为0,适用所有二叉树)
性质2:非空二叉树上第K层至多有2k-1个结点(k>=1),(至少有一个结点)
性质3:高度为H的二叉树至多有2H-1个结点(H>=1),(至少有H个结点)
性质4:具有N个结点的完全二叉树的高度为[ log2(N+1) ] (向上取整) 或 [ log2N ]+1 (向下取整)
性质5:对完全二叉树从上到下,从左到右的顺序依次编号1,2,…,N,则有一下关系:
a.当i=1,则序号为i的结点是根结点,无双亲结点
b.当2i<=N时,结点i的左孩子编号为2i,否则无左孩子
c.当2i+1<=N时,结点i的右孩子编号为2i+1,否则无右孩子
二叉树的遍历
1.先序遍历递归算法(根左右)
void PreOrder(BiTree T){
if(T!=Null){
visit(T);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
2.中序遍历递归算法(左根右)
void InOrder(BiTree T){
if(T!=Null){
PreOrder(T->lchild);
visit(T);
PreOrder(T->rchild);
}
}
3.后序遍历递归算法(左右根)
void PostOrder(BiTree T){
if(T!=Null){
PreOrder(T->lchild);
PreOrder(T->rchild);
visit(T);
}
}
4.层次遍历
考点:进行层次遍历需要借助一个队列
(1)删一个(出队)
(2)让p指向被删元素
(3)p指向左右孩入队
树及其转换
(一)、树转换为二叉树(左孩子右兄弟)
特点:1.树对应的二叉树正颗大树的根节点无右子树
2.树的先序遍历对应二叉树的先序遍历
3.树的后序遍历对应二叉树的中序遍历
(二)、森林转换为二叉树
森林与二叉树之间的对应关系
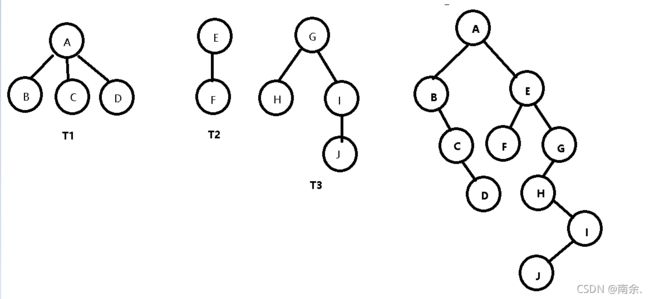
(1)以T1的根为二叉树的根
(2)其余的根(T2、T3)作为T1 的兄弟
(3)左孩子右兄弟
哈夫曼树(二叉树)
叶子结点带权路径长度 = 该结点权值 * 路径长度
树的带权路劲长度 = 叶子结点带权路径长度之和
wpl:最小的二叉树
判断题
1.树的三种常用的存储方法:孩子表示法,双亲表示法和孩子兄弟表示法.(√)
2.深度为k的二叉树中,结点总数最多为(2^k)-1个.(√)
3.哈夫曼树又称最优二叉树,是一类带权路径长度最短的树.(√)
4.满二叉树是一棵深度为k的,且有(2^k)-1个结点的二叉树.(√)
5.二叉树的任意结点最多有两颗子树(√)
对一颗具有n个结点的树,树中所有的度数之和为()
A.n B.n-2 C.n-1 D.n+1
答案:C
设在一颗度为4的树中,度数为4的结点数有4个,度数为3的结点数有2个,度数为2的结点数有2个,度数为1的结点数有5个,那么度数为0的结点数有()
A.17 B.18 C.19 D.20
答案:C
二叉树和度为2的树的相同之处包括()
A.每个结点都有一个或两个孩子结点
B.至少有一个根节点
C.至少有一个度为2的结点
D.每个结点至多只有一个双亲结点
答案:D
提示:连载中…