7-2 电路布线

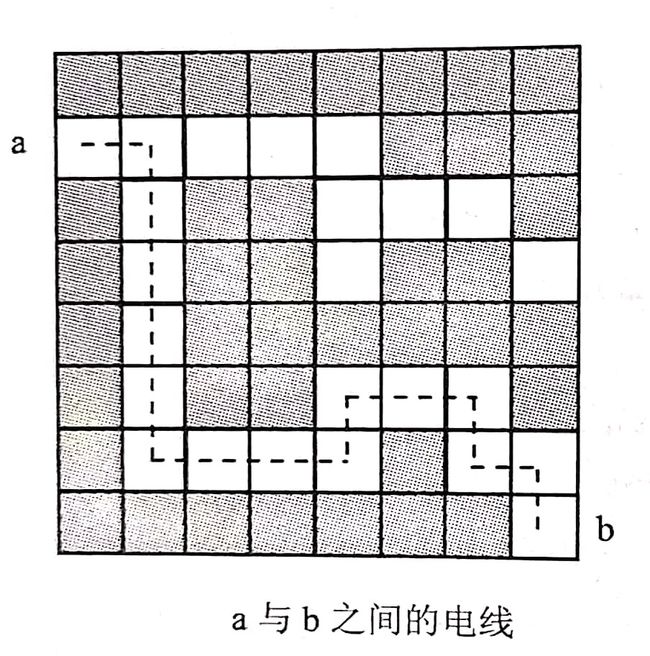
在解决电路布线问题时，一种很常用的方法就是在布线区域叠上一个网格，该网格把布线区域划分成m*n个方格，布线时，转弯处必须采用直角，如已经有某条线路经过一个方格时，则在该方格上不允许叠加布线。如下图所示，如从一个方格a(2，1)的中心点到另一个方格b（8,8）的中心点布线时， 每个方格布线时需要1个单位的电路材料，所需要最少的电路材料是16。

输入格式:

第一行输入网格的m和n

第二行开始输入网格中已经布线的情况，如果已经有布线时，用1表示，尚未布线时，用0表示。

接下来两行分别输入需要布线的起始位置a和结束位置b。

输出格式:

输出从起始位置a到结束位置b布线时所需要的最少电路材料。

输入样例:

在这里给出一组输入。例如：

8 8
1 1 1 1 1 1 1 1
0 0 0 0 0 1 1 1
1 0 1 1 0 0 0 1
1 0 1 1 0 1 1 0
1 0 1 1 1 1 1 1
1 0 1 1 0 0 0 1
1 0 0 0 0 1 0 0
1 1 1 1 1 1 1 0
2 1
8 8

输出样例:

在这里给出相应的输出。例如：

16

 对于求单一路径问题BFS效率远大于DFS

先提供BFS代码

#include 
using namespace std;
const int maxn = 1000;
int N, M, x, y, X, Y;
int MAP[maxn][maxn];
//BFS
class ans
{
public:
    int x;
    int y;
    int num;
    ans(int A, int B, int C)
    {
        x = A;
        y = B;
        num = C;
    }
};

void BFS(int x, int y)
{
    queueQ;
    ans* T = new ans(x,y, 1);
    Q.emplace(T);
    while (!Q.empty())
    {
        if (Q.front()->x == X && Q.front()->y == Y)
        {
            cout << Q.front()->num;
            break;
        }
        int dx[4] = { 1,-1,0,0 };
        int dy[4] = { 0,0,1,-1 };
        for (int i = 0; i < 4; i++)
        {
            int nx = Q.front()->x + dx[i], ny = Q.front()->y + dy[i];
            if (nx >= 1 && nx <= N && ny >= 1 && ny <= M && MAP[nx][ny] == 0)
            {
                MAP[nx][ny] = 1;
                ans* temp = new ans(nx, ny, Q.front()->num + 1);
                Q.emplace(temp);
            }
        }
        Q.pop();
    }
}

int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
    {
        for (int j = 1; j <= M; j++)
        {
            cin >> MAP[i][j];
        }
    }
    cin >> x >> y >> X >> Y;
    BFS(x, y);
    return 0;
}

2:DFS代码

#include 
using namespace std;
const int maxn = 1000;
int N, M, x, y, X, Y;
int MAP[maxn][maxn];
bool vis[maxn][maxn];
int ans1 = 9999;
void DFS(int x, int y, int num)
{
    if (x < 1 || x > N || y < 1 || y > M || MAP[x][y] == 1)
        return;
    if (x == X && y == Y) //只在终点更新答案
        ans1 = min(ans1, num);
    int dx[4] = { 0,0,1,-1 };
    int dy[4] = { 1,-1,0,0 };
    vis[x][y] = 1;
    for (int i = 0; i < 4; i++)
    {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 1 && nx <= N && ny >= 1 && ny <= M && MAP[nx][ny] == 0 && vis[nx][ny] == 0)
        {
            vis[nx][ny] = 1;
            DFS(nx, ny, num + 1);
            vis[nx][ny] = 0;
        }
    }
}
int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
    {
        for (int j = 1; j <= M; j++)
        {
            cin >> MAP[i][j];
        }
    }
    cin >> x >> y >> X >> Y;
    DFS(x, y, 1);
    cout << ans1 << endl;
}