Python 列表的真正工作原理

本文主要讨论世界上排名第一的数据结构：数组。 

如果你还不是数据结构专家，我保证你会更好地理解 Python 列表，包括其的优点和局限性。

如果您已经了解所有内容 —— 刷新关键点并没有什么坏处。

每个人都知道如何在 Python 中使用列表：

>>> guests = ["Frank", "Claire", "Zoe"]>>> guests[1]'Claire'

你肯定知道按索引选择一个项目（比如 guests[idx]），即使在一百万个元素列表上也能高效工作，立刻返回结果。

更准确地说，按索引选择需要固定时间 O (1)—— 也就是说，它不受于列表中的元素数量的影响。

你知道为什么它工作得这么快吗？让我们来了解一下。

目录

1. 列表 = 数组？

2. 复现一个非常原始的列表

3. 列表 = 指针数组

4. 列表 = 动态数组

5. 将项目附加到列表

为什么分摊附加时间是 O (1)

6. 总结

---

1. 列表 = 数组？

列表是基于数组的，数组是这样一组元素的集合：

1. 大小相同

2. 在内存中连续排列

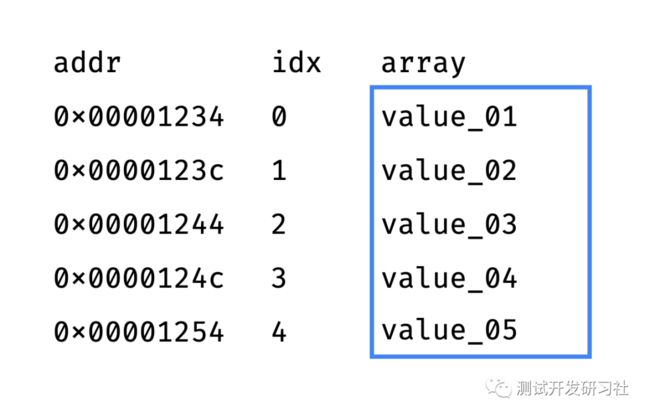
正是由于元素大小相同且连续排列，我们只需要的知道第一个元素（数组的 “头”）的内存地址便可以很容易通过” 索引 “获取数组中的任意一项。

假设头部位于 address 0×00001234，每个元素占用 8 个字节，

则可以根据元素的索引 idx 知道元素地址位于：0×00001234 + idx*8：

由于 “按地址获取值” 内存操作需要固定时间，因此按索引选择数组项也需要 O (1)。

粗略地说，这就是 Python 列表的工作方式：它存储指向数组头部的指针和数组中的项目数。

项目计数是单独存储的，因此该 len() 函数也可以在 O (1) 时间内执行，并且不必每次都对元素进行计数。

到目前为止，一切都很好。但是有几个问题：

• 数组中元素的大小（类型）相同，但列表却能够存储不同大小（类型）的元素

• 数组具有固定长度，但列表的长度随着存储元素的数量动态变化

这看起让人糊涂：究竟该怎么理解列表和数组

我们稍后会解决它们。

2. 复现一个非常原始的列表

掌握数据结构的最好方法是从头开始实现它。

不幸的是，Python 不太适合实现数组这样的低级结构，因为它不支持显式指针（内存中的地址）。

这可能是我们能得到的最接近的：

class OhMyList:    def __init__(self):        self.length = 0        self.capacity = 8        self.array = (self.capacity * ctypes.py_object)() 
    def append(self, item):        self.array[self.length] = item        self.length += 1
    def __len__(self):        return self.length
    def __getitem__(self, idx):        return self.array[idx]

我们的自定义列表具有固定容量（capacity= 8 项）并将元素存储在 array 数组中。

ctypes 模块允许访问标准库所基于的底层结构。在本例中，我们使用它创建一个 C 风格的 “固定容量 “数组。

3. 列表 = 指针数组

该列表立即按索引检索项目，因为它内部有一个数组。数组如此之快，因为所有元素的大小都相同。

但是列表中的元素可以有不同的大小：

guests = ["Frank", "Claire", "Zoe", True, 42]

为了解决这个问题，有人提出了存储项目指针而不是项目值的想法。数组的每个元素都是一个内存地址，如果追随这个地址 —— 你会得到实际的值：

数组紧密相邻地存储这些指针，但是指针引用的值可以存储在内存中的任何位置

由于指针是固定大小的（现代 64 位处理器上为 8 个字节），所以一切正常。我们现在要做两个操作，而不是一个操作（从数组单元格中获取值）：

1. 从数组单元中获取地址。

2. 获取该地址的值。

但它仍然是常数时间 O (1)。

4. 列表 = 动态数组

如果列表下方的数组中有空间，则.append(item) 以恒定时间运行。只需将新值写入空闲单元格并将元素计数器增加 1：​​​​​​​

def append(self, item):    self.array[self.length] = item    self.length += 1

但是如果数组已经满了怎么办？

事实上 Python 必须创建一个更大容量的新数组，并将所有旧项复制到新数组中：

当旧数组中没有更多空间时，是时候创建一个新数组了。

我们开始吧：​​​​​​​

def append(self, item):    if self.length == self.capacity:        self._resize(self.capacity*2)    self.array[self.length] = item    self.length += 1
def _resize(self, new_cap):    new_arr = (new_cap * ctypes.py_object)()    for idx in range(self.length):        new_arr[idx] = self.array[idx]    self.array = new_arr    self.capacity = new_cap

._resize() 是一项昂贵的操作，因此新数组应该比旧数组大得多，以避免频繁操作。

在上面的示例中，新数组的大小是原来的两倍。

事实上 Python 使用了一个更适中的系数 —— 大约 1.12。

如果你通过.pop() 删除列表中超过一半的项目，Python 会缩小它：将分配一个新的、较小的数组并将元素移入其中。

因此，Python 中的列表游刃有余地进行着数组操作

5. 将项目附加到列表

按索引从列表中取值的耗时是 O (1)—— 我们已经解决了这个问题。

用.append(item) 方法加入内容也是 O (1)，直到 Python 必须扩展列表下的数组。

但是数组扩展是一个 O (n) 操作。那么到底.append() 需要多长时间呢？

测量单次 append 是错误的 —— 正如我们发现的那样，有时需要 O (1)，有时需要 O (n)。

所以计算机科学家想出了分摊分析法。要获得分摊的操作时间，可以估计一系列 K 操作将花费的总时间，然后将其除以 K。

在不详细说明的情况下，我会说分摊时间.append(item) 是恒定的 ——O (1)。所以附加到列表中的工作非常快。

为什么分摊附加时间是 O (1)

假设列表为空并且想要追加 n 项目。为简单起见，我们将使用扩展因子 2。让我们计算原子操作的数量：

• 第一项：1（副本）+ 1（插入）

• 另一个 2：2（复制）+ 2（插入）

• 另一个 4：4（复制）+ 4（插入）

• 另一个 8：8（复制）+ 8（插入）

• ...

对于 n 项目将有 n 插入。

至于副本：

​​​​​​​

1 + 2 + 4 + ... log(n) = = 2**log(n) * 2 - 1 == 2n - 1

操作。

所以对于 n 项目会有 3n - 1 原子操作。

O((3n - 1) / n)=O(1)

总结一下，以下操作保证很快：​​​​​​​

# O(1)lst[idx]
# O(1)len(lst)
# amortized O(1)lst.append(item)lst.pop()

6. 总结

我们发现，这些操作是 O (1)：

• 按索引选择数据 lst[idx]

• 统计数据个数 len(lst)

• 从列表末尾追加数据.append(item)

• 从列表末尾删除数据.pop()

其他操作很 “慢”：

• 按索引插入或删除项目，花费线性时间 O (n)，因为它们将所有元素移到目标元素之后。

  • .insert(idx, item)

  • .pop(idx)

• 按值搜索或删除项目，花费线性时间 O (n)，因为它们遍历所有元素。

  • item in lst

  • .index(item)

  • .remove(item)

• 进行 k 个元素的切片，花费时间 O (k)。

  • lst[from:to]

这是否意味着我们不应该使用 “慢” 操作？

当然不是。

对于有 1000 个项目的列表，则单个操作的 O (1) 和 O (n) 之间的差异是微不足道的。

如果你对一个包含 1000 个项目的列表，执行一百万次 “慢” 操作，差异就比较显著了。

或者，对一百万个项目的列表，调用单次 “慢” 操作，也比较显著。

因此，了解哪些列表方法需要恒定时间，以及哪些需要线性时间是很有用的 —— 以便在特定情况下做出有意识的决定。

我希望你能在这篇文章之后以一种新的方式看见 Python 列表。

感谢阅读！

---

欢迎关注我的公众号“ 测试开发研习社”，专注Python开发及测试技术