【java算法笔记】
Java算法笔记
本篇博客为个人在学习过程中的个人总结,从刚开始刷题积累的一些题型,有些可能比较简单,有些复杂,都是我在刷题过程中或者比赛中吃过亏的题型,或者遇到第二次但还是写不出来的题型。希望对您有些启发。持续更新中。
1、求第n行的杨辉三角
快速方法:
//该方法只能从第二行开始,所以i= 1 不是等与0
class Solution {
public List<Integer> getRow(int rowIndex) {
List<Integer> row = new ArrayList<Integer>();
row.add(1);
for (int i = 1; i <= rowIndex; ++i) {
row.add((int) ((long) row.get(i - 1) * (rowIndex - i + 1) / i));
}
return row;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/pascals-triangle-ii/solution/yang-hui-san-jiao-ii-by-leetcode-solutio-shuk/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2、并查集
bilibili讲解:[【算法】并查集(Disjoint Set)共3讲]_哔哩哔哩_bilibili
用途:
①判断是否有环:990. 等式方程的可满足性 - 力扣(LeetCode) (leetcode-cn.com)
class Solution {
public boolean equationsPossible(String[] equations) {
UnionFind unionfind = new UnionFind();
for(String eq : equations){
if(eq.charAt(1) == '='){
int ch1 = (int)(eq.charAt(0) - 'a');
int ch2 = (int)(eq.charAt(3) - 'a');
unionfind.union(ch1, ch2);
}
}
for(String eq : equations){
if(eq.charAt(1) == '!'){
int ch1 = (int)(eq.charAt(0) - 'a');
int ch2 = (int)(eq.charAt(3) - 'a');
if(unionfind.isCollect(ch1, ch2)) return false;
}
}
return true;
}
public class UnionFind{
private int[] parent;
public UnionFind(){
parent = new int[26];
for(int i = 0; i < 26; i ++){
parent[i] = i;
}
}
//如果有连接,则让所有的节点的父节点置为同一个
public void union(int x, int y){
int rootx = find(x);
int rooty = find(y);
if(rootx == rooty) return;
parent[rootx] = rooty;
}
//找出该节点的父节点
public int find(int x){
if(x != parent[x]){
parent[x] = find(parent[x]);
}
return parent[x];
}
//如果两个节点父节点相同,说明相连,此时这两个节点又相连,则会形成环
public boolean isCollect(int x, int y){
int rootx = find(x);
int rooty = find(y);
if(rootx == rooty) return true;
return false;
}
}
}
②判断图是否相连(既有多少个父节点,如果只有一个,则相连,如果有两个以上,说明不相连)
[(41条消息) 蓝桥杯2020] E题.七段码 //dfs+并查集_晚樱-CSDN博客_蓝桥杯七段码
//蓝桥杯
package lanqiao.paper_2020;
public class problem_5 {
static int[] parent = new int[8];
static int[] used = new int[8];
static int[][] e = new int[8][8];
static int ans = 0;
public static void main(String[] args) {
e[1][2]=e[1][6] = 1;
e[2][1]=e[2][7]=e[2][3]=1;
e[3][2]=e[3][4]=e[3][7]=1;
e[4][3]=e[4][5]=1;
e[5][4]=e[5][6]=e[5][7]=1;
e[6][1]=e[6][5]=e[6][7]=1;
e[7][2]=e[7][3]=e[7][5]=e[7][6] = 1;
dfs(1);
System.out.println(ans);
}
public static void dfs(int count){
if(count > 7){
for(int i = 1; i <= 7; i ++) parent[i] = i;
for(int i = 1; i <= 7; i ++){
for(int j = 1; j <= 7; j++){
if(e[i][j] == 1 && used[i] == 1 &&used[j] == 1){ //如果列举的情况中有边是相邻的,让他们的父边相同
if(find(i) != find(j)){ //如果两条边的父边不相同,就将其中一个父边作为另一个父边的父边
parent[find(i)] = find(j);
}
}
}
}
int num = 0;
for(int i = 1; i <= 7; i ++){
if(used[i] == 1 && parent[i] == i){
num ++;
}
}
if(num == 1){
ans ++;
}
return ;
}
//当前值为1
used[count] = 1;
dfs(count+1);
//当前值为0
used[count] = 0;
dfs(count+1);
}
//找出该边的父边
public static int find(int x){
if(parent[x] == x) return x;
x = parent[x];
return find(x);
}
}
例题:
class Solution {
int[] parents;
public int removeStones(int[][] stones) {
parents = new int[20002];
//这里先不初始化每个点的父节点为自己,当用到时初始化,这里先初始化为-1
Arrays.fill(parents, -1);
int n = stones.length;
for(int i = 0; i < n; i ++){
merge(stones[i][0], stones[i][1]+10001);
}
int num = 0;
//如果一个点的父节点是它自己,联通分量的值加一
for(int i = 0; i < 20002; i ++){
if(parents[i] == i) num++;
}
return n - num;
}
public void merge(int x, int y){
int px = find(x);
int py = find(y);
if(px == py) return;
parents[px] = py;
}
public int find(int x){
//第一次用到时初始化
if(parents[x] == -1) parents[x] =x;
if(parents[x] != x){
int px = find(parents[x]);
parents[x] = px;
}
return parents[x];
}
}
3、求解最长公共子序列
利用动态规划:
重点代码:
if(sA[i-1].equals(sB[j-1])) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
import java.util.Scanner;
/*
LanQiaoBei
LanTaiXiaoBei
蓝桥杯历届真题 蓝肽子序列
*/
public class problem_10 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String A = in.nextLine();
String B = in.nextLine();
String[] sA = new String[1000];
int cnt1 = 0;
int b1 = 0;
for(int i=1;i<A.length();i++) {
char now = A.charAt(i);
if(now>='A'&&now<='Z') {
sA[cnt1++]=A.substring(b1,i);
b1 = i;
}
}
sA[cnt1++] = A.substring(b1,A.length());
String[] sB = new String[1000];
int cnt2 = 0;
int b2 = 0;
for(int i=1;i<B.length();i++) {
char now = B.charAt(i);
if(now>='A'&&now<='Z') {
sB[cnt2++]=B.substring(b2,i);
b2 = i;
}
}
sB[cnt2++] = B.substring(b2,B.length());
int[][] dp = new int[cnt1+1][cnt2+1];
for(int i =1; i <= cnt1; i ++){
for(int j = 1; j <= cnt2; j ++){
if(sA[i-1].equals(sB[j-1])) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
System.out.println(dp[cnt1][cnt2]);
}
}
4、快速求质数
题目:快速求低于某个数的所有质数
(42条消息) 可能是求质数最高效的算法_孤岛沉末-CSDN博客_求质数
①试除法:把已经算出的质数,先保存起来,然后用于后续的试除,效率就大大提高了
void init(){
for (int i=2;i<M;i++){
if (pre[i]==0)
prime[++ptot]=pre[i]=i;
for (int j=1;j<=ptot;j++){
int t =i*prime[j];
if (t>=M) //平方超过了
break;
pre[t]=prime[j];
if (i%prime[j]==0)
break;
}
}
}
②筛法:
首先,2是公认最小的质数,所以,先把所有2的倍数去掉;然后剩下的那些大于2的数里面,最小的是3,所以3也是质数;然后把所有3的倍数都去掉,剩下的那些大于3的数里面,最小的是5,所以5也是质数……上述过程不断重复,就可以把某个范围内的合数全都除去(就像被筛子筛掉一样)
int max = n;
int cnt = 0;
int[] p = new int[max+1];
int[] f = new int[max+1];
for(int i=2;i<=max;i++) {
if(f[i]==0) p[cnt++] = i;
for(int j=0;j<cnt&&i*p[j]<=max;j++) {
f[i*p[j]]=1;
//线性筛
//这是因为如果p[j]是i的因数的话,那么p[j]*i的最小质因数只能是p[j],我们的目标是,用每一个合数的最小质因数来删除这个合数,这样就能保证,每个合数都只被删除一次。
if(i%p[j]==0) break;
}
}
5、求两个数的最大公因数
https://leetcode.cn/problems/count-primes/solution/ji-shu-zhi-shu-by-leetcode-solution/
辗转相除法
public static long gcd(long a, long b){
while( a != b){
if(a > b){
a = a - b;
}else{
b = b - a;
}
}
return a;
}
余数法:
计算两个非负整数 p 和 q 的最大公约数:若q 是 0,则最大公约数为 p。否则,将 p 除以q 得到余数 r, p 和 q 的最大公约数即为 q 和r 的最大公约数。
public static int gcd(int p, int q)
{
if (q == 0) return p;
int r = p % q;
return gcd(q, r);
}
6、快速乘&快速幂
适用范围:快速计算a*b % mod的结果(主要目的是换乘法为加法,防止爆数据),或者快速计算a^b % mod 的结果,时间复杂度大大降低。
算法描述:首先你可能会问ab不是直接乘就出来了么,为什么需要快速算法?但是乘法在计算机中处理的时间并不是这么快的,也要拆分为加法来做的。所以快速乘法会更快的计算ab的结果,而且a*b%mod可能还没取模就已经爆long long,但快速乘法却不会。快速幂也是同样的道理。
实现的原理都是基于按照二进制位一步一步乘来避免重复的操作,利用前面的中间结果,从而实现快速的目的。
对于乘数b来说,势必可以拆成2进制,比如110101。有一些位为0,有一些位为1。根据乘法分配律:ab=a(b1+b2+b3+…… )
那么对于a53 = a110101(二进制)= a*(100000+10000+100+1)=a*(1000001+100001+10000+1001+100+11)。
那么设立一个ans=0用于保存答案,每一位让a*=2,在根据b的对应为1看是不是加上此时的a,即可完成快速运算。比如刚才的例子让a=5,运转流程如下。
————————————————
版权声明:本文为CSDN博主「StanleyClinton」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/maxichu/article/details/45459715
#include 7、背包问题
视频讲解:【动态规划】背包问题_哔哩哔哩_bilibili
博客:【动态规划】一次搞定三种背包问题 - 弗兰克的猫 - 博客园 (cnblogs.com)
三个背包问题的定义:
01背包:
有N件物品和一个容量为V的背包,第i件物品消耗的容量为Ci,价值为Wi,求解放入哪些物品可以使得背包中总价值最大。
完全背包:
有N种物品和一个容量为V的背包,每种物品都有无限件可用,第i件物品消耗的容量为Ci,价值为Wi,求解放入哪些物品可以使得背包中总价值最大。
多重背包:
有N种物品和一个容量为V的背包,第i种物品最多有Mi件可用,每件物品消耗的容量为Ci,价值为Wi,求解入哪些物品可以使得背包中总价值最大。
例题:
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int n = nums.length;
int sum = 0;
for(int i = 0; i < n; i ++){
sum += nums[i];
}
int neg = (sum - target) / 2;
if((sum - target) % 2 != 0 || neg < 0) return 0;
int[][] dp = new int[n+1][neg+1];
dp[0][0] = 1;
for(int i = 1; i <= n; i ++){
for(int j = 0; j <= neg; j ++){
if(nums[i-1] > j) dp[i][j] = dp[i-1][j];
else{
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
}
}
}
return dp[n][neg];
}
}
8、前缀树(字典树)
视频讲解:【数据结构 10】Trie|前缀树|字典树_哔哩哔哩_bilibili
题目:实现 Trie (前缀树) - 实现 Trie (前缀树) - 力扣(LeetCode) (leetcode-cn.com)
代码实现:
class Trie {
//子节点列表
Trie[] children;
//结束标志
boolean isEnd;
//初始化前缀树
public Trie() {
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for(int i = 0; i < word.length(); i ++){
int index = (int)(word.charAt(i)-'a');
//如果前缀树的子节点为空,则创建该节点
if(node.children[index] == null){
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = searchPrefix(word);
//如果最后一个节点不为空,且结束标记为true,则表示有该字符串
if(node != null && node.isEnd == true) return true;
return false;
}
public boolean startsWith(String prefix) {
Trie node = searchPrefix(prefix);
//如果节点不为空,表示含有该前缀
if(node != null) return true;
return false;
}
private Trie searchPrefix(String prefix){
Trie node = this;
for(int i = 0; i < prefix.length(); i ++){
int index = (int)(prefix.charAt(i)-'a');
if(node.children[index] == null){
return null;
}
node = node.children[index];
}
return node;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
9、Morris 遍历
反序中序遍历该二叉搜索树
利用 Morris 遍历的方法,可以让空间复杂度:O(1),本质是利用空指针存储下一个访问元素的信息,然后再访问后恢复空指针。
class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
TreeNode node = root;
while (node != null) {
if (node.right == null) {
sum += node.val;
node.val = sum;
node = node.left;
} else {
TreeNode succ = getSuccessor(node);
if (succ.left == null) {
succ.left = node;
node = node.right;
} else {
succ.left = null;
sum += node.val;
node.val = sum;
node = node.left;
}
}
}
return root;
}
public TreeNode getSuccessor(TreeNode node) {
TreeNode succ = node.right;
while (succ.left != null && succ.left != node) {
succ = succ.left;
}
return succ;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/w6cpku/solution/suo-you-da-yu-deng-yu-jie-dian-de-zhi-zh-k02c/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
10、子序列的数目
动态规划 https://leetcode-cn.com/problems/21dk04/
方法:
四步走。
1)根据问题给出二维dp数组定义。
要求s子序列中t的个数。立刻定义dp[i] [j]: s的前i个字符中的t的前j个字符的子序列个数。后续为了方便叙述,dp[i] [j]描述为字符串s_i中t_j的个数。
2)分别令两个维度为0,推测边界。
dp[0][j]表示s_0中t_j的个数。s_0是空字符串,只有当j=0时,才有dp[0][j] = 1,表示s子空串中有一个t子空串,否则dp[0][j] = 0,因为一个空串不可能包含一个非空串。
dp[i][0]表示s_i中t0的个数。t_0是空字符串,显然任何串(包括空串)都含有一个空子串。因此dp[i][0] = 1。
注意到,dp[i][0] = 1实际上已经包含了dp[0][j] = 1的情形。
3)寻找转移方程。
dp[i][j]显然要从dp[i-1][?]递推而来。立即思考dp[i-1][j], dp[i-1][j-1]分别与dp[i][j]的关系。
因为少一个字符,自然而然从当前字符着手。考察si的第i个字符(表为s[i])和tj的第j个字符(表为t[j])的关系。
若s[i] ≠ t[j]:那么s_i中的所有t_j子序列,必不包含s[i],即s_i-1和s_i中tj的数量是一样的,得到该情形的转移方程:
dp[i][j] = dp[i-1][j]
若s[i] = t[j]:假设s_i中的所有t_j子序列中,包含s[i]的有a个,不包含的有b个。s_i中包含s[i]的子序列个数相当于s_i-1中t_j-1的个数,不包含s[i]的子序列个数与上一种情况一样,于是得到该情形的转移方程:
a = dp[i-1][j-1]
b = dp[i-1][j]
dp[i][j] = a + b = dp[i-1][j-1] + dp[i-1][j]
4)空间压缩。
也是固定套路,先从二维数组转两个一维数组(交替滚动),再从两个一维数组转一个一维数组(原地滚动),原地滚动时要注意是否需要逆序。
最后代码:
class Solution {
public int numDistinct(String s, String t) {
int slen = s.length();
int tlen = t.length();
if(tlen > slen) return 0;
int[][] dp = new int[slen+1][tlen+1];
for(int i = 0; i <= slen; i ++ ) dp[i][0] = 1;
for(int i = 1; i <= slen; i ++){
for(int j = 1; j <= tlen; j ++){
if(s.charAt(i-1) == t.charAt(j-1)){
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
}else{
dp[i][j] = dp[i-1][j];
}
}
}
return dp[slen][tlen];
}
}
11、循环小数
这里面有一个数学的小知识即:任意整数除以与这个整数位数相同且全由9组成的数,就能得到一个循环小数。
比如,12是个两位数,除于和它相同位数且都由9组成的数就是 12 / 99。结果就是0.121212…循环小数。其他的位数依次类推。
12、旅行商问题(动态规划)
理解思路:找出一条路经过所有点的最小路径,然后从其中找出一个点返回第一个点,计算总路径最小长度。
关键代码:f数组表示状态为i,且最后一个访问的是j的路径最小值
比如有四个点 , 当i为 1001 表示第一个已经访问,第四个已经访问, f[1001] [4] 表示状态为1001,且最后一个访问的是4号点。
多有转移方程为:f[i] [j] = min(f[i] [j], f[(i-(1< 方法一:分析:通过动态规划来求的时间复杂度为O2,主要代码如下: 方法二:通过一个p[i]来记录长度为i的递增序列中最后一个字符串的下标,从头开始遍历字符串数组a,在p中利用二分法来查找小于a[i]的p[j]的最大值,p是递增的。具体解析: 用一个数组low[i]表示:长度为i的子序列的末端最小值。 同时注意到,对于low的所有元素,low[j+1]>=low[j]恒成立 那么什么时候low[j+1]会更新:当a[i]>a[j]且a[i] 代码: 传统的基于比较的排序算法(快速排序、归并排序等)均需要 O(N\log N)O(NlogN) 的时间复杂度。 线性时间的排序:基数排序,桶排序 自定义排序: 例题:https://leetcode.cn/problems/course-schedule-ii/ BFS: 们使用一个队列来进行广度优先搜索。开始时,所有入度为 00 的节点都被放入队列中,它们就是可以作为拓扑排序最前面的节点,并且它们之间的相对顺序是无关紧要的。 在广度优先搜索的每一步中,我们取出队首的节点 uu: 我们将 uu 放入答案中; 我们移除 uu 的所有出边,也就是将 uu 的所有相邻节点的入度减少 11。如果某个相邻节点 vv 的入度变为 00,那么我们就将 vv 放入队列中。 在广度优先搜索的过程结束后。如果答案中包含了这 nn 个节点,那么我们就找到了一种拓扑排序,否则说明图中存在环,也就不存在拓扑排序了。 DFS: 我们将当前搜索的节点 uu 标记为「搜索中」,遍历该节点的每一个相邻节点 vv: 如果 vv 为「未搜索」,那么我们开始搜索 vv,待搜索完成回溯到 uu; 如果 vv 为「搜索中」,那么我们就找到了图中的一个环,因此是不存在拓扑排序的; 如果 vv 为「已完成」,那么说明 vv 已经在栈中了,而 uu 还不在栈中,因此 uu 无论何时入栈都不会影响到 (u, v)(u,v) 之前的拓扑关系,以及不用进行任何操作。 方法一:利用额外空间 方法二:反转数组 对于有序数组,两个值的和为target,让left = 0, right = n-1,if nums[left] + nums[right] < target - > left ++ if nums[left] + nums[right] > target -> right --; 知道找到和为target的两个数。 超级详细:https://leetcode.cn/circle/discuss/ooxfo8/ 最终位置 right left, 如果存在mid和pos相等,left 的位置为值的位置。 例题:https://leetcode.cn/problems/kth-smallest-number-in-multiplication-table/ 利用C[ n ] [ m ] = C(n-1, m - 1) + C(n-1,m)计算C[ n ] [ m ] 数组 (转化为二分图最大匹配问题) 做到蓝桥杯题目《估计人数》时查找答案时发现,这是一类非常经典的问题,可相交的最小路径覆盖。 题目链接:http://lx.lanqiao.cn/problem.page?gpid=T2741 解题链接:https://blog.csdn.net/qq_43319748/article/details/109679073 解题思路:https://www.cnblogs.com/ka200812/archive/2011/07/31/2122641.html 首先,最小路径覆盖=总节点数-最大匹配数。这个应该已经是路人皆知了。 所谓最小路径覆盖,是指在一个有向图中,找出最少的几条路径,用它们来覆盖全图 这里说的值得注意的地方,如果有向图的边有相交的情况,那么就不能简单的对原图求二分匹配了 举个例子,假设有图:1->2 2->5 2->3 4->2,事实上,这其实就是两条边:1->5 4->3 ,节点2只是他们的一个交点 如果只是简单的在原图的基础上求二分匹配,那么得到的匹配答案是2,最小路径覆盖答案便是5-2=3。 可是随便一看都能看看出端倪,这个图中,只需要两个点便可以探索完整个地图,这里最小路径覆盖数明显是2。 问题究竟出在哪里呢?其实就和这个交点2有关。既然边有相交,那么他们的连通性也应该连通下去。 解决的办法是对原图进行一次闭包传递(也就是flody),于是便增加了四条边:1->3 1->5 4->3 4->5 这时再求最大匹配数,匹配答案便是3,最小路径覆盖值为2,这是正确答案! 其中涉及到最小路径覆盖, 会用到弗洛伊德算法和匈牙利算法: 1、 “可相交的最小路径覆盖” 和“不相交的最小路径覆盖”的概念:https://blog.csdn.net/qq_39627843/article/details/82012572 2:、弗洛伊德算法:https://www.cnblogs.com/wangyuliang/p/9216365.html 3、匈牙利算法:https://blog.csdn.net/Arabic1666/article/details/79824390 基础代码讲解:https://zhuanlan.zhihu.com/p/106118909 例题:https://blog.csdn.net/weixin_42638946/article/details/115512941 leetcode入门题目:https://leetcode.cn/problems/range-sum-query-mutable/ 代码: 代码讲解:https://blog.csdn.net/qq_40941722/article/details/104406126 LeetCode例题:https://leetcode.cn/problems/range-sum-query-mutable/ 思路二:动态规划。维护前k个数,并维护 第k个数由哪个数乘于3,5, 7得来,维护3个指针,分别表示前k个数中的最小3,5,7倍数。 通过PriorityQueue找数据流中的中位数 LinkedList:LinkedList类实现了List接口和Collection接口,是List接口的链接列表实现。允许所有元素(包括 null)。这些操作允许将链接列表用作堆栈、队列或双端队列。此类提供队列操作,以及其他堆栈和双端队列操作。所有操作都是按照双重链接列表的需要执行的。在列表中编索引的操作将从开头或结尾遍历列表(从靠近指定索引的一端)。 遍历: 遍历:https://blog.csdn.net/leijie0322/article/details/123023309 例题:https://leetcode.cn/problems/top-k-frequent-elements/ int num = entry.getKey(), count = entry.getValue();for(int i = 0; i < 1 << n; i ++){
for(int j = 0; j < n; j ++){
//选出一个为1的位作为最后一个点
if(((i >> j) & 1) == 1){
for(int k = 0; k < n; k ++){
//选出一个由第k位为1的点, 这个点为上一步到最后一位为j的点
if((((i-(1<<j)) >> k) & 1) == 1 ){
f[i][j] = Math.min(f[i][j], f[(i-(1<<j))][k]+w[k][j]);
}
}
}
}
}
import java.text.DecimalFormat;
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int D = scanner.nextInt();
int[][] pos = new int[n][2];
for(int i = 0; i < n; i ++){
pos[i][0] = scanner.nextInt();
pos[i][1] = scanner.nextInt();
}
double[][] w = new double[n][n];
double[][] f = new double[1<<n][n];
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j ++){
double td = Math.sqrt(Math.pow(pos[i][0]-pos[j][0] ,2)+ Math.pow(pos[i][1]-pos[j][1],2));
if(td > D){
w[i][j] = w[j][i] = Integer.MAX_VALUE;
}else{
w[i][j] = w[j][i] = td;
}
}
}
for (int k = 0; k < n; k ++){
for (int i = 0; i < n; i ++){
for (int j = 0; j < n; j ++){
w[i][j] = Math.min(w[i][j], w[i][k] + w[k][j]);
}
}
}
for (int i = 0; i < 1 << n; i ++){
for (int j = 0; j < n; j ++){
f[i][j] = Integer.MAX_VALUE;
}
}
f[1][0] = 0;
for(int i = 0; i < 1 << n; i ++){
for(int j = 0; j < n; j ++){
if(((i >> j) & 1) == 1){
for(int k = 0; k < n; k ++){
if((((i-(1<<j)) >> k) & 1) == 1 ){
f[i][j] = Math.min(f[i][j], f[(i-(1<<j))][k]+w[k][j]);
}
}
}
}
}
double ans = Integer.MAX_VALUE;
for(int i = 1; i < n; i ++){
ans = Math.min(ans, f[(1<<n)-1][i]+w[i][0]);
}
DecimalFormat df = new DecimalFormat("0.00");
ans = Math.round(ans * 100.0) * 1.0 / 100;
System.out.println(df.format(ans));
}
}
13、最长递增子序列
//dp[i][0]用来记录每个字符串作为最后一个字符串的最大个数,dp[i][1]记录前一个字符串的位置,方便后面回溯 。
for(int i = 0; i < size; i ++){
int max = 0;
int index = i;
for(int j = 0; j < i; j ++){
if(dp[j][0] > max && strList.get(i).compareTo(strList.get(j)) > 0){
max = dp[j][0];
index = j;
}
}
dp[i][0] = max + 1;
dp[i][1] = index;
if(dp[i][0] > finalmax){
finalmax = dp[i][0];
finalindex = i;
}
}
遍历每一个a[i]时找到一个j,如果low[j]
我们看low[j+1]是否比a[i]大如果low[j+1]>a[i]那么low[j+1]=a[i](显然)
就是说长度为j+1的子序列的最后一个元素值一定大于j的子序列的最后一个元素值
这是因为长度为j+1的子序列就包括长度为j的子序列
即C++里的lower_bound(序列中的第一个大于等于target的位置)
如果求的不是最长上升子序列而是最长不下降子序列的话就用upper_bound了
因为此时的条件是a[i]>=a[j]且a[i]import java.util.Scanner;
public class test10_2 {
public static int N = 1000010;
public static String[] a = new String[N];
public static int size = 0;
public static int[] p = new int[N];
public static int[] pre = new int[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String str = scanner.next();
int slen = str.length();
for(int i = 0; i < slen; i++){
for(int j = i+1; j <= slen; j ++ ){
if(j < slen && str.charAt(j) <= 'Z'){
a[++size] = str.substring(i,j);
i = j-1;
break;
}else if(j == slen){
a[++size] = str.substring(i,j);
i = j;
break;
}
}
}
//len的值是动态增加的,如果a[i]的值比p[i]为下标的所有的值都大,则len+1
int len = 0;
for(int i = 1; i <= size; i ++){
int l = 0, r = len;
//二分法,查找a[i]在p[i]中的位置
while(l < r){
int mid = (l + r + 1 ) >> 1;
if(a[p[mid]].compareTo(a[i]) < 0) l = mid;
else r = mid-1;
}
//修改p[r+1]的值
p[r + 1] = i;
pre[i] = p[r];
len = Math.max(len, r + 1);
}
//回溯
int index = p[len];
StringBuilder ans = new StringBuilder();
while(index != 0){
ans.insert(0, a[index]);
index = pre[index];
}
System.out.println(ans);
}
}
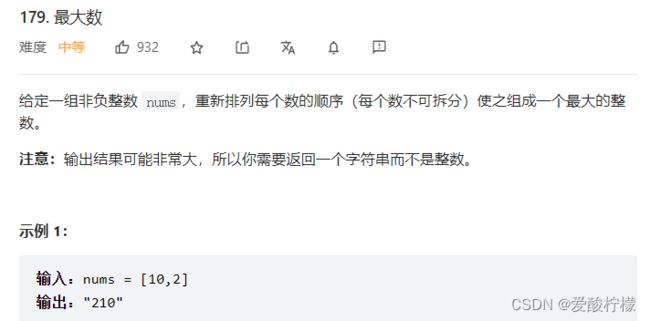
14、排序
class Solution {
public String largestNumber(int[] nums) {
//将数组换为包装类
Integer[] nums2 = new Integer[nums.length];
for(int i = 0; i < nums.length; i ++){
nums2[i] = nums[i];
}
Arrays.sort(nums2, new Comparator<Integer>(){
public int compare(Integer a, Integer b){
String sa = String.valueOf(a);
String sb = String.valueOf(b);
Long val1 = Long.parseLong(sa + sb);
Long val2 = Long.parseLong(sb + sa);
if(val1 > val2) return -1;
return 1;
}
});
//lambda表达式
// Arrays.sort(nums2, (a, b)->{
// String sa = String.valueOf(a);
// String sb = String.valueOf(b);
// Long val1 = Long.parseLong(sa + sb);
// Long val2 = Long.parseLong(sb + sa);
// if(val1 > val2) return -1;
// return 1;
// });
StringBuilder ans = new StringBuilder();
if (nums2[0] == 0) {
return "0";
}
for( int i = 0; i < nums2.length; i ++ ){
ans.append(""+nums2[i]);
}
String str = ans.toString();
return str.length() == 0 ? "0": str;
}
}
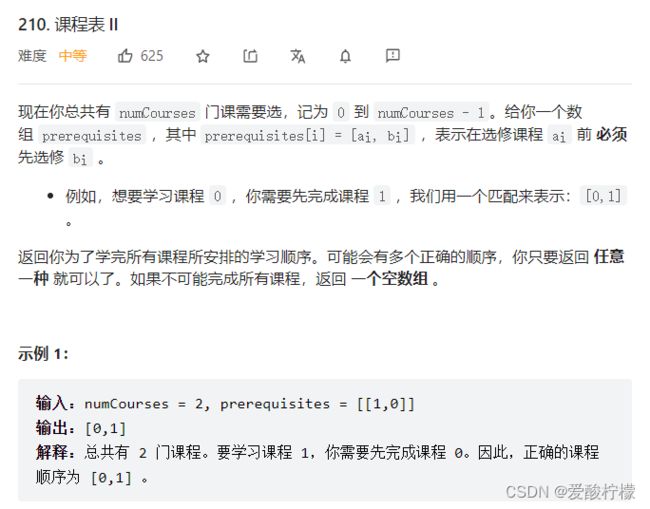
15、拓扑排序
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<List<Integer>> edges = new ArrayList<List<Integer>>();
for(int i = 0; i < numCourses; i ++){
edges.add(new ArrayList<Integer>());
}
int[] indexg = new int[numCourses];
for(int i = 0; i < prerequisites.length;i++){
edges.get(prerequisites[i][1]).add(prerequisites[i][0]);
indexg[prerequisites[i][0]] ++;
}
Deque<Integer> queue = new LinkedList<Integer>();
for(int i = 0;i < numCourses; i ++){
if(indexg[i] == 0){
queue.addLast(i);
}
}
int[] ans = new int[numCourses];
int index = 0;
while(!queue.isEmpty()){
int tv = queue.removeFirst();
ans[index++] = tv;
for(int v: edges.get(tv)){
indexg[v] --;
if(indexg[v] == 0) queue.addLast(v);
}
}
if(index < numCourses) return new int[]{};
return ans;
}
}
class Solution {
// 存储有向图
List<List<Integer>> edges;
// 标记每个节点的状态:0=未搜索,1=搜索中,2=已完成
int[] visited;
// 用数组来模拟栈,下标 n-1 为栈底,0 为栈顶
int[] result;
// 判断有向图中是否有环
boolean valid = true;
// 栈下标
int index;
public int[] findOrder(int numCourses, int[][] prerequisites) {
edges = new ArrayList<List<Integer>>();
for (int i = 0; i < numCourses; ++i) {
edges.add(new ArrayList<Integer>());
}
visited = new int[numCourses];
result = new int[numCourses];
index = numCourses - 1;
for (int[] info : prerequisites) {
edges.get(info[1]).add(info[0]);
}
// 每次挑选一个「未搜索」的节点,开始进行深度优先搜索
for (int i = 0; i < numCourses && valid; ++i) {
if (visited[i] == 0) {
dfs(i);
}
}
if (!valid) {
return new int[0];
}
// 如果没有环,那么就有拓扑排序
return result;
}
public void dfs(int u) {
// 将节点标记为「搜索中」
visited[u] = 1;
// 搜索其相邻节点
// 只要发现有环,立刻停止搜索
for (int v: edges.get(u)) {
// 如果「未搜索」那么搜索相邻节点
if (visited[v] == 0) {
dfs(v);
if (!valid) {
return;
}
}
// 如果「搜索中」说明找到了环
else if (visited[v] == 1) {
valid = false;
return;
}
}
// 将节点标记为「已完成」
visited[u] = 2;
// 将节点入栈
result[index--] = u;
}
}
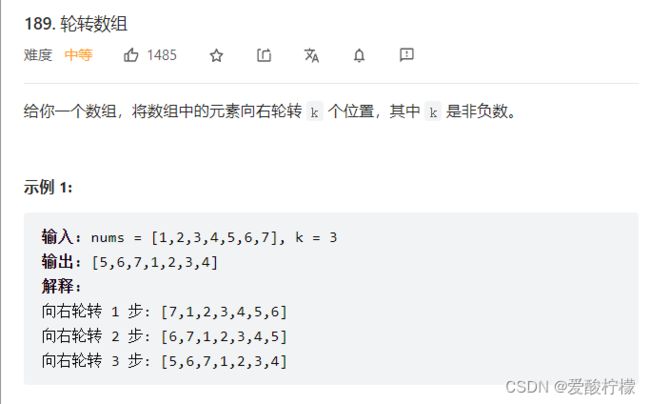
16、轮转数组
class Solution {
public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
public void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start += 1;
end -= 1;
}
}
}
17、双指针
18、二分查找
其中一种:
int left = 1, right = N-1;
while(left <= right){
int mid = left + (right - left) / 2;
if(col[mid] < pos)
left = mid+1;
else{
right = mid-1;
}
}
class Solution {
public int findKthNumber(int m, int n, int k) {
int left = 1, right = m * n;
while(left < right){
int mid = left + (right-left) / 2;
int count = mid / n * n;
for(int i = mid / n + 1; i <= m; i ++){
count += mid / i;
}
if(count >= k){
right = mid;
}else {
left = mid + 1;
}
}
return left;
}
}
19、组合数学Cnm的计算
package lanqiao_final._12;
import java.util.Scanner;
public class test6 {
public static long[][] C = new long[65][65];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
long N = scanner.nextLong();
int K = scanner.nextInt();
long ans = 0;
for(int k = 63; k >=0; k --){
if((N >>k & 1) == 1){
ans += C(k, K--);
if(K == 0){
ans ++;
break;
}
}
}
System.out.println(ans);
}
public static long C(int n, int m){
if(m > n) return 0;
if(n == 0 || m == 0 || n == m) return 1;
if(C[n][m] != 0) return C[n][m];
return C[n][m] = C(n-1, m - 1) + C(n-1,m);
}
}
20、计算三角函数
double r = random.nextDouble() * radius;
double angle = random.nextDouble() * 360;
double[] ans = new double[2];
ans[0] = x_center + r * Math.cos(Math.toRadians(angle));
ans[1] = y_center + r * Math.sin(Math.toRadians(angle));
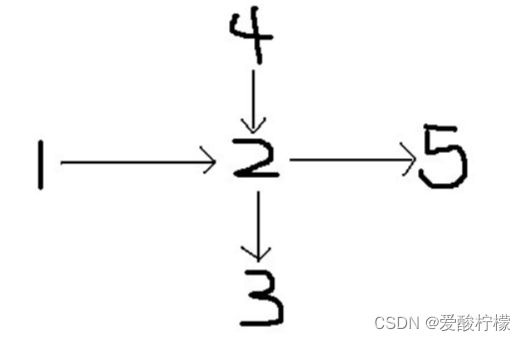
21、可相交的最小路径覆盖
import java.util.Scanner;
public class Main {
/* 可相交的最小路径覆盖 */
// n行m列
int n, m;
//地图
char[][] matrix;
//地图有多少个可以走的点
int pointcount = 0;
//连接表,记录每个点到任意一个点是否走到,构成一个二维矩阵
boolean[][] con;
//给每一个点标上序号,第一个点序号为1,跟地图位置对应
//功能:作为索引用于转换 连接表con
int[][] num;
/* 匈牙利算法的工具 */
//匹配表,存放匹配关系,如:一个点a匹配另一个点b,但b有被其他点匹配过,都在这个表中对应
int[] matchtable;
//点b是否被匹配过
boolean[] ismatch;
public Main() {
Scanner sn = new Scanner(System.in);
n = sn.nextInt();
m = sn.nextInt();
matrix = new char[n][m];
num=new int[n][m];
sn.nextLine();
//读取地图
for (int i = 0; i < n; i++) {
matrix[i] = sn.nextLine().trim().toCharArray();
for (int j = 0; j < m; j++) {
//记录序号,从1开始的
if (matrix[i][j] == '1')num[i][j]=++pointcount;
}
}
//设置连接表大小,0位置不能用,因此需要pointcount+1的行和列
con=new boolean[pointcount+1][pointcount+1];
//根据序号开始转换连接表
for(int i=0;i<n-1;i++){
for(int j=0;j<m-1;j++){
//如果可以向下走或者向右走,说明两个点之间存在直接连接关系,对应到con上
if(matrix[i][j]=='1'&&matrix[i][j+1]=='1')
con[num[i][j]][num[i][j+1]]=true;
if(matrix[i][j]=='1'&&matrix[i+1][j]=='1')
con[num[i][j]][num[i+1][j]]=true;
}
}
/* 弗洛伊德算法 */
/* 以k为中间点,遍历所有点是否能够使得con表中原本不能直接相连的点a和点b
* 但通过k点,可以将a和b连接起来。
* 比如k在a的右边,b在k的下边,那通过k就可以使得a,b连接
*/
for(int k=1;k<=pointcount;k++){
for(int i=1;i<=pointcount;i++){
for(int j=1;j<=pointcount;j++){
con[i][j]|=(con[i][k]&&con[k][j]);
}
}
}
/* 匈牙利算法 */
//开始统计匹配度
//初始化工具
matchtable=new int[pointcount+1];
int count=0;
//统计匹配度
//查看有哪些点可以匹配
for(int i=1;i<=pointcount;i++) {
ismatch=new boolean[pointcount+1];//每次都初始化一次, 这一步很重要,假设让每个节点都没用被访问
if(dfs(i)) count++;
}
//最小路径覆盖=原图的结点数- 所有点根据con找到的最大匹配数
System.out.println(pointcount-count);
}
/* 匈牙利算法核心 */
//点a是否能够匹配到一个合适的点b,
//判断标准就是con中两个点是否能连接
//一个点可能会有很多个点连接
//匈奴利亚算法的功能就是达到最大匹配度
public boolean dfs(int i) {
for(int j=1;j<=pointcount;j++) {
if(!con[i][j])continue;//i和j无连接,跳过
if(!ismatch[j]) {
ismatch[j]=true;
/* 如果在点i之前没有点与点j匹配,直接返回true,匹配成功
* 如果点j已有匹配的点k,
* 但点k还能找到其他点匹配。
* 那就赶走k点,取而代之,将点i与点j匹配
* 点k继续上述过程。
* 如果k的结果返回true。点k找到新的,说明点i可以与点j匹配,匹配成功
* 如果k的结果返回false,说明点i挤走点k,点k无法找到可以匹配的其他点
* 那对我们来说,匹配度是不变的,直接结束,不让i代替k。
*/
if(matchtable[j]==0||dfs(matchtable[j])) {
matchtable[j]=i;
return true;
}
}
}
return false;
}
public static void main(String[] args) {
new Main();
}
}
22、线段树
class NumArray {
int[] arr;
int[] tree;
int n;
public NumArray(int[] nums) {
n = nums.length;
arr = nums;
tree = new int[4*n]; //tree要以1开始,子节点分别为2*p, 2*p+1
build(0, n-1, 1);
}
public void build(int l, int r, int p){
if(l == r){
tree[p] = arr[l];
return;
}
int mid = l + (r - l) / 2;
build(l, mid, 2*p);
build(mid+1, r, 2*p+1);
tree[p] = tree[2*p] + tree[2*p+1];
}
public void update(int index, int val) {
update(index, val, 0, n-1, 1);
}
public void update(int index, int val, int l, int r, int p){
if(l > index || r < index ){
return;
}else if(l == index && r == index){ //确定在同一个区间,没有交叉
tree[p] = val;
} else { //确定会分布在两个区间
int mid = l + (r - l ) / 2;
update(index, val, l, mid, 2*p);
update(index, val, mid+1, r, 2*p + 1);
tree[p] = tree[2*p] + tree[2 * p + 1];
}
}
public int sumRange(int left, int right) {
return query(left, right, 0, n-1, 1);
}
public int query(int cl, int cr, int l, int r , int p){
if(cl > r || cr < l){
return 0;
}else if(l >= cl && r <= cr){
return tree[p];
}else{
int mid = l + (r - l ) / 2;
return query(cl, cr, l, mid, 2 * p) + query(cl, cr, mid + 1, r, 2 * p +1);
}
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* obj.update(index,val);
* int param_2 = obj.sumRange(left,right);
*/
23、树状数组
class NumArray {
int[] nums;
int n;
int[] tree;
public NumArray(int[] nums) {
n = nums.length;
this.nums = nums;
tree = new int[n+1];
for(int i = 0; i < n; i ++){
add(i+1, nums[i]);
}
}
public void update(int index, int val) {
add(index+1, val - nums[index]);
nums[index] = val;
}
public int sumRange(int left, int right) {
return prefixSum(right+1) - prefixSum(left);
}
public int lowbit(int m){
return m & (-m);
}
public void add(int index, int val) {
while(index <= n){
tree[index] += val;
index += lowbit(index);
}
}
public int prefixSum(int index){
int sum = 0;
while(index > 0){
sum += tree[index];
index -= lowbit(index);
}
return sum;
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* obj.update(index,val);
* int param_2 = obj.sumRange(left,right);
*/
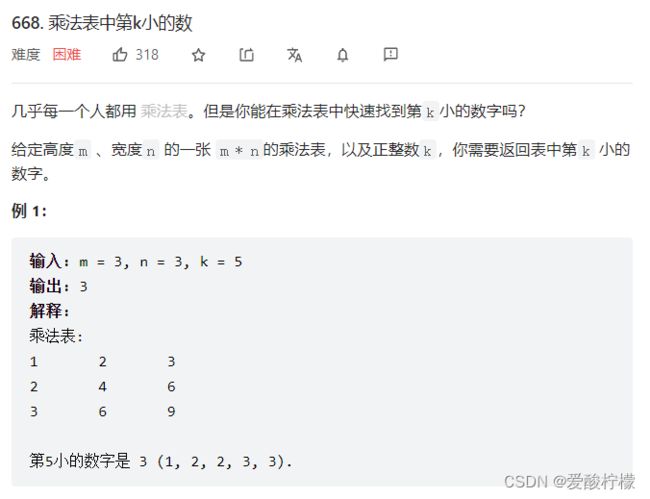
24、第 k 个数
题目链接:https://leetcode.cn/problems/get-kth-magic-number-lcci/
求3,5, 7的倍数构成的数列的第k个数
思路一:维护3,5, 7的倍数列表最小堆,每次取出堆中的最小值,然后再把最小值的3,5,7倍加入到队列。
class Solution {
public int getKthMagicNumber(int k) {
int[] factors = {3, 5, 7};
Set<Long> seen = new HashSet<Long>();
PriorityQueue<Long> heap = new PriorityQueue<Long>();
seen.add(1L);
heap.offer(1L);
int magic = 0;
for (int i = 0; i < k; i++) {
long curr = heap.poll();
magic = (int) curr;
for (int factor : factors) {
long next = curr * factor;
if (seen.add(next)) {
heap.offer(next);
}
}
}
return magic;
}
}
class Solution {
public int getKthMagicNumber(int k) {
int[] factors = {3, 5, 7};
Set<Long> seen = new HashSet<Long>();
PriorityQueue<Long> heap = new PriorityQueue<Long>();
seen.add(1L);
heap.offer(1L);
int magic = 0;
for (int i = 0; i < k; i++) {
long curr = heap.poll();
magic = (int) curr;
for (int factor : factors) {
long next = curr * factor;
if (seen.add(next)) {
heap.offer(next);
}
}
}
return magic;
}
}
java基础数据结构
1、PriorityQueue
自定义比较逻辑,默认是小根堆
maxQueue = new PriorityQueue<Integer>((a,b)->(b-a));
方法:maxQueue.peek(),maxQueue.poll(),minQueue.offer(),maxQueue.size()
遍历:for (Event e : pq)
class MedianFinder {
PriorityQueue<Integer> minQueue;
PriorityQueue<Integer> maxQueue;
int size = 0;
public MedianFinder() {
minQueue = new PriorityQueue<Integer>((a,b)->(a-b));
maxQueue = new PriorityQueue<Integer>((a,b)->(b-a));
}
public void addNum(int num) {
size++;
if(maxQueue.size() == 0 || num <= maxQueue.peek()){
maxQueue.offer(num);
if(maxQueue.size() > minQueue.size() + 1 ){
minQueue.offer(maxQueue.poll());
}
}else{
minQueue.offer(num);
if(minQueue.size() > maxQueue.size()){
maxQueue.offer(minQueue.poll());
}
}
}
public double findMedian() {
if(size % 2 == 0){
return (minQueue.peek() + maxQueue.peek()) * 1.0 / 2;
}else{
return maxQueue.peek();
}
}
}
2、LinkedList
特有方法:
void addFirst(E e) 将指定元素插入此列表的开头。
void addLast(E e) 将指定元素添加到此列表的结尾。
boolean offer(E e) 将指定元素添加到此列表的末尾(最后一个元素)。
boolean offerFirst(E e) 在此列表的开头插入指定的元素。
boolean offerLast(E e) 在此列表末尾插入指定的元素。
E element() 获取但不移除此列表的头元素。
E getFirst() 返回此列表的第一个元素。
E getLast() 返回此列表的最后一个元素。
E poll() 获取并移除此列表的头元素(第一个元素)
E pollFirst() 获取并移除此列表的第一个元素;如果此列表为空,则返回 null
E pollLast() 获取并移除此列表的最后一个元素;如果此列表为空,则返回 null。
int lastIndexOf(Object o) 返回此列表中最后出现的指定元素的索引,如果此列表中不包含该元素,则返回 -1。
int indexOf(Object o)返回此列表中首次出现的指定元素的索引,如果此列表中不包含该元素,则返回 -1。
E pop() 从此列表所表示的堆栈处弹出一个元素。即返回并且移除这个元素
void push(E e) 将元素推入此列表所表示的堆栈
E set(int index, E element)
E add(int index, E element)
Iterator it = LinkedList.iterator()
iterator.add(e) //在开头插入元素
while (iterator.hasNext()) {
String next = iterator.next();
if(next.equals("孙悟空")){
iterator.add(e) ;
iterator.remove("孙悟空");
}
}
3、TreeMap
TreeMap<Integer, String> pairs = new TreeMap<>();
pairs.put(2, "B");
pairs.put(1, "A");
pairs.put(3, "C");
String value = pairs.get(3); //get method
System.out.println(value);
value = pairs.getOrDefault(5, "oops"); //getOrDefault method
System.out.println(value);
//Iteration example
Iterator<Integer> iterator = pairs.keySet().iterator();
while(iterator.hasNext()) {
Integer key = iterator.next();
System.out.println("Key: " + key + ", Value: " + pairs.get(key));
}
//Remove example
pairs.remove(3);
System.out.println(pairs);
System.out.println(pairs.containsKey(1)); //containsKey method
System.out.println(pairs.containsValue("B")); //containsValue method
System.out.println(pairs.ceilingKey(2));
4、TreeSet
Set<String> set = new TreeSet<>();
//添加元素
set.add("c");
set.add("a");
set.add("b");
set.add("a");
//迭代器遍历
Iterator<Integer> it = treeSetObj.iterator();
while (it.hasNext()) {
System.out.println(it.next());
}
//for-each 循环遍历
for(String str : treeSetObj) {
System.out.println(str);
}
5、StringBuilder
StringBuilder sb = new StringBuilder();
sb.append(val); //val可以是字符或者字符串
sb.insert(index, val)
sb.deleteCharAt(index)
sb.delete(startIndex, endIndex)
6、HashMap
class Solution {
public int[] topKFrequent(int[] nums, int k) {
int n = nums.length;
PriorityQueue<int[]> queue = new PriorityQueue<int[]>((a, b)->{
return a[1] - b[1];
});
Map<Integer, Integer> map = new HashMap<Integer,Integer>();
for(int i = 0; i < n; i ++){
map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
}
Iterator<Map.Entry<Integer,Integer>> it = map.entrySet().iterator();
while(it.hasNext()){
Map.Entry<Integer,Integer> entry = it.next();
queue.offer(new int[]{entry.getKey(), entry.getValue()});
if(queue.size() > k) queue.poll();
}
int[] ans = new int[k];
for(int i = 0; i < k; i ++){
ans[i] = queue.poll()[0];
}
return ans;
}
}
for循环:
for (Map.Entry<Integer, Integer> entry : occurrences.entrySet()) {
int num = entry.getKey(), count = entry.getValue();
if (queue.size() == k) {
if (queue.peek()[1] < count) {
queue.poll();
queue.offer(new int[]{num, count});
}
} else {
queue.offer(new int[]{num, count});
}
}
第二种,遍历HashMap的keySet集合,通过HashMap.keySet()得到key集合,通过迭代器Iterator遍历集合得到key和value。
private static void second(Map<Object, Object> map) {
Iterator<Object> iterator = map.keySet().iterator();
while (iterator.hasNext()) {
Object key = iterator.next();
System.out.println("key:" + key + ",vaule:" + map.get(key));
}
}
第三种,遍历HashMap的values集合,通过HashMap.values()得到value集合,通过迭代器Iterator遍历集合得到key和value。
private static void third(Map<Object, Object> map) {
Iterator<Object> iterator = map.values().iterator();
while (iterator.hasNext()) {
Object value = iterator.next();
System.out.println("vaule:" + value);
}
}
7、Stack
class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
Deque<Integer> stack = new LinkedList<Integer>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.isEmpty()) {
stack.push(i);
} else {
maxans = Math.max(maxans, i - stack.peek());
}
}
}
return maxans;
}
}
if (queue.size() == k) {
if (queue.peek()[1] < count) {
queue.poll();
queue.offer(new int[]{num, count});
}
} else {
queue.offer(new int[]{num, count});
}
}
第二种,遍历HashMap的keySet集合,通过HashMap.keySet()得到key集合,通过迭代器Iterator遍历集合得到key和value。
private static void second(Map
Iterator iterator = map.keySet().iterator();
while (iterator.hasNext()) {
Object key = iterator.next();
System.out.println(“key:” + key + “,vaule:” + map.get(key));
}
}
第三种,遍历HashMap的values集合,通过HashMap.values()得到value集合,通过迭代器Iterator遍历集合得到key和value。
private static void third(Map
Iterator iterator = map.values().iterator();
while (iterator.hasNext()) {
Object value = iterator.next();
System.out.println(“vaule:” + value);
}
}
### 7、Stack
```java
class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
Deque