eigen库安装_快速入门矩阵运算——开源库Eigen

矩阵是数学中一个重要的工具，广泛应用于各种场景下的数值分析，例如，数字信号处理，图像处理等。我们如何在程序中使用矩阵进行运算呢？本文将为大家介绍一个开源的矩阵运算工具——Eigen。

Eigen is a C++ template library for linear algebra: matrices, vectors, numerical solvers, and related algorithms.

Eigen是一个用于线性运算的C++ 模板库，支持 矩阵和矢量运算，数值分析及其相关的算法。

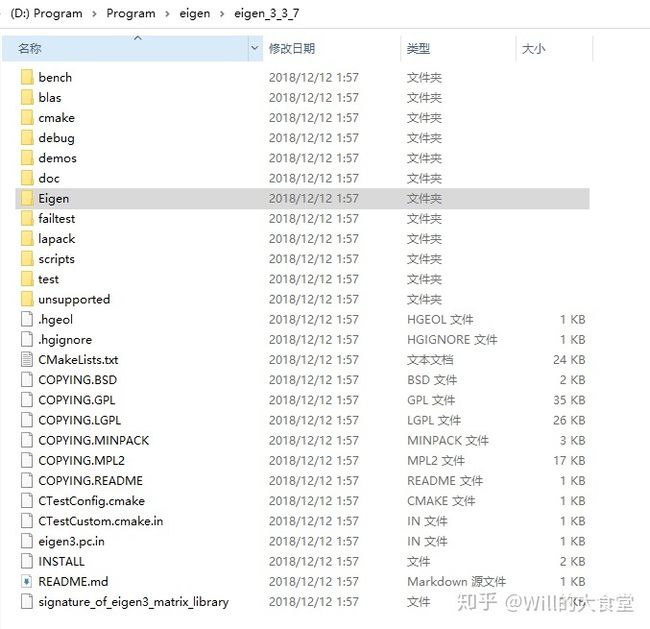
安装Eigen比较简单需要，从官网下载源码并解压即可，我现在的是最新的eigen-3.3.7版本。

官网下载地址：

Eigen​eigen.tuxfamily.org

我们可以进入Eigen目录，可以发现Eigen库主要包括如下几个模块组成：

• Core：Matrix和Array类，基础的线性代数运算和数组操作；
• Geometry：旋转，平移，缩放，2维和3维的各种变换；
• LU：求逆，行列式，LU分解；
• Cholesky：LLT和LDLT Cholesky分解；
• Householder：Householder变换；
• SVD：SVD分解；
• QR：QR分解。
• Eigenvalues：特征值，特征向量分解。
• Sparse：稀疏矩阵的存储和运算。
• Dense：包含了Core、Geometry、LU、Cholesky、SVD、QR、Eigenvalues等模块。
• Eigen：包含了Dense和Sparse模块。

Eigen的食用方法非常之简单，在使用时我们只需要从解压后的文件目录中找到需要使用的库，然后，在源代码中包含相应的库即可食用了。因为Eigen是用模板写的模板库，所以只能把头文件包含进来使用。W君是在工程工作目录解压的，请参考如下代码包含Eigen库。

 #include "eigen_3_3_7/Eigen/Eigen"

Matrix和Array模板类

Eigen库提供有Matrix和Array两种模板类。它们定义如下：

typedef Matrix MyMatrixType;
typedef Array MyArrayType

其中，通常我们会根据需要设置前三个参数，其它为默认值即可。

• Scalar：指定元素类型，比如，float, double, bool, int 等。
• RowsAtCompileTime：指定行数或者设置成动态（Dynamic）；
• ColsAtCompileTime：指定列数或者设置成动态（Dynamic）；
• Options：标志位，可以是ColMajor或RowMajor，默认是ColMajor；

从上面可以看出，行数和列数是允许固定大小，也允许动态大小的，所以下面的几种类型是可以的。

Matrix
Matrix
Matrix
Matrix
Array
Array

另外，我们还可以使用Eigen库已经重定义的类型，下面是一些简单的例子可参考。

矩阵的定义和初始化

下面我们先看看Matrix模板类，它包含矩阵（Matrix）和向量（Vector），对于Vector来说，它也是一个矩阵，不过特殊的是行或者列数为1，我们称作行向量或者列向量。接下来我们来写个程序来看一下。

#include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{
    Eigen::MatrixXf matrix1(3,4); //定义了矩阵的大小，但是没有初始化。
    Eigen::Vector3f vector1;

    matrix1 = Eigen::MatrixXf::Zero(3,4); //对矩阵进行初始化。
    vector1 = Eigen::Vector3f::Ones();

    std::cout << "------ matrix1 ------" << std::endl << matrix1 << std::endl;
    std::cout << "------ vector1 ------" << std::endl << vector1 << std::endl;
}

在上面的代码中，MatrixXf是一个行列可动态设置的矩阵，Vector3f是一个有3个元素的列向量。

typedef Matrix MatrixXf;
typedef Matrix Vector3f;

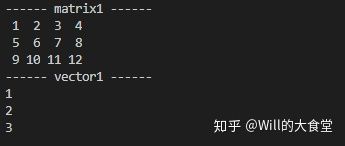
需要注意到是在定义矩阵大小时是没有初始化矩阵的，需要重新对矩阵进行初始化，这里是用Zero和Ones函数对其初始化，Zero是初始化为全0，而Ones是初始化为全1。最后，我们看一下执行结果。

当然，我们也可以给定任意值，每个值用逗号隔开，不过，这种方法只能适用于确定矩阵大小的情况下使用。

    Eigen::MatrixXf matrix1(3,4);
    Eigen::Vector3f vector1;

    matrix1 << 1, 2,  3,  4, 
               5, 6,  7,  8,
               9, 10, 11, 12;
    vector1 << 1, 2, 3;

执行结果如下：

另外，我们还可以用（）对某个元素进行访问，我们可以对其可读和可写。

    Eigen::MatrixXf matrix1(3,4);
    Eigen::Vector3f vector1;

    matrix1 << 1, 2,  3,  4, 
               5, 6,  7,  8,
               9, 10, 11, 12;
    vector1 << 1, 2, 3;

    matrix1(1,3) = 100;
    vector1(1) = 100;

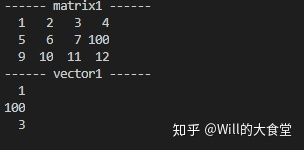
我们将matrix1的第2行，第4列修改成100；vector1的第2行修改成100，程序执行结果如下：

矩阵的基本运算

学习了矩阵的定义，那我们下面来看一下几个基本的矩阵运算。Matrix重载了+，+=，-，-+，×，×=，/，/=这几个基本的四则运算。

对于加减运算，需要注意一下几点：

• 左右矩阵的行列对应相等；
• 数据的类型也要相同，因为矩阵运算不支持隐式类型转换；
• 不支持和标量进行加减运算。

我们来看一个例子：

#include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{
    Eigen::MatrixXf matrix1(2,3);
    Eigen::MatrixXf matrix2(2,3);

    matrix1 << 1, 2, 3,
               5, 6, 7;

    matrix2 << 1, 1, 2,
               2, 1, 1;

    std::cout << "------ matrix1 ------" << std::endl << matrix1 << std::endl;
    std::cout << "------ matrix2 ------" << std::endl << matrix1 << std::endl;
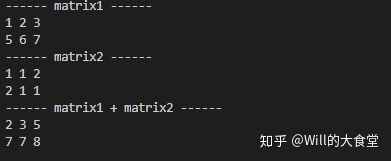
    std::cout << "------ matrix1 + matrix2 ------" << std::endl << matrix1 + matrix2 << std::endl;

}

执行结果如下：

关于乘除法运算，矩阵支持矩阵和标量之间的乘除法运算，标量和矩阵中的每个元素相运算。

#include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{
    Eigen::MatrixXf matrix1(2,3);
    Eigen::MatrixXf matrix2(2,3);

    matrix1 << 1, 2, 3,
               5, 6, 7;

    matrix2 << 1, 1, 2,
               2, 1, 1;

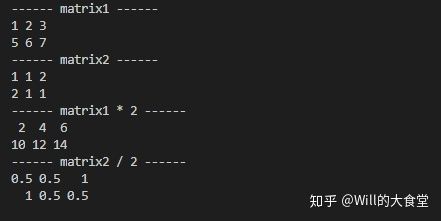
    std::cout << "------ matrix1 ------" << std::endl << matrix1 << std::endl;
    std::cout << "------ matrix2 ------" << std::endl << matrix2 << std::endl;
    std::cout << "------ matrix1 * 2 ------" << std::endl << matrix1 * 2 << std::endl;
    std::cout << "------ matrix2 / 2 ------" << std::endl << matrix2 / 2 << std::endl;

}

执行结果如下：

关于矩阵和矩阵之间的乘法，两个矩阵只有当左边的矩阵的列数等于右边矩阵的行数时,两个矩阵才可以进行矩阵的乘法运算 。如下图，左边矩阵第i行的元素逐个和右边矩阵第j列的元素相乘，乘积再相加，就是第i行，第j列的结果。对于Eigen库来说，它通过重载＊运算符帮我们实现了这个运算过程，我们直接使用＊运算符即可。

#include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{
    Eigen::MatrixXf matrix1(2,3);
    Eigen::MatrixXf matrix2(3,2);

    matrix1 << 1, 2, 3,
               5, 6, 7;

    matrix2 << 1, 1,
               2, 1,
               3, 1;

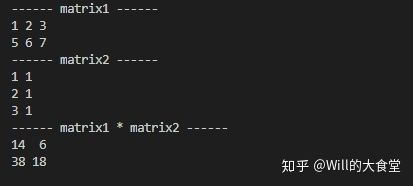
    std::cout << "------ matrix1 ------" << std::endl << matrix1 << std::endl;
    std::cout << "------ matrix2 ------" << std::endl << matrix2 << std::endl;
    std::cout << "------ matrix1 * matrix2 ------" << std::endl << matrix1 * matrix2 << std::endl;
}

执行结果如下：

另外，还包括矩阵的转置、共轭和共轭转置等矩阵运算，在Eigen中分别是有transpose（）、conjugate（）、adjoint（）函数可实现。

 #include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{
    Eigen::MatrixXf matrix1(2, 3);
    Eigen::MatrixXf matrix2(2, 3);

    matrix1 << 1, 2, 3,
               4, 5, 6;

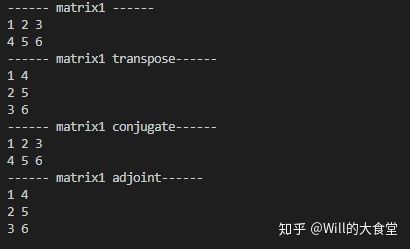
    std::cout << "------ matrix1 ------" << std::endl << matrix1 << std::endl;
    // 转置
    std::cout << "------ matrix1 transpose------" << std::endl << matrix1.transpose() << std::endl;
    // 共轭
    std::cout << "------ matrix1 conjugate------" << std::endl << matrix1.conjugate() << std::endl;
    // 共轭转置
    std::cout << "------ matrix1 adjoint------" << std::endl << matrix1.adjoint() << std::endl;

}

执行结果如下，不过，代码中实数的共轭还是其本身。

数组的定义和初始化

有的时候我们并不需要做线性代数矩阵运算，而只是做元素级的操作，这个时候就需要用到Array了。对Array来说，它和Matrix的定义和初始化的方式是一样的。

 #include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{

    Eigen::ArrayXXf array1(2,3);
    Eigen::ArrayXXf array2(3,3);
    Eigen::ArrayXXf array3(5,10);

    array1(0,0) = 1;
    array1(0,1) = 2;
    array1(0,2) = 2;
    array1(1,0) = 1;
    array1(1,1) = 2;
    array1(1,2) = 2;

    array2 << 1, 2, 3,
              4, 5, 6,
              7, 8, 9;

    array3 = Eigen::ArrayXXf::Ones(5, 10);


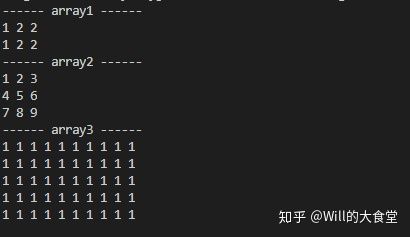
    std::cout << "------ array1 ------" << std::endl << array1 << std::endl;
    std::cout << "------ array2 ------" << std::endl << array2 << std::endl;
    std::cout << "------ array3 ------" << std::endl << array3 << std::endl;

}

这里的ArrayXXf也是Eigen库重定义的，它行和列数可以动态设置。我们可以看到Array的初始化和Matrix也是类似的 。

typedef Array  ArrayXXf;

下面是执行结果：

数组的基本运算

Array同样也重载了四则运算，但是，这里数据只是对数组内的元素做算术运算，而不是矩阵线性运算。所以，对于Array来数，两个数据的大小相同，即行数和行数相同，列数和列数相同，它的四则运算就是取两个数组相应位置的元素参与运算，运算的结果就是对应位置的值。

当然，也支持和标量之间的运算，数组中的每个元素都乘以这个标量，这个和矩阵一样。

#include 
#include "eigen_3_3_7/Eigen/Eigen"

int main()
{

    Eigen::ArrayXXf array1(2, 3);
    Eigen::ArrayXXf array2(2, 3);

    array1 << 1, 2, 3,
               4, 5, 6;

    array2 << 1, 2, 1,
              1, 1, 2;

    std::cout << "------ array1 ------" << std::endl << array1 << std::endl;
    std::cout << "------ array2 ------" << std::endl << array2 << std::endl;
    std::cout << "------ array1 + array2 ------" << std::endl << array1 + array2 << std::endl;
    std::cout << "------ array1 - array2 ------" << std::endl << array1 - array2 << std::endl;
    std::cout << "------ array1 * array2 ------" << std::endl << array1 * array2 << std::endl;
    std::cout << "------ array1 / array2 ------" << std::endl << array1 / array2 << std::endl;
    std::cout << "------ array1 * 2 ------" << std::endl << array1 * 2 << std::endl;


}

执行结果：

Matrix和Array两者是可以相互转换的。Matrix类有array()方法，可将Matrix转换为Array。Array类有matrix()方法，可将Array转换成Matrix。

总之，Eigen是一个很不错的开源库，官网还有更加详细的文档，大家可以参考：

http://eigen.tuxfamily.org/dox/GettingStarted.html

http://eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html

http://eigen.tuxfamily.org/dox/group__QuickRefPage.html

http://eigen.tuxfamily.org/dox/Eigen2ToEigen3.html

本文源于『Will的大食堂』，更多知识，请关注。

- End -