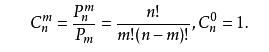求组合数——数学知识（c++）

组合数的公式：

一、递推（杨辉三角）

AcWing 885. 求组合数 I
给定n组询问，每组询问给定两个整数a，b，请你输出Cba mod (10⁹+7)的值。

输入格式
第一行包含整数n。

接下来n行，每行包含一组a和b。

输出格式
共n行，每行输出一个询问的解。

数据范围
1≤n≤10000,
1≤b≤a≤2000
输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

#include 
#include 

using namespace std;

const int N = 2010, mod = 1e9 + 7;


int c[N][N];//将所有的组合方式都预处理出来


void init()
{
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j <= i; j ++ )
            if (!j) c[i][j] = 1;//如果最后j为0，Ca/0为最终情况
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}


int main()
{
    int n;

    init();

    scanf("%d", &n);

    while (n -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);

        printf("%d\n", c[a][b]);
    }

    return 0;
}

二、乘法逆元

AcWing 886. 求组合数 II
给定n组询问，每组询问给定两个整数a，b，请你输出Cba mod (10⁹+7)的值。

输入格式
第一行包含整数n。

接下来n行，每行包含一组a和b。

输出格式
共n行，每行输出一个询问的解。

数据范围
1≤n≤10000,
1≤b≤a≤10⁵
输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, mod = 1e9 + 7;


int fact[N], infact[N];//fact表示阶乘,infact表示阶乘的逆元


int qmi(int a, int k, int p)//求逆元
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int main()
{
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i ++ )
    {
        fact[i] = (LL)fact[i - 1] * i % mod;//阶乘运算过程
        infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }


    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);//mod两次是为了防止结果过大,导致溢出
    }

    return 0;
}

三、卢卡斯定理

AcWing 887. 求组合数 III
给定n组询问，每组询问给定三个整数a,b,p，其中p是质数，请你输出Cba mod p的值。

输入格式
第一行包含整数n。

接下来n行，每行包含一组a,b,p。

输出格式
共n行，每行输出一个询问的解。

数据范围
1≤n≤20,
1≤b≤a≤10¹⁸,
1≤p≤10⁵,

输入样例：

3
5 3 7
3 1 5
6 4 13

输出样例：

3
3
2

#include 
#include 

using namespace std;

typedef long long LL;


int qmi(int a, int k, int p)//快速幂求a^k (mod p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b, int p)//计算c(a, b)
{
    if (b > a) return 0;

    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2, p) % p;
    }
    return res;
}


int lucas(LL a, LL b, int p)//公式：c(a, b) = c(a % p, b % p)·(a / p, b / p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}


int main()
{
    int n;
    cin >> n;

    while (n -- )
    {
        LL a, b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }

    return 0;
}

四、 质因数分解

乘法逆元只能处理模数为大质数的情况，卢卡斯定理只能处理模数为质数的情况，那有没有一种方法能处理模数不是质数的情况呢？显然是有的。而且不取模也是可以的。
我们可以把组合数中要乘或除的每一个数分解质因数，再把分母的质因数减掉，最后把剩下的质因数乘起来，边乘边模p就行了。
那如何分解质因数呢？可以用欧拉筛把每个数的最小质因数求出来，把i的最小质因数的编号保存在min_prime[i]里。
具体看代码吧。
AcWing 888. 求组合数 IV
输入a,b，求Cba的值。

注意结果可能很大，需要使用高精度计算。

输入格式
共一行，包含两个整数a和b。

输出格式
共一行，输出Cba的值。

数据范围
1≤b≤a≤5000
输入样例：

5 3

输出样例：

10

#include 
#include 
#include 

using namespace std;


const int N = 5010;

int primes[N], cnt;
int sum[N];
bool st[N];


void get_primes(int n)//线性筛素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)//得到n！中p的次数；
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)
//高精度乘法；
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}


int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);//得到C[a][b]中p的次数，因为是幂的形式，所以是减；
    }

    vector<int> res;
    res.push_back(1);//要先放进去一个1；

    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);

    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53401/
来源：AcWing

总结

写了这么多种算法，每种算法都有其优点与局限性。递推写起来快，思维简单，但时间复杂度高。乘法逆元用得比较普遍，因为一般都是模一个大质数，复杂度也几乎是线性的。卢卡斯定理只会在特定的题目里做到，但其实编程复杂度并不高，就是在乘法逆元的基础上加几句话。质因数分解的适用性最广，编程复杂度也最高，这就是完美的代价吧。