希尔排序的概念+实例
文章目录
- 一、基本概念
- 二、算法图解
- 三、代码实现
- 四、实例
一、基本概念
希尔排序:先追求表中部分有序,再逐渐逼近全局有序
具体步骤
先将待排序表分割成若干形如 L [ i , i + d , i + 2 d , . . . , i + k d ] L[i,i+d,i+2d,...,i+kd] L[i,i+d,i+2d,...,i+kd]的“特殊”子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止。
二、算法图解
我们举一个例子方便理解:对如下Arr[]数组元素进行由小到大排序(运用希尔排序)

第一轮次: d 1 = n / 2 = 4 第一轮次:d_1=n/2=4 第一轮次:d1=n/2=4
根据定义: L [ i , i + d , i + 2 d , . . . , i + k d ] L[i,i+d,i+2d,...,i+kd] L[i,i+d,i+2d,...,i+kd]的“特殊”子表
可以列出共有4个特殊子表
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 49 | 38 | 65 | 97 | 76 | 13 | 27 | 49 | |
| 子表1 | 49 | 76 | ||||||
| 子表2 | 38 | 13 | ||||||
| 子表3 | 65 | 27 | ||||||
| 子表4 | 97 | 49 |
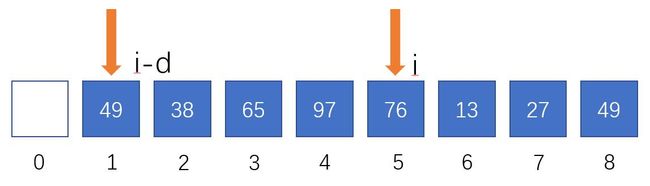
76 > 49 ; 无需插入排序; i + + ; 76>49;\\无需插入排序;\\i++; 76>49;无需插入排序;i++;

13 < 38 ; 需插入排序; 将 13 暂存在 A r r [ 0 ] 13<38;\\需插入排序;\\将13暂存在Arr[0] 13<38;需插入排序;将13暂存在Arr[0]
对13进行插入排序,从后往前寻找Arr[x]<13且Arr[x+1]>13的临界点(即插入位置)
并将寻找过的元素向后顺延一位
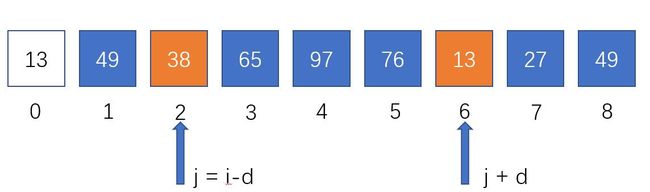
j 指向 i − d j指向i-d j指向i−d
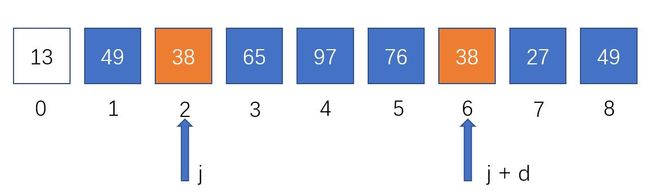
A r r [ j + d ] = A r r [ j ] Arr[j+d]=Arr[j] Arr[j+d]=Arr[j]

j < 0 ;退出循环; j<0;退出循环; j<0;退出循环;

令 A r r [ j + d ] = A r r [ 0 ] 令Arr[j+d]=Arr[0] 令Arr[j+d]=Arr[0]
第一轮排序完成后,得到如下
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 49 | 13 | 27 | 49 | 76 | 38 | 65 | 97 |
第二轮次: d 2 = d 1 / 2 = 2 第二轮次:d_2=d_1/2=2 第二轮次:d2=d1/2=2
根据定义: L [ i , i + d , i + 2 d , . . . , i + k d ] L[i,i+d,i+2d,...,i+kd] L[i,i+d,i+2d,...,i+kd]的“特殊”子表
可以列出共有2个特殊子表
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 49 | 13 | 27 | 49 | 76 | 38 | 65 | 97 | |
| 子表1 | 49 | 27 | 76 | 65 | ||||
| 子表2 | 13 | 49 | 38 | 97 |
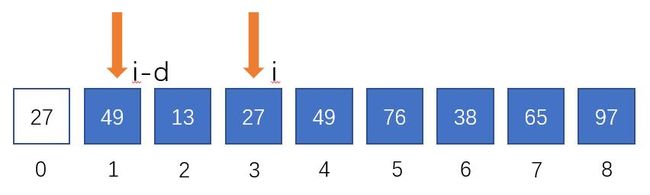
27 < 49 ; 需插入排序; 将 27 暂存在 A r r [ 0 ] ; 27<49;\\需插入排序;\\将27暂存在Arr[0]; 27<49;需插入排序;将27暂存在Arr[0];
仅关于两个元素的交换,与第一轮类似,略。

无需插入排序; i + + ; 无需插入排序;i++; 无需插入排序;i++;

无需插入排序; i + + ; 无需插入排序;i++; 无需插入排序;i++;
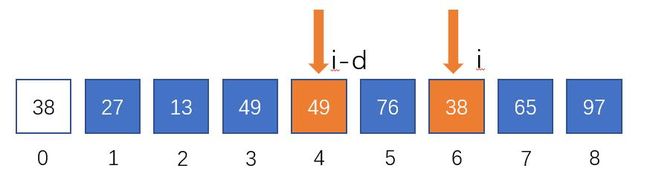
A r r [ i ] < A r r [ i − d ] ; 需插入排序;将 38 暂存在 A r r [ 0 ] ; Arr[i]

j指向i-d;从后往前寻找Arr[x]<38且Arr[x+1]>38的临界点(即插入位置);
并将寻找过的元素向后顺延一位

49 向后顺延; j − = d ; A r r [ j ] < A r r [ 0 ] ; 13 < 38 且 49 > 38 ;退出循环 49向后顺延;\\j-=d;\\ Arr[j]

A r r [ j + d ] = A r r [ 0 ] Arr[j+d]=Arr[0] Arr[j+d]=Arr[0]

i + + j = i − d ; 65 < 76 ;将 65 暂存到 A r r [ 0 ] i++\\j=i-d;\\ 65<76;将65暂存到Arr[0]\\ i++j=i−d;65<76;将65暂存到Arr[0]

A r r [ j + d ] = A r r [ j ] Arr[j+d]=Arr[j] Arr[j+d]=Arr[j]

j − = 2 ; 49 < 65 且 76 > 65 ; 退出循环 j-=2;\\ 49<65且76>65;退出循环\\ j−=2;49<65且76>65;退出循环
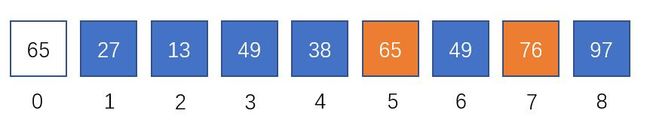
A r r [ j + d ] = A r r [ 0 ] Arr[j+d]=Arr[0] Arr[j+d]=Arr[0]
i++,重复如上操作,直至i=8
第二轮排序完成后,得到如下
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 27 | 13 | 29 | 38 | 65 | 49 | 76 | 97 |
d/=2,重复多个轮次,直至d=1
三、代码实现
void ShellSort(int Arr[], int length) {
for (int d = length / 2; d >= 1; d /= 2) {
for (int i = d + 1; i <= length; i++) {
if (Arr[i] < Arr[i - d]) {
Arr[0] = Arr[i];//Arr[0]暂存数据
int j;
//从后向前找临界点
for (j = i - d; j > 0 && Arr[j] > Arr[0]; j -= d) {//Arr[j]>Arr[0]而不是Arr[i]。Arr[i]在变化
Arr[j + d] = Arr[j];//向后顺延
}
//当Arr[j]Arr[0]。在Arr[j]的下一个位置插入Arr[0]
Arr[j + d] = Arr[0];
}
}
}
}
四、实例
7-12 排序
分数 25
作者 陈越
单位 浙江大学
给定N个(长整型范围内的)整数,要求输出从小到大排序后的结果。
本题旨在测试各种不同的排序算法在各种数据情况下的表现。各组测试数据特点如下:
数据1:只有1个元素;
数据2:11个不相同的整数,测试基本正确性;
数据3:103个随机整数;
数据4:104个随机整数;
数据5:105个随机整数;
数据6:105个顺序整数;
数据7:105个逆序整数;
数据8:105个基本有序的整数;
数据9:105个随机正整数,每个数字不超过1000。
输入格式:
输入第一行给出正整数N(≤10
5
),随后一行给出N个(长整型范围内的)整数,其间以空格分隔。
输出格式:
在一行中输出从小到大排序后的结果,数字间以1个空格分隔,行末不得有多余空格。
输入样例:
11
4 981 10 -17 0 -20 29 50 8 43 -5
输出样例:
-20 -17 -5 0 4 8 10 29 43 50 981
原题链接点这里
参考代码
#includeArr[0]。在Arr[j]的下一个位置插入Arr[0]
Arr[j + d] = Arr[0];
}
}
}
}
int main() {
int N;
scanf("%d", &N);
int Arr[N + 1];
//输入数据
for (int i = 1; i <= N; i++)
scanf("%d", &Arr[i]);
//希尔排序
ShellSort(Arr, N);
//打印排序后的数组
for (int i = 1; i <= N; i++) {
if (i != 1) {
printf(" ");
}
printf("%d", Arr[i]);
}
return 0;
}
