算法框架专辑60分版本

框架

动态规划

框架

经典例题

01背包&完全背包

dd大牛的《背包九讲》
AcWing在线题库-背包问题
一维解01背包为何要逆序

01背包问题描述：有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大

完全背包问题描述：有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大

记住这个结论

// ===01背包问题===
// 二维
for i=1..N
	for v=0..V
		f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}

// 一维
for i=1..N
	for v=V..0
		f[v]=max{f[v],f[v-c[i]]+w[i]};
		
【按照v=V..0的逆序来循环。这是因为要保证第i次循环中的状态f[i][v]是由状态f[i-1][v-c[i]]递推而来。换句话说，这正是为了保证每件物品只选一次，保证在考虑“选入第i件物品”这件策略时，依据的是一个绝无已经选入第i件物品的子结果f[i-1][v-c[i]]】

【为什么可以坍缩成一维数组：因为下一层只需要用到上一层的决策结果，比如第4层i=4只需要用到第三层的决策结果，不需要用到第二层和第一层的决策结果】

	

// ===完全背包===
// 三维
for i=1..N
	for j=0..V
		for k=0..k*v[j]<=j
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<= v}

// 一维
for i=1..N
	for v=0..V
		f[v]=max{f[v],f[v-c[i]]+w[i]}
// 【现在完全背包的特点恰是每种物品可选无限件，所以在考虑“加选一件第i种物品”这种策略时，却正需要一个可能已选入第i种物品的子结果f[i][v-c[i]]，所以就可以并且必须采用v= 0..V的顺序循环。这就是这个简单的程序为何成立的道理】		

状态方程的定义：即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。

如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”；如果放第i件物品（当前背包的容量能够装的下该物品），那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f [i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]

则其状态转移方程便是：f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}

01背包二维解法

1. v顺序

  public static void main(String[] args) {
    int v=10;   //背包体积c
    int n=5;    //物体个数n
    int[] c={0,2,2,6,5,4}; // 物品体积（ps：补充0是为了方便理解）
    int[] w={0,6,3,5,4,6}; // 物品价值
    int[][]dp=new int[n+1][v+1];
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <=v; j++) {
        if (j>=c[i]){
          dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);
        }else {
          dp[i][j]=dp[i-1][j];
        }
      }
    }
    System.out.println(dp[n][v]);
  }

运行过程

n \ v	0	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	6	6	6	6	6	6	6	6	6
2	0	0	6	6	9	9	9	9	9	9	9
3	0	0	6	6	9	9	9	9	11	11	14
4	0	0	6	6	9	9	9	10	11	13	14
5	0	0	6	6	9	9	12	12	15	15	15

2. v逆序遍历

  public static void main(String[] args) {
    int v=10;   //背包体积c
    int n=5;    //物体个数n
    int[] c={0,2,2,6,5,4}; // 物品体积（ps：补充0是为了方便理解）
    int[] w={0,6,3,5,4,6}; // 物品价值
    int[][]dp=new int[n+1][v+1];
    for (int i = 1; i <= n; i++) {
    // v逆序去遍历
      for (int j = v; j >=1; j--) {
        if (j>=c[i]){
          dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);
        }else {
          dp[i][j]=dp[i-1][j];
        }
        System.out.println("dp["+i+"]["+j+"]="+dp[i][j]);
      }
    }
    System.out.println(dp[n][v]);
  }

运行过程

n \ v	10	9	8	7	6	5	4	3	2	1	0
0	0	0	0	0	0	0	0	0	0	0	0
1	6	6	6	6	6	6	6	6	6	0	0
2	9	9	9	9	9	9	9	6	6	0	0
3	14	11	11	9	9	9	9	6	6	0	0
4	14	13	11	10	9	9	9	6	6	0	0
5	15	15	15	12	12	9	9	6	6	0	0

f[1][10]=max(f[0][10]=0,f[0][10-2=8]=f[0][8]=0+w[i]=0+6=6)=6
f[3][8]=max(f[2][8]=9,f[2][8-6=2]=f[2][2]=6+w[i]=6+5=11)=11
f[5][10]=max(f[4][10]=14,f[4][10-4=6]=f[4][6]=9+w[i]=9+6=15)=15

01背包一维解法

01背包一维为什么逆序

代码

  public static void main(String[] args) {
    int v = 10;   //背包体积c
    int n = 5;    //物体个数n
    int[] c = {0, 2, 2, 6, 5, 4}; // 物品体积（ps：补充0是为了方便理解）
    int[] w = {0, 6, 3, 5, 4, 6}; // 物品价值
    int[] dp = new int[v + 1];
    for (int i = 1; i <= n; i++) {
    // 注意这里不能写成j>=1
      for (int j = v; j >= c[i]; j--) {
        dp[j] = Math.max(dp[j], dp[j - c[i]] + w[i]);
        //System.out.println("dp[" + j + "]=" + dp[j]);
      }
    }
    System.out.println(dp[v]);
  }

运行过程

v	10	9	8	7	6	5	4	3	2	1	0
i=0	0	0	0	0	0	0	0	0	0	0	0
i=1	6	6	6	6	6	6	6	6
i=2	9	9	9	9	9	9	9	6	6
i=3	14	11	11	9	9
i=4	14	13	11	10	9	9
i=5	15	15	15	12	12	9	9

f[3 ][8]=max(f[2 ][8]=9,f[2 ][2]+5=6)=11
等价于：f[8]=max(f[8],f[2]+5)

ps:[3 ]加了删除线：只是为了方便理解

完全背包

  public static void main(String[] args) {
    int v = 10;   //背包体积c
    int n = 5;    //物体个数n
    int[] c = {0, 2, 2, 6, 5, 4}; // 物品体积（ps：补充0是为了方便理解）
    int[] w = {0, 6, 3, 5, 4, 6}; // 物品价值
    int[] dp = new int[v + 1];
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= v; j++) {
        if (j >= c[i]) {
          dp[j] = Math.max(dp[j], dp[j - c[i]] + w[i]);
          //System.out.println("dp[" + j + "]=" + dp[j]);
        } else {
          //System.out.println("dp[" + j + "]=" + dp[j]);
          dp[j] = dp[j - 1];
        }
      }
    }
    System.out.println(dp[v]);
  }

打印

v	0	1	2	3	4	5	6	7	8	9	10
i=0	0	0	0	0	0	0	0	0	0	0	0
i=1	0	0	6	6	12	12	18	18	24	24	30
i=2	0	0	6	6	12	12	18	18	24	24	30
i=3	0	0	6	6	12	12	18	18	24	24	30
i=4	0	0	0	0	0	4	18	18	24	24	30
i=5	0	0	0	0	6	6	18	18	24	24	30

f[1][4]=12和f[1][10]=30为例：当前只有一个物品，物品价格为6，为什么背包价值可以达到12,18,24,30，说明物品1被选了多次

f[1 ][2]=max(f[0 ][2]=0,f[0 ][2-2=0]+w[1]=f[1 ][0]=6)=6
此时f[1 ][2]的状态就已经不再是上一轮f[0 ][2]的状态了，而是被刷新成了本轮的f[1 ][2]状态，即1号物品被选了一次，
f[1 ][4]=max(f[0 ][4]=0,f[0 ][4-2=2]+w[1]=f[0 ][2]+6=12)=12，在新状态f[1 ][2]上1号物品又被选了一次即选了2次

拓展例题

Leetcode动态规划专题（共38道）

爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢

递归方式去写


// 初始状态（2种初状态）【找到有哪几种初状态】
f(1)=1,n=1
f(2)=2,n=2
// 递推方程（状态叠加的过程）
f(n)=f(n-1)+f(n-2),n>2

凑硬币/零钱兑换(完全背包)

给定硬币面额 coins=[1，2，5] 以及金额 N。问最少多少枚硬币可以凑出金额 N。其中硬币可以重复使用。

$$\begin{gathered} f(n)=min(f(n-1),f(n-2),f(n-5))+1 \\ ------------------ \\ f(n)=\underset{C_j=1,2,5}{\min }(f(n-c_j))+1,n>c_j \\ ------------------ \\ min(dp[i],dp[i-coin[j]]) \end{gathered}$$

丑数

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数

前10个丑数是：1, 2, 3, 4, 5, 6, 8, 9, 10, 12

$$\begin{gathered} 定义数组\text{dp}，其中\text{dp}[i]表示第i个丑数，第n个丑数即为\text{dp}[n]。由于最小的丑数是1，因此\text{dp}[1]=1。 \\ 如何得到其余的丑数呢？定义三个指针p_2,p_3,p_5，表示下一个丑数是当前指针指向的丑数乘以对应的质因数。 \\ 初始时，三个指针的值都是1。当2\le i\le n2时，令\text{dp}[i]=\min (\text{dp}[p_2]\times 2,\text{dp}[p_3]\times 3,\text{dp}[p_5]\times 5)， \\ 然后分别比较\text{dp}[i]和\text{dp}[p_2]\times 2,\text{dp}[p_3]\times 3,\text{dp}[p_5]\times 5是否相等，如果相等则将对应的指针加1。 \end{gathered}$$

class Solution {
    public int nthUglyNumber(int n) {
        int[] dp = new int[n + 1];
        dp[1] = 1;
        int p2 = 1, p3 = 1, p5 = 1;
        for (int i = 2; i <= n; i++) {
            int num2 = dp[p2] * 2, num3 = dp[p3] * 3, num5 = dp[p5] * 5;
            dp[i] = Math.min(Math.min(num2, num3), num5);
            if (dp[i] == num2) {
                p2++;
            }
            if (dp[i] == num3) {
                p3++;
            }
            if (dp[i] == num5) {
                p5++;
            }
        }
        return dp[n];
    }
}

最长递增子序列

状态定义：dp[i] 的值代表 nums 以 nums[i] 结尾的最长子序列长度
转移方程：dp[i] = max(dp[i], dp[j] + 1) for j in [0, i)

• 状态数组维护局部最大
• max变量维护全局最大
• dp[i] = Math.max(dp[i], dp[j] + 1)

public int lengthOfLIS(int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    int[] dp = new int[nums.length];
    dp[0] = 1;
    int max = 1;
    for (int i = 1; i < nums.length; i++) {
        dp[i] = 1;
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) {
                //状态数组维护局部最大
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
        //max变量维护全局最大
        max = Math.max(max, dp[i]);
    }
    return max;
}

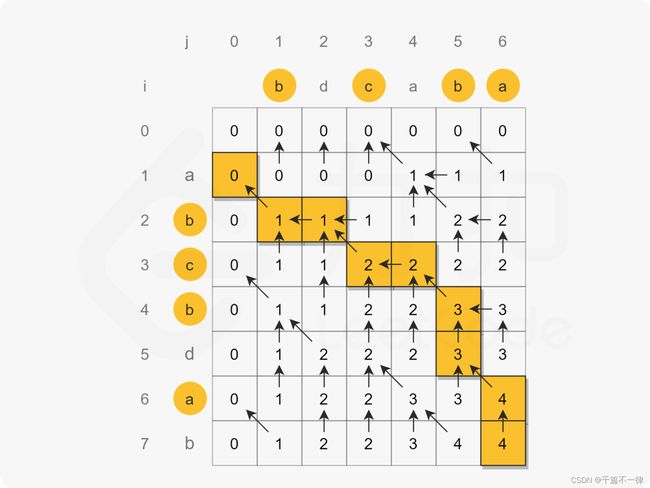
最长公共子序列

最长公共子序列问题是典型的二维动态规划问题

写出状态方程，然后猜测递推方程，可以找几种情况来分析一下，不用陷入到每一步的推演上

状态定义：定义 dp[i][j] 表示 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列。 （注：text1[0:i-1] 表示的是 text1 的 第 0 个元素到第 i - 1 个元素，两端都包含），之所以 dp[i][j] 的定义不是 text1[0:i] 和 text2[0:j] ，是为了方便当 i = 0 或者 j = 0 的时候，dp[i][j]表示的为空字符串和另外一个字符串的匹配，这样 dp[i][j] 可以初始化为 0.

状态转移：
$$dp[i][j]=\{\begin{array}{ll}dp[i-1][j-1]+1,& \text{text1[i - 1] == text2[j - 1]}\\ max(dp[i-1][j],dp[i][j-1])& \text{text1[i−1] != text2[j−1]}\end{array}$$

public int longestCommonSubsequence(String text1, String text2) {
    int m = text1.length(), n = text2.length();
    int[][] dp = new int[m + 1][n + 1];
    for (int i = 1; i <= m; i++) {
        char c1 = text1.charAt(i - 1);
        for (int j = 1; j <= n; j++) {
            char c2 = text2.charAt(j - 1);
            if (c1 == c2) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
}

子数组的最大和

状态定义：f(i)代表以第i个数结尾的「子数组的最大和」
转移方程：f(i)=max{f(i−1)+nums[i],nums[i]}
补充: sum(j)=max{sum(j−1)+arr[j],arr[j]}

public int maxSubArray(int[] nums) {
    int pre = 0, maxAns = nums[0];
    for (int x : nums) {
        pre = Math.max(pre + x, x);
        maxAns = Math.max(maxAns, pre);
    }
    return maxAns;
}

使用最小花费爬楼梯—滚动数组优化空间

$$\begin{gathered} 上述代码的时间复杂度和空间复杂度都是O(n)O(n)。 \\ 注意到当i\ge 2i\ge 2时，\text{dp}[i]dp[i]只和\text{dp}[i-1]dp[i-1]与\text{dp}[i-2]dp[i-2]有关 \\ 因此可以使用滚动数组的思想，将空间复杂度优化到O(1)O(1)。 \end{gathered}$$

  public int minCostClimbingStairs(int[] cost) {

    if (cost.length == 1) {
      return cost[0];
    }
    int[] dp = new int[cost.length];
    dp[0] = cost[0];
    dp[1] = cost[1];
    for (int i = 2; i < cost.length; i++) {
      dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
    }
    return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
  }

  public int minCostClimbingStairs(int[] cost) {

    if (cost.length == 1) {
      return cost[0];
    }
    int[] dp = new int[3];
    dp[0] = cost[0];
    dp[1] = cost[1];
    for (int i = 2; i < cost.length; i++) {
      dp[2] = Math.min(dp[1], dp[0]) + cost[i];
      dp[1]=dp[2];
      dp[0]=dp[1];
    }
    return Math.min(dp[1], dp[2]);
  }

滚动数组优化

前提概要
滚动数组是一种能够在动态规划中降低空间复杂度的方法，有时某些二维dp方程可以直接降阶到一维，在某些题目中甚至可以降低时间复杂度，是一种极为巧妙的思想。

简要来说就是通过观察dp方程来判断需要使用哪些数据，可以抛弃哪些数据，一旦找到关系，就可以用新的数据不断覆盖旧的数据量来减少空间的使用。

#include
using namespace std;
int main()
{
    int a[3];
    a[0] = 1;
    a[1] = 1;
    for(int i = 1;i <= 35;i++)
    {
        a[2] = a[0] + a[1];
        a[0] = a[1];
        a[1] = a[2];
    }
    printf("%d\n",a[2]); 
    return 0;
}

通过观察斐波那契数列方程 f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n) = f(n-1) + f(n-2)f(n)=f(n−1)+f(n−2)，
我们可以发现，实际上只需要前两个递推的数求和即可，于是我们可以使用数组的前三个位置来分别存贮数据，再用递推得到的新数据将旧数据覆盖。
这样我们本来需要用三十多个位置的数组，最终却只用了三个位置，大大减少了空间复杂度。对于某些只需要最终答案的题目，我们可以抛弃掉当中一些不必要存贮的数据，来减少空间的使用。
小结
对于动态规划题目来说，我们可以先写出最原始的dp方程，再通过观察dp方程，使用滚动数组进行优化，我们需要思考如何更新数据和覆盖数据来达到降维的目的（可能需要很长的时间思考，不过熟能生巧）
滚动数组

public int minCostClimbingStairs(int[] cost) {

    if (cost.length == 1) {
      return cost[0];
    }
    int[] dp = new int[3];
    dp[0] = cost[0]; // pre=cost[0]
    dp[1] = cost[1]; // cur=cost[1]
    for (int i = 2; i < cost.length; i++) {
        // next = Math.min(pre, cur) + cost[i];
        // pre = cur;
        // cur = next;
      dp[2] = Math.min(dp[1], dp[0]) + cost[i];
      dp[0]=dp[1];
      dp[1]=dp[2];
    }
    return Math.min(dp[1], dp[0]);
  }

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int prev = 0, curr = 0;
        for (int i = 2; i <= n; i++) {
            int next = Math.min(curr + cost[i - 1], prev + cost[i - 2]);
            prev = curr;
            curr = next;
        }
        return curr;
    }
}

最长公共连续子序列
最长重复子数组

不同路径------二维化一维

如何把二维化作一维=滚动数组

[是一个理解动态规划如何工作非常好的例子–不要陷入到执行过程，写出动态方程定义以及递推方程，在注意一下状态方程的初始状态]

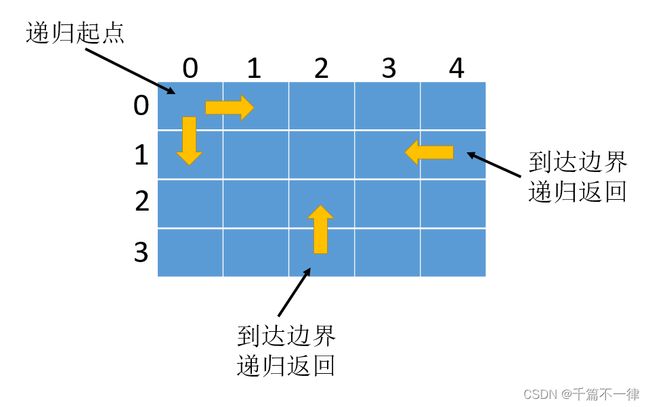
func uniquePaths(m int, n int) int {
	arr := make([][]int, m)
	for i := 0; i < m; i++ {
		arr[i] = make([]int, n)
		arr[i][0] = 1
	}
	for j := 0; j < n; j++ {
		arr[0][j] = 1
	}

	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			arr[i][j] = arr[i-1][j] + arr[i][j-1]
		}
	}
	return arr[m-1][n-1]
}

class Solution {
    public int uniquePaths(int m, int n) {
        //一维空间，其大小为 n
        int[] dp = new int[n];
        Arrays.fill(dp, 1);
        for(int i = 1; i < m; ++i) {
            for(int j = 1; j < n; ++j) {
                //等式右边的 dp[j]是上一次计算后的，加上左边的dp[j-1]即为当前结果
                dp[j] = dp[j] + dp[j - 1];
            }
        }
        return dp[n - 1];
    }   
}

整数拆分（感受数学之美）

整数拆分：非常严谨优雅的数学论证推理

分割等和子集（转化问题的问法，降低原问题的复杂度）

• 给定一个非空的正整数数组 nums ，请判断能否将这些数字分成元素和相等的两部分。
• 给定一个只包含正整数的非空数组 nums，判断是否可以从数组中选出一些数字，使得选出的这些数字的和刚好等于整个数组的元素和的一半

题目是在误导/迷惑你朝着错误的方向思考

非常漂亮的讲解
本题本质上是一道「0−1 背包问题」：给定一个只包含正整数的非空数组 nums，判断是否可以从数组中选出一些数字，使得选出的这些数字的和刚好等于整个数组的元素和的一半。

程序执行前可先判断 nums 是否可以等分，若不能则可直接返回 False

最后一块石头的重量 II

简单来说就是任意选i块石头，使得他们的重量趋近于总重量的一半，因为这样和另一半抵消的差值就是最小的
$$本问题可以看作是背包容量为\lfloor sum/2\rfloor ，物品重量和价值均为stonesi\text{的}0-1背包问题$$

参考解法
01背包：不超过背包容量使得价值最大（第i个物品背包容量为v的最大价值）

即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值
$$f[i][v]=max\{\begin{array}{ll}f[i-1][v],& \text{(}不选)\\ f[i-1][v-c[i]]+w[i],& \text{(}选)\end{array}$$

原来dp可以是个布尔数组
分割等和子集选一些数能够满足和为1/2数组和（第i个物品和是否为j的布尔值）

dp[i][j] = dp[i−1][j] || dp[i−1][j−nums[i]]

原来可以这样转换
最后一块石头的重量：选一些数使其最接近1/2数组和---- 第i个物品和不超过j的最大值

f[i][j] = max(f[i-1][j],f[i-1][j-num[i]]+num[i]) ???

目标和：添加一些正负号有多少方案使其等于目标和 ：选一些数使其和等于(sum-target)/2，问有几种选择法(第i个物品和为j的方案数)

f[i][j] = f[i-1][j]+f[i-1][j-num[i]]

原来dp可以是三维的
一和零：这是一个三维的01背包问题

1 2 1 2 1 2 = sum

负号元素和为f，整号元素和为sum-f
$$\begin{gathered} target=sum-f-f=sum-2f \\ (sum-target)/2=f \end{gathered}$$

定义 f[i][j]代表考虑前 i 个物品（数值），凑成总和不超过 j 的最大价值。

每个物品都有「选」和「不选」两种决策，转移方程为：
$$f[i][j]=max(f[i-1][j],f[i-1][j-stones[i-1]]+stones[i-1])$$

完全平方数

贪心不行v
可能是个完全背包模型—用了贪心去验证/实现起来好复杂（12【9，4，1】(1…3)…12-9，12-4好像递推不上了，该方案不行—其实是min（12-9，12-4））----最后否了该方案

可能是个完全背包模型—复杂？处理方式不对而已（30【25，16，9，4，1】(1…5)）—我觉得这步实现太复杂。就否定了该方案，实际实现特别简单

递归回溯

递归解题三部曲

回溯法讲解

框架

func rcs(循环变量i){
   递归出口：
     {
     进行操作
     }
 
   // 如果选择只有2个，就不用for了，直接如下操作，典型场景就是二叉树的遍历
   // rcs（i+1，选）  
   // rcs(i+1,不选)
   
   // 否则
   for（穷举每个选择进行递归）{
     //状态标记
     rcs(i+1)
     //清除状态
   }
}

经典例题

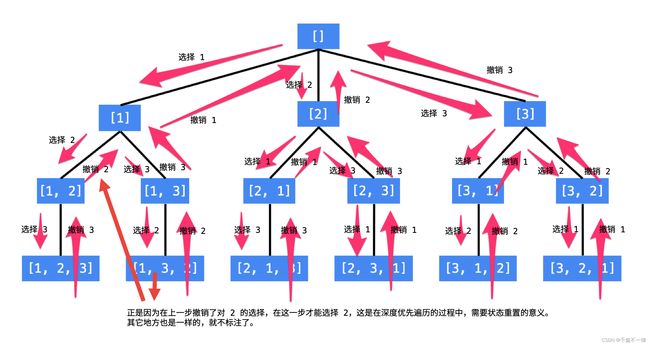
子集

func subsets(nums []int) [][]int {
	var res [][]int
	var temp []int //golang中递归函数的全局变量还是尽量放在递归函数中
	var rcs func(int)
	rcs = func(i int) {
		if i == len(nums) {
			res = append(res, append([]int(nil), temp...)) //所以res中的temp必须是新的引用，不能是全局temp的引用
			res = append(res, temp)                        //因为temp是全局的，temp[:len(temp)-1]该局部操作会改变已计算好的结果，比如原res[[1 2 3] [1 2]]经过添加了temp[1,3],其原来的1,2中的2会被移除，替换成3，就变成了[[1 3 3] [1 3] [1 3]]
			return
		}
		temp = append(temp, nums[i])
		rcs(i + 1)
		temp = temp[:len(temp)-1]
		rcs(i + 1)
	}
	rcs(0)
	return res
}

排列

func permute(nums []int) [][]int {
	var res [][]int
	var path []int
	used := make([]bool, len(nums))
	var rcs func(int)
	rcs = func(i int) {
		if i == len(nums) {
			res = append(res, append([]int(nil), path...))
			return
		}
		for j := 0; j < len(nums); j++ {
			if used[j] == true {
				continue
			}
			path = append(path, nums[j])
			used[j] = true
			rcs(i + 1)
			path = path[:len(path)-1]
			used[j] = false
		}
	}
	rcs(0)
	return res
}

组合

rcs(j + 1)可以对比排列中的rcs(i + 1)，并思考为什么这里不能这样写，我觉得非常有意义

func combine(n int, k int) [][]int {
	var nums []int
	for i := 1; i <= n; i++ {
		nums = append(nums, i)
	}
	var res [][]int
	var path []int
	used := make([]bool, len(nums))
	var rcs func(int)
	rcs = func(i int) {
		if len(path) == k {
			res = append(res, append([]int(nil), path...))
			return
		}
		for j := i; j < len(nums); j++ {
			if used[j] == true {
				continue
			}
			path = append(path, nums[j])
			used[j] = true
			rcs(j + 1) //这里必须写成j+1，因为j是带路径记忆的变量即在递归中j变化0123,123,233，如果写成i+1，那么j变化就是0123,123，21233123
			used[j] = false
			path = path[:len(path)-1]
		}
	}
	rcs(0)
	return res
}

二叉树&多叉树

框架

树中每个节点属于以下三种类型之一：

叶子：如果这个节点没有任何孩子节点。【Leaf】
根：如果这个节点是整棵树的根，即没有父节点。【Root】
内部节点：如果这个节点既不是叶子节点也不是根节点。【Inner】

二叉树的定义

public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    TreeNode(int value) { this.value = value; }
}

二叉树的遍历

void helper(TreeNode root){
    if (root == null) {
        return;
    }
    System.out.println(root.value);//前序遍历
    helper(root.left);
    //System.out.println(root.value);中序遍历
    helper(root.right);
    //System.out.println(root.value);后序遍历
}

二叉树的节点统计

public int countNodes(TreeNode root) {
    return root == null ? 0 : 1 + countNodes(root.left) + countNodes(root.right);
}

经典例题

二叉树的最大深度

int max=0;
int helper(TreeNode root,int max){
    if (root == null) {
        if (max>this.max) this.max=max;
        return this.max;
    }
    helper(root.left,max+1);
    helper(root.right,max+1);
    return this.max;
}

二叉树的最近公共祖先-（递归后置操作的经典）

TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || p == root || q == root) {
        return root;
    }
    TreeNode l = lowestCommonAncestor(root.left, p, q);
    TreeNode r = lowestCommonAncestor(root.right, p, q);
    return l == null ? r : (r == null ? l : root);
}

辅助理解

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//        如果根节点为空直接返回null
        if(root == null){
            return null;
        }
//        第一个找到的节点为q说明q比p深度小,位于p上方,直接返回q
        if(root.val == q.val){
            return q;
//        第一个找到的节点为p说明p比q深度小,位于q上方,直接返回p
        }else if(root.val == p.val){
            return p;
        }else {
//            left和right分别表示向左右递归得到的结果
            TreeNode left = lowestCommonAncestor(root.left,p,q);
            TreeNode right = lowestCommonAncestor(root.right,p,q);
//            如果left和right都不为空说明两个节点在根节点左右,直接返回根节点
            if(left != null && right != null){
                return root;
//            如果左边递归为空说明两个节点都在右边,且right节点一定是p,q的根节点,直接返回right节点
            }else if(left == null){
                return right;
            }else {
//            如果右递归为空说明两个节点都在左边,且left节点一定是p,q的根节点,直接返回left节点
                return left;
            }
        }
    }
}

二叉树：平衡/完全/搜索树的判断

二叉树高度计算
$$height[i]=\{\begin{array}{ll}0& \text{p 是空节点}\\ max(height(p.left),height(p.right))+1& \text{p 是非空节点}\end{array}$$

平衡二叉树的判断

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        } else {
            return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        }
    }
    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return Math.max(height(root.left), height(root.right)) + 1;
        }
    }
}

验证二叉搜索树

中序遍历时，判断当前节点是否大于中序遍历的前一个节点，如果大于，说明满足 BST，继续遍历；否则直接返回 false。

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        // 访问左子树
        if (!isValidBST(root.left)) {
            return false;
        }
        // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历。
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        // 访问右子树
        return isValidBST(root.right);
    }
}

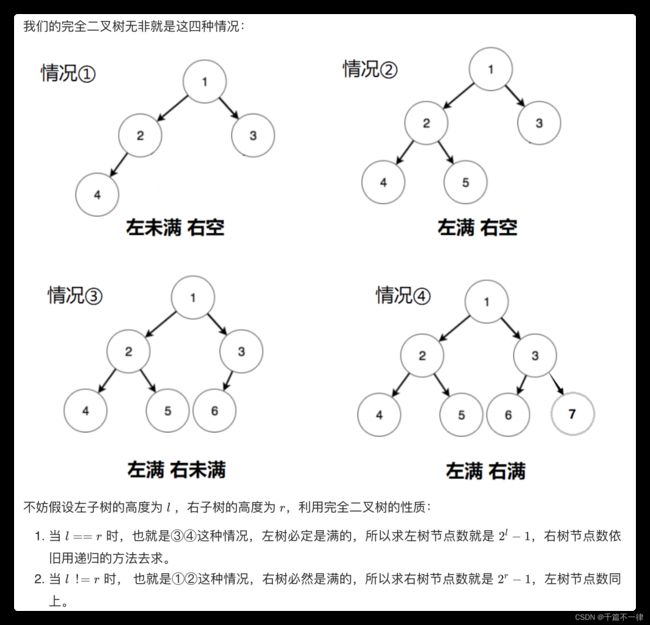
完全二叉树的节点数

定义：左节点小于根节点，右节点大于根节点（左小右大）

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        int l = getHeight(root.left); // 求左树高
        int r = getHeight(root.right); // 求右树高
        // 左必满 Math.pow(2, l) - 1 + 右树高 + 1
        if (l == r) return (1 << l) + countNodes(root.right);
        // 右必满 Math.pow(2, l) - 1 + 左树高 + 1
        else return (1 << r) + countNodes(root.left);
    }
    // 求树高
    public int getHeight(TreeNode root) {
        int height = 0;
        while (root != null) {
            // 因为完全二叉树是基于左节点的 所以我们可以遍历到最深的左节点 此时的height就是树高
            root = root.left; 
            height++;
        }
        return height;
    }
}

求数组的所有子集(选不选问题)

void getArr(List<Integer> list, List<List<Integer>> result, List<Integer> temp, int level){
    if(level == list.size()){ result.add(temp); }
    else{
        //不选
        getArr(list, result, new ArrayList<>(temp), level + 1);
        temp.add(list.get(level));
        //选
        getArr(list, result, new ArrayList<>(temp), level + 1);
    }
}

思路：使用二叉树来构建含有子集的叶子节点，每一层代表一个元素，左子树代表不使用该节点，右子树代表使用该节点，使用中序遍历来获得全部叶子结点，那么就能获得该数组的子集。

思路图（选不选问题的分析图是这么画的）

回溯法对01背包问题的描述

public class Main {
    int n=4;
    int c=2;
    int[] v={1,2,3,4};
    int[] w={1,1,1,2};
    static int bestV=0;
    
    public void bk(int depth,int preW,int preV) {
        int curW=preW;
        int curV=preV;
        if (depth>=n){ //达到最大深度否
            if (bestV<curV) bestV=curV;
            return;
        }
        if (curW+w[depth]<=c){ //满足约束条件否
            curW+=w[depth];
            curV+=v[depth];
            //选取了第i件物品
            bk(depth+1,curW,curV);
            curW-=w[depth];
            curV-=v[depth];
        }
        //不选取第i件物品
        bk(depth+1,curW,curV);
    }
    public static void main(String[] args) {
        new Main().bk(0, 0, 0);
        System.out.println(bestV);
    }
}

全排列

List<List<Integer>> res = new ArrayList<>();
int[] visited = new int[nums.length];//初始化数组，默认初值全为0
List<Integer>temp=new ArrayList<Integer>();

void backtrack(List<List<Integer>> res, int[] nums, ArrayList<Integer> tmp, int[] visited) {
    if (tmp.size() == nums.length) {
        res.add(new ArrayList<>(tmp));
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        //已经遍历过的直接跳到下一节点
        if (visited[i] == 1) continue;
        //遍历过的节点打上标记
        visited[i] = 1;
        tmp.add(nums[i]);
        backtrack(res, nums, tmp, visited);
        visited[i] = 0;
        tmp.remove(tmp.size() - 1);
    }
}

见pdf(为何递归前要交换元素:是让已经选过的元素在左边，未选过的元素在右边，为何递归结束要交换元素:恢复现场，保证子问题相互独立且与原问题性质相同)

void helper(int[] arr, int i) {
    if (i > arr.length) { return; }
    if (i == arr.length) { System.out.println(arr); }
    for (int j = i; j < i; j++) {
        swap(arr[i], arr[j]);
        helper(arr, i + 1);
        swap(arr[i], arr[j]);
    }
}
void swap(int i, int j) {}

组合

友情提示：对于这一类问题，画图帮助分析是非常重要的解题方法。

public class Solution {

    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        // 从 1 开始是题目的设定
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        // 递归终止条件是：path 的长度等于 k
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 遍历可能的搜索起点
        for (int i = begin; i <= n; i++) {
            // 向路径变量里添加一个数
            path.addLast(i);
            // 下一轮搜索，设置的搜索起点要加 1，因为组合数理不允许出现重复的元素
            dfs(n, k, i + 1, path, res);
            // 重点理解这里：深度优先遍历有回头的过程，因此递归之前做了什么，递归之后需要做相同操作的逆向操作
            path.removeLast();
        }
    }
}

滑动窗口

滑动窗⼝法，也叫尺取法（可能也不⼀定相等，⼤概就是这样 =。=），可以⽤来解决⼀些查找满⾜⼀ 定条件的连续区间的性质（⻓度等）的问题。由于区间连续，因此当区间发⽣变化时，可以通过旧有的 计算结果对搜索空间进⾏剪枝，这样便减少了重复计算，降低了时间复杂度。往往类似于“请找到满⾜ xx的最x的区间（⼦串、⼦数组）的xx”这类问题都可以使⽤该⽅法进⾏解决。 滑动窗⼝法可以⽤来解决⼀些查找满⾜⼀定条件的连续区间的性质（⻓度等）问题，个⼈认为可以看做 是⼀种双指针⽅法的特例，两个指针都起始于原点，并⼀前⼀后向终点前进。还有⼀种双指针⽅法，
两个指针⼀始⼀终，并相向靠近，这种⽅法的内在思想和滑动窗⼝也⾮常类似，如Leetcode11. 盛最多 ⽔的容器就可以使⽤这种解法求解。 双指针：【快慢指针（⼜叫滑动窗⼝）+双端指针】

框架

int left = 0, right = 0;

while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    right++;
	// 判断左侧窗口是否要收缩
    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
        // 进行窗口内数据的一系列更新
    }
} 

时间复杂度： O(N)

注意点：
①适用于子串问题；
②什么时候缩小窗口取决于题意；
比如：题目要求子串不得有重复字符。那么当窗口扩大到包含重复字符时，就需要收缩窗口了。
③什么时候计算窗口大小（往往窗口大小就是答案）；
在window满足题目条件时，就可以计算窗口大小了，即res = right - left；；当然了，题目往往要求最优解，所以要更新res，寻求最优解。
④最好增加个预判：if(sizeS < sizeT) return res

经典例题

最长不重复子字符串

abacadbeaa
滑动窗口左右2边都可以收缩，收缩的条件是保证当前窗口里面的元素是不重复的子字符串。当遇到重复就要丢弃之前的窗口（1：左指针划到当前元素来正确应该是2：左指针划到最大重复的下标+1），从当前元素重新开始窗口（如果按照1，就是adbe，按照2是cadbe）

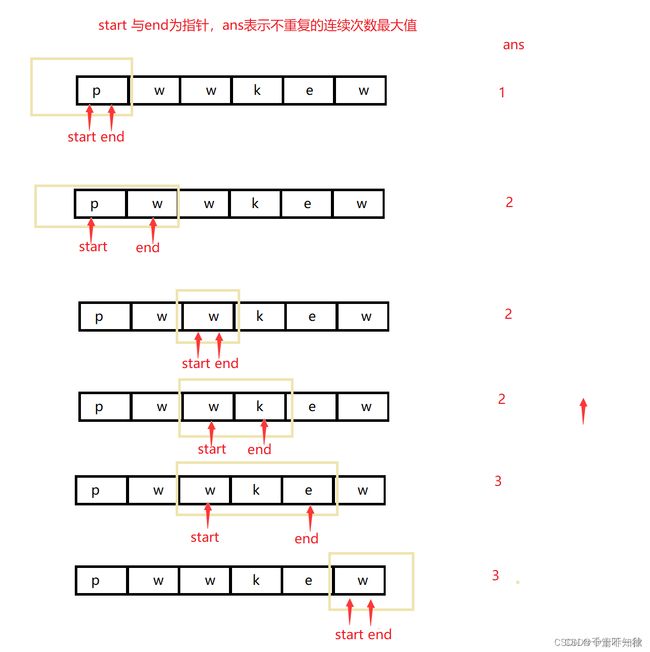
重点在这里：

left = Math.max(left,map.get(s.charAt(i)) + 1);

自己容易犯的错

left,right,map;
while(right<list.size()){
if(map.contain(list(right))){
	// 错误的
	//left=right
	//right++;
}
right++;
max = math(max,right-left)
}
return max;

正确的

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0) return 0 ;
        HashMap<Character,Integer> map = new HashMap<>();
        int max=0;
        int left = 0;
        for(int i =0;i<s.length();i++){
            if(map.containsKey(s.charAt(i))){
                left = Math.max(left,map.get(s.charAt(i)) + 1);
            }
            map.put(s.charAt(i), i);
            max = Math.max(max,i-left+1);
        }
        return max;
    }
}
//

重复的DNA序列

func findRepeatedDnaSequences(s string) []string {
	l := 0
	m := map[string]int{}
	var arr []string
	for i, _ := range s {
		if i >= 9 {
			sub := s[l : i+1]
			if mv, ok := m[sub]; ok {
				m[sub] = mv + 1
				if m[sub] == 1 {
					arr = append(arr, sub)
				}
			} else {
				m[sub] = 0
			}
			l++
		}
	}
	return arr
	// c++/golang的map[key]++语法相当于 Java 的map.put(key, map.get(key)+ 1)
}

链表

基本操作

type ListNode struct {
	Val  int
	Next *ListNode
}

func InitListNode(arr []int) *ListNode {
	dummy := &ListNode{
		Val: 0,
	}
	cur := dummy
	for _, v := range arr {
		aa := &ListNode{
			Val: v,
		}
		cur.Next = aa
		cur = cur.Next
	}
	return dummy.Next
}

框架

虚拟节点/哑节点：【1.记录原始表头的位置；2.防止空指针（ 链表总共有 5 个节点，题目就让你删 除倒数第 5 个节点，也就是第一个节点，那按照算法逻辑，应该首先找到倒数第 6 个节点。但第一个节点前 面已经没有节点了，这就会出错 ）】链表记录的是引用，传递的也是引用，链表结构改变了，但引用不会改变（遍历前需要额外记录表头，遍历后需要使用返回的结果更新表头）

经典例题

反转链表

假设链表为 1→2→3→∅1, 我们想要把它改成 ∅←1←2←3

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

这是我第10次接触这个题：就是我没有深深的理解这句话，忽视了这句话，导致10次做出来都是错的：所以我实践了10次，却没有提取出一次正确的认识，没有记住这个认识，没有反复重复实践这个认识

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/fan-zhuan-lian-biao-lcof/solutions/551600/fan-zhuan-lian-biao-by-leetcode-solution-jvs5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

链表的哲学：我想复杂啦，还引入了头节点,我想它会运行的很好的，可实际确是死循环：我自己也画图了，可却人为按照主观想法靠想象补充了许多客观/实际运行的缺乏的操作（链表全部用迭代来做，不要用递归）

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode cur = head;
        ListNode dummy = new ListNode(0);
        dummy.next=cur;
        while(cur.next!=null){
            cur.next.next=cur;
            dummy.next=cur.next;
            cur=cur.next;
        }
        return dummy.next;
    }
}

反转链表 II(部分反转)

public ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case------写的很妙
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}

ListNode after; //必须放在这里
ListNode reverseN(ListNode head, int n) {
    //还有一个错误，after的赋值是在递归出口处赋值的，该值会在一次函数递归结束后失效
    //该声明写在这里它的作用域就是整个函数
    //ListNode after = null;会带来如下错误
    //输入：[1,2,3,4,5] 2
    //输出[1,4,3,2]，预期[1,4,3,2,5]
    if (n == 1) {
        //该赋值操作如果不是在递归出口，那本次赋值对整个函数都有效
        //该赋值操作如果在递归出口，那本次赋值出了这个代码块就不生效了
        after = head.next;
        return head;
    }
    ListNode last = reverseN(head.next, n - 1);
    head.next.next = head;
    head.next = after;
    return last;
}

func reverseBetween(head *ListNode, left int, right int) *ListNode {
	if head.Next == nil {
		return head
	}
	dummy := &ListNode{
		Val: 0,
	}
	dummy.Next = head
	cur := dummy
	index := 0
	for index != left-1 {
		index++
		cur = cur.Next
	}
	sp := cur
	sn := cur.Next
	index++
	cur = cur.Next
	rPrev := cur
	index++
	cur = cur.Next
	for index != right+1 {
		rNext := cur.Next
		cur.Next = rPrev
		rPrev = cur
		cur = rNext
		index++
	}
	fp := rPrev
	fn := cur
	sp.Next = fp
	sn.Next = fn
	return dummy.Next
}

K 个一组翻转链表

func reverseKGroup(head *ListNode, k int) *ListNode {
	if k == 1 {
		return head
	}
	dummy := &ListNode{Val: -1}
	dummy.Next = head
	cur := head
	index := 1
	prev := dummy
	start := head
	for cur != nil {
		index++
		cur = cur.Next
		if cur == nil { //(cur == nil && index%k != 0)||(cur == nil && index%k == 0)
			prev.Next = start
		} else if index%k == 0 && cur != nil {
			nextCur := cur.Next
			cur.Next = nil
			rvsResult := reverseList(start)
			prev.Next = rvsResult
			cur = nextCur
			prev = start
			start = nextCur
			index++
		}
		//cur != nil && index%k != 0 不做处理
	}
	return dummy.Next
}

func reverseList(head *ListNode) *ListNode {
	var prev *ListNode
	var cur *ListNode
	prev = nil
	for cur = head; cur.Next != nil; {
		nt := cur.Next
		cur.Next = prev
		prev = cur
		cur = nt
	}
	cur.Next = prev
	return cur
}

合并两个有序链表

func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
	dummy := &ListNode{Val: -1}
	cur := dummy
	for list1 != nil || list2 != nil {
		if list1 == nil {
			cur.Next = &ListNode{Val: list2.Val}
			cur = cur.Next
			list2 = list2.Next
			continue
		}
		if list2 == nil {
			cur.Next = &ListNode{Val: list1.Val}
			cur = cur.Next
			list1 = list1.Next
			continue
		}
		val1 := list1.Val
		val2 := list2.Val
		node1 := &ListNode{Val: val1}
		node2 := &ListNode{Val: val2}
		if val1 > val2 {
			cur.Next = node2
			list2 = list2.Next
			cur = cur.Next
		} else {
			cur.Next = node1
			list1 = list1.Next
			cur = cur.Next
		}

	}
	return dummy.Next
}

合并K个升序链表

func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
	dummy := &ListNode{Val: -1}
	cur := dummy
	for list1 != nil || list2 != nil {
		if list1 == nil {
			cur.Next = &ListNode{Val: list2.Val}
			cur = cur.Next
			list2 = list2.Next
			continue
		}
		if list2 == nil {
			cur.Next = &ListNode{Val: list1.Val}
			cur = cur.Next
			list1 = list1.Next
			continue
		}
		val1 := list1.Val
		val2 := list2.Val
		node1 := &ListNode{Val: val1}
		node2 := &ListNode{Val: val2}
		if val1 > val2 {
			cur.Next = node2
			list2 = list2.Next
			cur = cur.Next
		} else {
			cur.Next = node1
			list1 = list1.Next
			cur = cur.Next
		}

	}
	return dummy.Next
}

func mergeKLists(lists []*ListNode) *ListNode {
    if len(lists) == 0 {
        return nil
    }
	for len(lists) != 1 {
		node1 := lists[0]
		node2 := lists[1]
		twoLists := mergeTwoLists(node1, node2)
		lists = lists[2:]
		lists = append(lists, twoLists)
	}
	return lists[0]
}

栈&队列

框架

经典例题

用栈实现队列

思路
将一个栈当作输入栈，用于压入 push传入的数据；另一个栈当作输出栈，用于 pop 和 peek 操作。

每次 pop或 peek 时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

class MyQueue {
    Deque<Integer> inStack;
    Deque<Integer> outStack;

    public MyQueue() {
        inStack = new ArrayDeque<Integer>();
        outStack = new ArrayDeque<Integer>();
    }

    public void push(int x) {
        inStack.push(x);
    }

    public int pop() {
        if (outStack.isEmpty()) {
            in2out();
        }
        return outStack.pop();
    }

    public int peek() {
        if (outStack.isEmpty()) {
            in2out();
        }
        return outStack.peek();
    }

    public boolean empty() {
        return inStack.isEmpty() && outStack.isEmpty();
    }

    private void in2out() {
        while (!inStack.isEmpty()) {
            outStack.push(inStack.pop());
        }
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/implement-queue-using-stacks/solutions/632369/yong-zhan-shi-xian-dui-lie-by-leetcode-s-xnb6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

用队列实现栈（将队尾元素调到队头的实现）

// 一个队列实现栈
class MyStack {
    Queue<Integer> queue;

    /** Initialize your data structure here. */
    public MyStack() {
        queue = new LinkedList<Integer>();
    }
    
    /** Push element x onto stack. */
    // 将队尾元素调到队头的实现
    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue.poll();
    }
    
    /** Get the top element. */
    public int top() {
        return queue.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue.isEmpty();
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/implement-stack-using-queues/solutions/432204/yong-dui-lie-shi-xian-zhan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

逆波兰表达式

func evalRPN(tokens []string) int {
  var stack []int
  for _,v :=range tokens{
     num,err:= strconv.Atoi(v)
     if err ==nil {
         stack = append(stack,num)
     }else{
         num1,num2 := stack[len(stack)-1],stack[len(stack)-2]
         stack = stack[:len(stack)-2]
         switch (v){
             case "+":
              sum := num1+num2
              stack = append(stack,sum)
             case "-": 
              diff := num2-num1
              stack = append(stack,diff)
             case "*":
              diff := num2*num1
              stack = append(stack,diff)
            case "/" : 
              diff := num2/num1
              stack = append(stack,diff)
         }
     }
  }
  return stack[0]
}

计算器

1+2*3-4/2-(1+2)*3

基础版】整数加减乘除计算器
https://www.programminghunter.com/article/1993997588/

中缀—递归、双栈、转后缀
只贴一个双栈的

//1-(2+4/2)
//【java版实现链接】https://www.programminghunter.com/article/1993997588/
// 这里为了更多的关注算法本身的实现，输入的字符串就只包含1-9的数字和+-*/()
func Calculate(s string) int {
	var optStack []string
	var numStack []int
	for _, v := range s {
		if v == '+' || v == '-' {
        // 很巧妙的设计--往前多看一步=======================
			for len(optStack) != 0 && (optStack[len(optStack)-1] == "+" || optStack[len(optStack)-1] == "-" || optStack[len(optStack)-1] == "*" || optStack[len(optStack)-1] == "/") {
				optStack, numStack = compute(optStack, numStack)
			}
			optStack = append(optStack, string(v))
		} else if len(optStack) != 0 && (v == '*' || v == '/') {
			for len(optStack) != 0 && (optStack[len(optStack)-1] == "*" || optStack[len(optStack)-1] == "/") {
				optStack, numStack = compute(optStack, numStack)
			}
			optStack = append(optStack, string(v))
		} else if v == '(' {
			optStack = append(optStack, string(v))
		} else if v == ')' {
			for optStack[len(optStack)-1] != "(" {
				optStack, numStack = compute(optStack, numStack)
			}
			optStack = optStack[:len(optStack)-1]
		} else {
			atoi, _ := strconv.Atoi(string(v))
			numStack = append(numStack, atoi)
		}
	}
	for len(optStack) != 0 {
		optStack, numStack = compute(optStack, numStack)
	}
	return numStack[0]
}

// 很巧妙的设计--往前多看一步=======================
func compute(optStack []string, numStack []int) ([]string, []int) {
	num1, num2 := numStack[len(numStack)-2], numStack[len(numStack)-1]
	numStack = numStack[:len(numStack)-1]
	numStack = numStack[:len(numStack)-1]
	optSign := optStack[len(optStack)-1]
	optStack = optStack[:len(optStack)-1]
	switch optSign {
	case "+":
		numStack = append(numStack, num1+num2)
	case "-":
		numStack = append(numStack, num1-num2)
	case "*":
		numStack = append(numStack, num1*num2)
	case "/":
		numStack = append(numStack, num1/num2)
	}
	return optStack, numStack
}

/**
表达式：

符号栈   	数字栈
/			2
+			4
(			2
-			1

遇到）开始不断出栈
*/

计算器

1. 双栈
2. 遇到符号要不要马上触发compute()，还是推迟一步，需要根据上一个符号来决定—往前看一步的思想非常巧妙
   1-4/2+2、1-（4+2/2)

 if (c == '+' || c == '-') {
 //1---值得反复学习借鉴
                while (!operator.isEmpty() && ((operator.peek() == '+') || (operator.peek() == '-')
                        || (operator.peek() == '/') || (operator.peek() == '*'))) {
                    oper(operator, operand);
                }
                operator.push(c);
            } else if (c == '/' || c == '*') {
//2---值得反复学习借鉴
                while (!operator.isEmpty() && ((operator.peek() == '/') || (operator.peek() == '*'))) {
                    oper(operator, operand);
                }
                operator.push(c);

            }
//3---值得反复学习借鉴           
while (!operator.isEmpty()) {
            oper(operator, operand);
            ;
        }

合并K个升序链表（优先队列）

非常好的理解优先队列如何工作的例子

23. 合并K个升序链表(方法1和方法2都是从队列里面取出来（取一个/取两个…）操作完再放回去)

二分法

  static int binarySearch(int[] nums, int target) {
    int left = 0;
    int right = nums.length;
    while (left < right) {
      int mid = (left + right) >>> 1;
      if (target == nums[mid]) {
        return mid;
      } else if (target > nums[mid]) {
        left = mid + 1;
      } else {
        right = mid - 1;
      }
    }
    return -1;
  }

位运算

• 求整数的各位数之和

  //计算位置的数值
  int getSum(int number) {
    int sum = 0;
    while (number > 0) {
      sum += number % 10;
      number /= 10;
    }
    return sum;
  }

• 与（&）、或（|）、异或（^）、⾮（~）、左移（<<）、右移(>>)、⽆符右移(>>>)
  

双指针

1. 从两边向中间（回文字符串）
2. 从中间向两边（盛最多水的容器）
3. 同向从左往右（最长不重复子字符串）

双指针算法详解

图

框架

经典例题

螺旋矩阵

func spiralOrder(matrix [][]int) []int {
	var res []int
	row := len(matrix)
	column := len(matrix[0])
	all := row * column

	//初态--终态---对比----模拟变化的部分
	//边界
	top := 0
	bottom := row - 1
	left := 0
	right := column - 1
	count := 0
	for count < all {  //注意这里不是count==all

        
		for i := left; i <= right && count < all; i++ { //这个限制必须加上，否则元素会被重复计算
			res = append(res, matrix[top][i])
			count++
		}
		top++  //这个设计非常巧妙，这样[1,2,3，4,5,6，7,8,9]边角的3，9就不会被重复计算

		for i := top; i <= bottom && count < all; i++ {
			res = append(res, matrix[i][right])
			count++

		}
		right--

		for i := right; i >= left && count < all; i-- {
			res = append(res, matrix[bottom][i])
			count++
		}
		bottom--

		for i := bottom; i >= top && count < all; i-- {
			res = append(res, matrix[i][left])
			count++
		}
		left++
	}
	return res
}

岛屿数量

func numIslands(grid [][]byte) int {
	row := len(grid)
	column := len(grid[0])
	sum := 0
	for i := 0; i < row; i++ {
		for j := 0; j < column; j++ {
			if grid[i][j] == '1' {
				num := rcs(i, j, grid)
				sum += num
			}
		}
	}
	return sum
}

func rcs(i, j int, grid [][]byte) int {
	if i >= len(grid) || i < 0 || j >= len(grid[0]) || j < 0 || grid[i][j] == '0' || grid[i][j] == '2' {
		return 0
	}
    //这是一个打标签的过程，将相连的1标记成2，并记作一个岛屿，明白这点很重要
	//思考有个过程---抽丝剥茧
	grid[i][j] = '2'  //很经典
	rcs(i+1, j, grid) //向下
	rcs(i, j-1, grid) //向左
	rcs(i, j+1, grid) //向右
	rcs(i-1, j, grid) //向上
    //grid[i][j] = '2'  //不能放在这里
	return 1
}

时间空间优化

java LinkedList中的remove的是先根据值找到节点的引用，然后在删除，时间复杂度O（n）
golang list中的remove是根据节点引用进行删除，时间复杂度O（1）

经典例题

多数元素(选出次数最多的元素：要求O(1)的空间复杂度)

投票算法

最初选举人给自己投一票，往后遍历。支持(相同数)你的人给你投一票，票数加1，反对(不同数)你的人给你减一票，票数减一，当你的票数为零的时候，那你就要更换选举人嘛，然后开始重新投票。

相消思想,消杀，打擂台，相杀

 int majorityElement(int[] nums) {
     int consistant=nums[0];
     int times=1;
     for(int i=1;i<nums.size();i++){
         if(consistant==nums[i]) times++;
         else{
             if(times==0) consistant=nums[i];
             else times--;
         }
     }
     return consistant;
 }

我的灵感来源很简单，就是一个简单事实：如果一个数组有大于一半的数相同，那么任意删去两个不同的数字，新数组还是会有相同的性质。 基于这个事实，就引发了类似 参考这个回答一样的相消思想，然后就出来算法了。

补充

思想

学习数据结构和算法的框架思维

我的刷题心得-如何穷举，如何聪明的穷举

---

东哥的鸡汤：这题你可以不会，但是一定要在力所能及的范围内做到极致！

东哥可以说是算法思想家

所有的算法都只是一种更聪明的遍历(都是在追求如何更简单的遍历，如何更少次数的遍历就能求解出答案)

计算机解决问题其实没有任何奇技淫巧，它唯⼀的解决办法就是穷举，穷举所有可能性。算法设计⽆⾮就是先思考“如何穷举”，然后再追求“如何聪明地穷举”。

列出动态转移⽅程，就是在解决“如何穷举”的问题。之所以说它难，⼀是因 为很多穷举需要递归实现，⼆是因为有的问题本⾝的解空间复杂，不那么容 易穷举完整。 备忘录、DP table 就是在追求“如何聪明地穷举”。⽤空间换时间的思路，是 降低时间复杂度的不⼆法门，除此之外，试问，还能玩出啥花活？

把时间花在寻找问题的方法，而不是寻找问题的合理解释上

以下2点就是我需要恶补的基础知识，掌握了才能通过leedcode题的现象看到本质的东西，才能以不变应万变，不会说题目刷过n遍，但只要过2周就完全不知道了

leedcode上大部分题目有些是思路上难以想到：比如是背包问题的变种，滑动窗口的变种，比如N字形变换…这样的其实看起来很快的：每天浏览搜集个30题没问题

比较难的可能是思路想到了但编码不会：比如排列组合，滑动窗口，背包问题，堆排序，最近最少淘汰，二叉树遍历（关键情况考虑不到位）：通过框架模版可以较好解决

先从简单重要的，能解决部分情况的方案入手—说出你的想法

我写了套框架，把滑动窗口算法变成了默写题
说句题外话，其实有很多人喜欢执着于表象，不喜欢探求问题的本质。比如说有很多人评论我这个框架，说什么散列表速度慢，不如用数组代替散列表；还有很多人喜欢把代码写得特别短小，说我这样代码太多余，影响编译速度，LeetCode 上速度不够快。

我也是服了，算法看的是时间复杂度，你能确保自己的时间复杂度最优就行了。至于 LeetCode 所谓的运行速度，那个都是玄学，只要不是慢的离谱就没啥问题，根本不值得你从编译层面优化，不要舍本逐末……

labuladong 公众号的重点在于算法思想，你把框架思维了然于心套出解法，然后随你再魔改代码好吧，你高兴就好。

编写算法在于写意，把框架写出来，再填充骨肉，尤其像递归

labuladong东哥讲算法

labuladong公众号文章目录

算法秘籍目录

刷题笔记-练习题

杂记

插⼊元素到指定位置：⽆元素复制以及链表群移
插⼊删除频繁的适合⽤链表，查询频繁的适合⽤数组
链表插⼊的时间复杂度为何是O(1)，查询是O(n)…分配的内存空间是不连续的
这⾥说的只是单纯的插⼊操作，不算找到插在哪⼉的时间。也就是说，当你⼿⾥已经有了要插⼊的节点 的前⼀个节点的引⽤，你可以O(1)插⼊。

查找并不属于插⼊和删除操作范围内，你说的情况只能说查找 元素的复杂度是O(n)。 查找完元素之后才开始插⼊或删除，⽽由于链表本身的特性： 插⼊时不⽤移动后续所有节点或者将整个链表拷⻉到新的内存空间

删除时可以⽤下⼀个节点覆盖当前节点，将问题转化成删除下⼀个节点 所以插⼊和删除都是O(1)。

数组插⼊的时间复杂度为何是O(n)，查询是O(1)…分配的内存空间是连续的

数组插⼊元素的时候，⼏乎要对整个数组的元素都进⾏⼀次拷⻉ ArrayList:系统分配连续空间

插⼊/删除元素到指定位置：要把整个数组都往后移动⼀个位置，复杂度为O(n) LinkList:系统随机分配空间

1. 数组去重时间复杂度多少
   3种时间复杂度实现不同类型的无序数组去重O(n²),O(nlogN),O(n)

2. 位图优化空间复杂度的原理是什么
   BitMap的原理以及运用
   Bitmap简介