C++哈希表理论基础

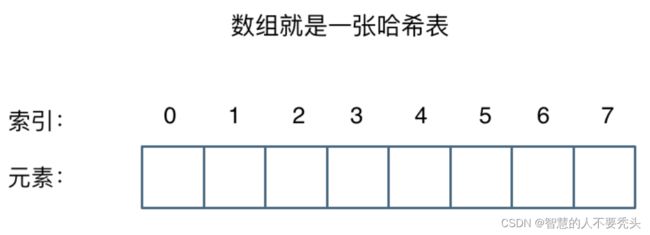
数组：

优点：已知某元素的下标值时，通过下标值的方式获取到数组中对应的元素，这种获取元素的速度是非常快的。

缺点：如果某个元素的下标值未知，而只是知道该元素在数组中，这时我们想要获取该元素就只能对数组进行线性查找，即从头开始遍历，这样的效率是非常低的，如果一个长度为10000的数组，我们需要的元素正好在第10000个，那么我们就要对数组遍历10000次，显然这是不合理的。

所以，为了解决上述数组的不足之处，引入了哈希表的概念。

---

一、什么是哈希表

哈希表，也称散列表，是一种以 键-值(key-value) 存储数据，根据关键码的值而直接进行访问的数据结构。我们只要输入待查找的值即key，即可查找到其对应的值。

二、优秀的哈希函数

秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法，在西方被称作霍纳算法。

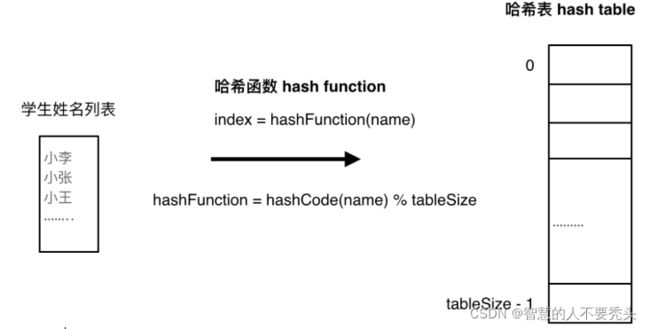
哈希函数如下图所示，通过hashCode把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了。

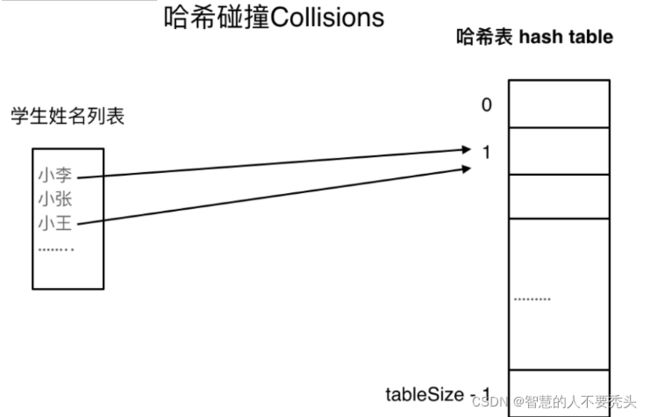
 三、哈希碰撞

 

四、哈希表的优缺点

（1）优点

• 无论数据有多少，处理起来都特别的快
• 能够快速地进行 插入修改元素 、删除元素 、查找元素 等操作

（2）缺点

• 哈希表中的数据是没有顺序的
• 数据不允许重复

五、哈希冲突

一般是有两种方法，即拉链法（链地址法） 和 开放地址法

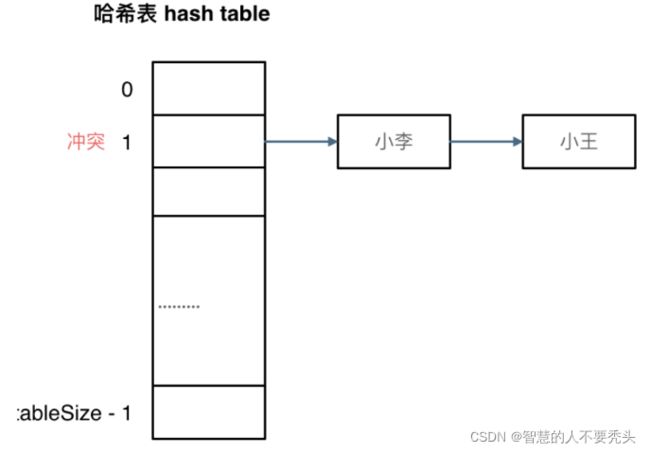
（1）拉链法

10本图书通过哈希化以后存入到长度为10的数组当中，难免有几本书的下标值是相同的，那么我们可以将这两个下标值相同的元素，把发生冲突的元素都被存储在链表中，或存入到一个单独的数组中，然后将该数组存放在他们原本所在数组的下标位置。

 

（2）开放地址法

寻找空白位置插入数据，寻找空白的位置也有三种方法，分别是 线性探测 、二次探测 、再哈希法

1. 线性探测

当某两个元素发生冲突时，将当前索引+1，查看该位置是否为空，是的话就插入数据，否则就继续将索引+1，以此类推……直到插入数据位置。

但这种方法有一个缺点，那就是当数组中连续很长的一个片段都已经插入了数据，此时用线性探测就显得效率没那么高了，因为每次探测的步长都为1，所以这段都已经插入了数据的片段都得进行探测一次，这种现象叫做 聚集。

 

2. 二次探测

二次探测 在线性探测的基础上，将每次探测的步长改为了当前下标值 index + 1² 、index + 2² 、 index + 3² …… 直到找到空白位置插入元素为止。

二次探测 在一定程度上解决了 线性探测 造成的 聚集 问题，但是它却在另一种程度造成了一种聚集，就比如 1² 、2² 、3² …… n² 上的聚集。所以这种方式还是有点不太好

3. 再哈希法

再哈希法 就是再将我们传入的值进行一次 哈希化，获得一个新的探测步数 step，然后按照这个步数进行探测，找到第一个空着的位置插入数据。这在很大的程度上解决了 聚集 的问题。

公认的比较好的哈希函数：step = constant - (key % constant)

其中，constant 是一个自己定的质数常量，且小于数组的容量； key 就是第一次哈希化得到得值。

然后我们再通过这个函数算得的步长来进行查找搜索空位置进行插入即可。

六、哈希表的扩容和减容

填充因子，它表示的是哈希表中的数据个数与哈希表长度的比值。其决定了哈希表的存取数据所需的时间大小。

拉链法：填充因子最小为0，最大为无限大，这是因为该方法是通过在数组中的某个位置插入一个数组用来存储互相冲突的元素，因此，只要有可能，哈希表的长度可以很小，然后数据都存储在内置的数组中，这样填充因子就可以无限大了。

开放地址法，填充因子最小为0，最大只能为1，这是因为开放地址法的实现原理是找哈希表中空位置插入元素，因此哈希表中的数据量不会大于哈希表的长度，从而填充因子最大也只能是1。

把哈希表比作是个教室，如果教室里坐满了人，然后让你从中找出你的朋友，那密密麻麻的，是不是特别不好找，可能会眼花缭乱；但是如果这个教室里只坐了 2/3 或者 1/2 的人，那么人群看起来就没那么密密麻麻，那让你找到你的朋友也许会相对容易一点。

这里我们就将填充因子等于 0.75 作为哈希表扩容的临界点，同时会在后面封装哈希表的时候实现扩容。

当然，填充因子太小也是不合适地，所以我们也会在适当的地方添加减容功能，即将填充因子等于 0.25 作为哈希表减容的临界点。

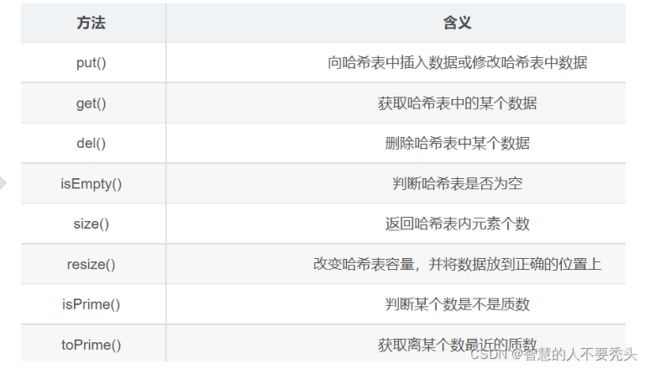
七、哈希表方法

 参考：【数据结构与算法】详解什么是哈希表，并用代码手动实现一个哈希表_零一的博客-CSDN博客>

 <代码随想录>