【LeetCode】—— 二叉树进阶面试题
一、根据二叉树创建字符串LeetCode606题
1.1 题目描述
空节点则用一对空括号 “()” 表示。而且你需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
输入: 二叉树: [1,2,3,4]
1
/ \
2 3
/
4
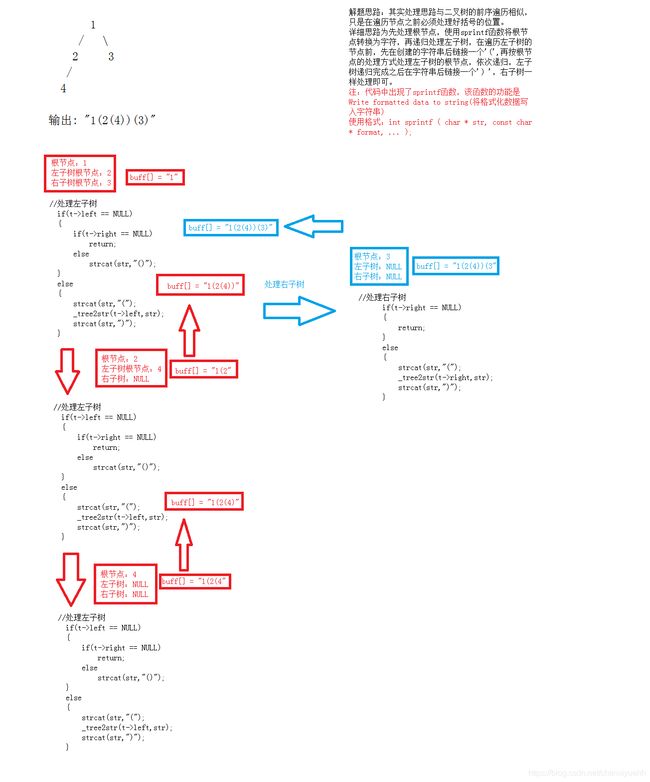
输出: "1(2(4))(3)"
解释: 原本将是“1(2(4)())(3())”,
在你省略所有不必要的空括号对之后,
它将是“1(2(4))(3)”。
示例 2:
输入: 二叉树: [1,2,3,null,4]
1
/ \
2 3
\
4
输出: "1(2()(4))(3)"
解释: 和第一个示例相似,
除了我们不能省略第一个对括号来中断输入和输出之间的一对一映射关系。
1.2 解题思路
- 注:代码中出现了sprintf函数,该函数的功能是Write formatted data to string(将格式化数据写入字符串)
使用格式:int sprintf ( char * str, const char * format, ... );
1.3 代码实现
void _tree2str(struct TreeNode* t,char*str)
{
if(t == NULL)
return;
//处理根节点,将根节点转化为字符
char buff[12];
sprintf(buff,"%d",t->val);
strcat(str,buff);
//处理左子树
if(t->left == NULL)
{
if(t->right == NULL)
return;
else
strcat(str,"()");
}
else
{
strcat(str,"(");
_tree2str(t->left,str);
strcat(str,")");
}
//处理右子树
if(t->right == NULL)
{
return;
}
else
{
strcat(str,"(");
_tree2str(t->right,str);
strcat(str,")");
}
}
char* tree2str(struct TreeNode* t) {
char* str = (char*)malloc(1024*1024);
_tree2str(t,str);
return str;
}
二、二叉树的最近公共祖先节点LeetCode236题
2.1 题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
2.2 解题思路
解题思路是,先创建一个子函数TreeFind函数,来寻找二叉树中是否存在某个节点,且该节点是在二叉树的左子树还是右子树,再将问题分为四种情况讨论
- 第一:若其中一个节点是自己的祖先,直接返回该节点即可
- 第二:若两个节点都在左子树,则将左子树的根节点当做新的根节点继续递归寻找最近公共祖先节点
- 第三:若两个节点都在右子树,则将右子树的根节点当做新的根节点继续递归寻找最近公共祖先节点
- 第四:若两个节点一个在右子树一个在左子树,则直接返回该根节点即可
2.3 代码实现
//若所找节点存在返回1,不在返回0
int TreeFind(struct TreeNode* root,struct TreeNode* node)
{
if(root == NULL)
return 0;
if(root == node)
return 1;
if(TreeFind(root->left,node) == 1)
return 1;
else if(TreeFind(root->right,node) == 1)
return 1;
else
return 0;
}
struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) {
if(root == NULL)
return NULL;
//若其中一个节点是自己的祖先
if(root == p || root == q)
return root;
int pInLeft = TreeFind(root->left,p);
int qInLeft = TreeFind(root->left,q);
//两个节点都在左子树
if(pInLeft == 1 && qInLeft == 1)
return lowestCommonAncestor(root->left,p,q);
//两个节点都在右子树
else if(pInLeft == 0 && qInLeft == 0)
return lowestCommonAncestor(root->right,p,q);
//一个在左子树,一个在右子树
else
return root;
}