机器学习 - 分类 K 最近邻分类算法 K Nearest Neighbor(学习笔记)
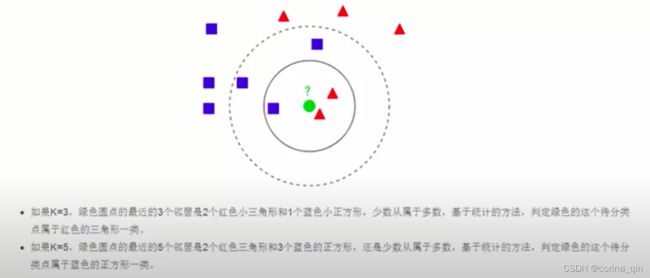
在学习 KNN 算法的过程中,要牢记两个关键词,一个是“少数服从多数”的投票法则(majority-voting),另一个是“距离”,它们是实现 KNN 算法的核心知识。
KNN算法原理
KNN算法本身简单有效,它是一种lazy-learning算法。分类器不需要使用训练集进行训练,训练时间复杂度为0。KNN分类计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为n,那么KNN的分类时间复杂度为O(n)。
KNN 算法简单易于理解,无须估计参数,与训练模型,适合于解决多分类问题、OCR光学模式识别、文本分类等领域。但它的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有很能导致当输入一个新样本时,该样本的 K 个邻居中大容量类的样本占多数,而此时只依照数量的多少去预测未知样本的类型,就会可能增加预测错误概率。此时,我们就可以采用对样本取“权值”的方法来改进。
KNN算法流程
对于未知类别属性数据集中的点:
1.计算已知类别数据集中的点与当前点的距离
2.按照距离依次排序
3.选取与当前点距离最小的K个点
4.确定前K个点所在类别的出现概率
5.返回前K个点出现频率最高的类别作为当前点预测分类
K值减少意味着模型变得复杂,容易受到异常点的影响,容易过拟合;K值增大意味着模型变的简单,容易受到样本均值的问题,容易欠拟合。实际情况,K值一般选择比较小的数值,例如采用交叉验证(简单来说,就是把训练集再分成2组,训练集和验证集)来选择最优的K值。
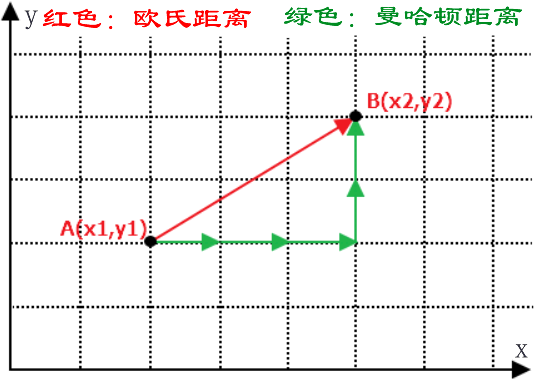
注意:在机器学习中有多种不同的距离公式,下面以计算二维空间 A(x1,y1),B(x2,y2) 两点间的距离为例进行说明,下图展示了如何计算欧式距离和曼哈顿街区距离。
欧氏距离,它表示两点之间最短的距离,其计算公式如下:
曼哈顿街区距离计算公式如下:
![]()
两者区别在于:两点之前线段最短,A 和 B 之间的最短距离就是“欧式距离”,但是在实际情况中,由于受到实际环境因素的影响,我们有时无法按照既定的最短距离行进,比如在一个楼宇众多的小区内,你想从 A 栋达到 B 栋,但是中间隔着其他楼房,因此必须按照街道路线行进(图中绿线),这种距离就被称作“曼哈顿街区距离”。
除上述距离外,还有汉明距离、余弦距离、切比雪夫距离、马氏距离等。在 KNN 算法中较为常用的距离公式是“欧氏距离”。
sklearn实现KNN分类算法
| 类方法 | 说明 |
|---|---|
| KNeighborsClassifier | KNN 算法解决分类问题 |
| KNeighborsRegressor | KNN 算法解决回归问题 |
| RadiusNeighborsClassifier | 基于半径来查找最近邻的分类算法 |
| NearestNeighbors | 基于无监督学习实现KNN算法 |
| KDTree | 无监督学习下基于 KDTree 来查找最近邻的分类算法 |
| BallTree | 无监督学习下基于 BallTree 来查找最近邻的分类算法 |
以下示例通过调用 KNeighborsClassifier 实现 KNN 分类算法。下面对 Sklearn 自带的“红酒数据集”进行 KNN 算法分类预测。最终实现向训练好的模型喂入数据,输出相应的红酒类别,示例代码如下:
#加载红酒数据集
from sklearn.datasets import load_wine
#KNN分类算法
from sklearn.neighbors import KNeighborsClassifier
#分割训练集与测试集
from sklearn.model_selection import train_test_split
#导入numpy
import numpy as np
#加载数据集
wine_dataset=load_wine()
#查看数据集对应的键
print("红酒数据集的键:\n{}".format(wine_dataset.keys()))
print("数据集描述:\n{}".format(wine_dataset['data'].shape))
# data 为数据集数据;target 为样本标签
#分割数据集,比例为 训练集:测试集 = 8:2
# x数据集的特征值 y数据集的标签值 test_size测试集的大小,一般为float
#random_state随机数种子,不同的种子会造成不同的随机采样结果,相同的种子采样结果相同。
X_train,X_test,y_train,y_test=train_test_split(wine_dataset['data'],wine_dataset['target'],test_size=0.2,random_state=0)
#构建knn分类模型,并指定 k 值
KNN=KNeighborsClassifier(n_neighbors=10)
#使用训练集训练模型
KNN.fit(X_train,y_train)
#评估模型的得分
score=KNN.score(X_test,y_test)
print(score)
#给出一组数据对酒进行分类
X_wine_test=np.array([[11.8,4.39,2.39,29,82,2.86,3.53,0.21,2.85,2.8,.75,3.78,490]])
predict_result=KNN.predict(X_wine_test)
print(predict_result)
print("分类结果:{}".format(wine_dataset['target_names'][predict_result]))红酒数据集的键:
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names'])
数据集描述:
(178, 13)
0.7222222222222222
[1]
分类结果:['class_1']
注意:在scikit-learn 中 KNN 算法的 K 值是通过 n_neighbors 参数来调节的,默认值是 5。