Java二叉树进阶面试题讲解
Java二叉树进阶面试题讲解
- 1.二叉树的构建及遍历
- 2.二叉树的分层遍历
- 3.给定一个二叉树, 找到该树中两个指定节点的最近公共祖先
- 4.二叉树搜索树转换成排序双向链表
- 5.根据一棵树的前序遍历与中序遍历构造二叉树
- 6.根据一棵树的中序遍历与后序遍历构造二叉树
- 7.二叉树创建字符串
大家好,我是晓星航。今天为大家带来的是 Java二叉树进阶面试题讲解 的讲解!
1.二叉树的构建及遍历
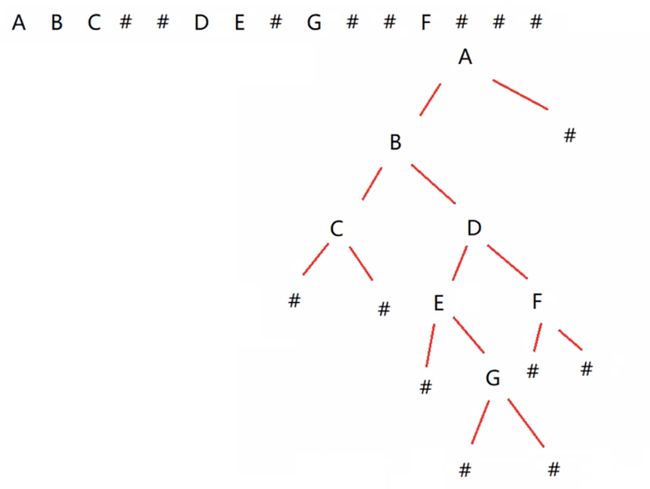
二叉树的构建及遍历。OJ链接


示例图解:
import java.util.*;
class TreeNode {
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static int i = 0;
public static TreeNode createTree(String str) {
TreeNode root = null;
if (str.charAt(i) != '#') {
root = new TreeNode(str.charAt(i));
i++;
root.left = createTree(str);
root.right = createTree(str);
} else {
//遇到# 就是空树
i++;
}
return root;
}
public static void inorder(TreeNode root) {
if (root == null) {
return;
}
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String str = in.nextLine();
TreeNode root = createTree(str);
inorder(root);
}
}
}
思路:根据题目意思:我们的#是null即为空结点的意思,因此我们再使用str.CharAt(i)来遍历我们输入的每一个字符时遇到#就直接i++,即使这一个结点的左结点置为空,如果继续遇到#就继续i++使其右节点也为空,然后返回我们的上一个结点。直到遍历完整个字符串我们的树便算是创建完毕了。

2.二叉树的分层遍历
二叉树的分层遍历 OJ链接


/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();
if (root == null) {
return ret;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();//这个值代表当前行有多少个结点
List<Integer> list = new ArrayList<>();
while (size != 0) {
TreeNode cur = queue.poll();
list.add(cur.val);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
size--;
}
ret.add(list);
}
return ret;
}
}
思路:首先判断树是否为空,为空直接返回链表对象ret,不为空继续往下走,将root根结点添加进入queue队列,并每次拿出一个元素给cur,将cur的值添加到list中,并访问cur的左右结点继续循环直至root树为空,最后返回我们的ret即可。

3.给定一个二叉树, 找到该树中两个指定节点的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。OJ链接
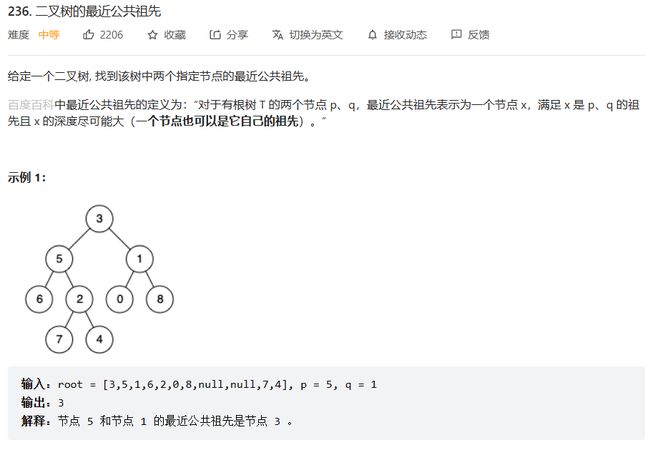

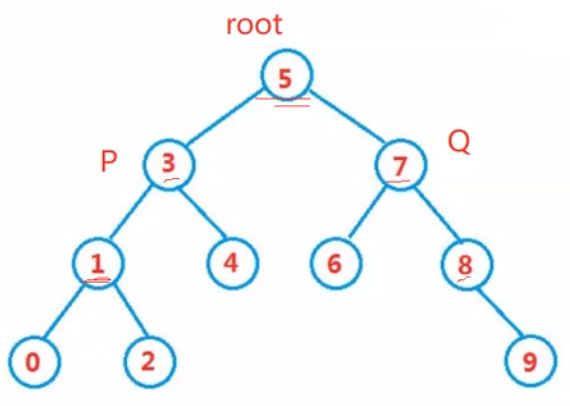
二叉搜索树:根的左边比根小,根的右边比根大 中序遍历的大小是有序的。
思路一:以二叉搜索树为例来讲解此题
1、root == p || root == q 此时的最近公共祖先是root
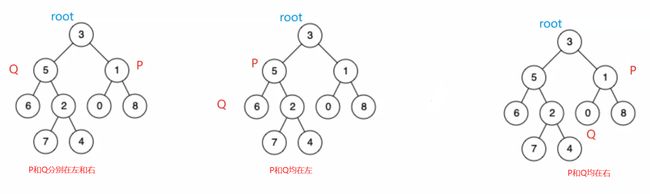
2、p.val < root.val || q.val < root.val p和q都在root的左子树 最近公共祖先在root的左树当中
3、p.val > root.val || q.val > root.val p和q都在root的右子树 最近公共祖先在root的右树当中
4、p.val > root.val && q.val < root.val q和p分别在root的左子树和右子树当中 最近公共祖先就是root
三种情况的图解:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) {
return null;
}
if (root == p || root == q) {
return root;
}
TreeNode leftT = lowestCommonAncestor(root.left,p,q);
TreeNode rightT = lowestCommonAncestor(root.right,p,q);
if (leftT != null && rightT != null) {
return root;
} else if(leftT != null) {
return leftT;
} else if(rightT != null) {
return rightT;
} else {
return null;
}
}
}

当root为3,p为6,q为4时,我们代码运行的逻辑图解:

注:每一次return是返回上一个函数的值,直到第一个递归函数return才是返回我们程序的值。
思路二:假设 这棵二叉树 是使用孩子双亲表示法 表示的
1、用两个栈 存储 路径 — 如何找到从根结点到指定结点的路径
2、求栈的大小
3、计算出两个栈中 多的元素 出差值个元素
4、开始出栈 直到栈顶元素相同 此时就是公共祖先
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
//root:根节点 node:指定的节点 stack:存放指定节点的路径
public boolean getPath (TreeNode root,TreeNode node,Stack<TreeNode> stack) {
if(root == null || node == null) {
return false;
}
stack.push(root);
if(root == node) {
return true;
}
boolean flg = getPath(root.left,node,stack);
if(flg == true) {
return true;
}
flg = getPath(root.right,node,stack);
if(flg == true) {
return true;
}
stack.pop();
return false;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) {
return null;
}
Stack<TreeNode> stack1 = new Stack<>();
getPath(root,p,stack1);
Stack<TreeNode> stack2 = new Stack<>();
getPath(root,q,stack2);
int size1 = stack1.size();
int size2 = stack2.size();
if (size1 > size2) {
int size = size1 - size2;
while (size != 0) {
//出第一个栈里面的元素
stack1.pop();
size--;
}
while(!stack1.isEmpty() && !stack2.isEmpty()) {
//判断地址
if (stack1.peek() == stack2.peek()) {
return stack1.pop();
} else {
stack1.pop();
stack2.pop();
}
}
} else {
int size = size2 - size1;
while (size != 0) {
stack2.pop();
size--;
}
while(!stack1.isEmpty() && !stack2.isEmpty()) {
//判断地址
if (stack1.peek() == stack2.peek()) {
return stack1.pop();
} else {
stack1.pop();
stack2.pop();
}
}
}
return null;
}
}


4.二叉树搜索树转换成排序双向链表
二叉树搜索树转换成排序双向链表OJ链接



思考问题:
1.排序:可以中序遍历这棵二叉搜索树
2.双向链表:如何构建前驱和后续结点
思路:left变为双向链表的前驱
right变为双向链表的后继
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
TreeNode prev = null;
public void inorder (TreeNode pCur) {
if (pCur == null) {
return;
}
inorder(pCur.left);//左
//先判断左 给左节点赋关系
pCur.left = prev;
//在左走完以后 判断prev是否为空 并给右节点赋关系
if (prev != null) {
prev.right = pCur;
}
//在这个节点的左右关系都确定好后将prev变成pCur
prev = pCur;
// System.out.print(pCur.val + " ");
//然后开始进入右节点递归
inorder(pCur.right);//右
}
public TreeNode Convert(TreeNode pRootOfTree) {
if (pRootOfTree == null) {
return null;
}
inorder(pRootOfTree);
TreeNode head = pRootOfTree;
//这个while的作用是找到这棵树的最下的左节点 这个左节点就是我们需要找到的节点
while (head.left != null) {
head = head.left;
}
return head;
}
}
5.根据一棵树的前序遍历与中序遍历构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树 OJ链接


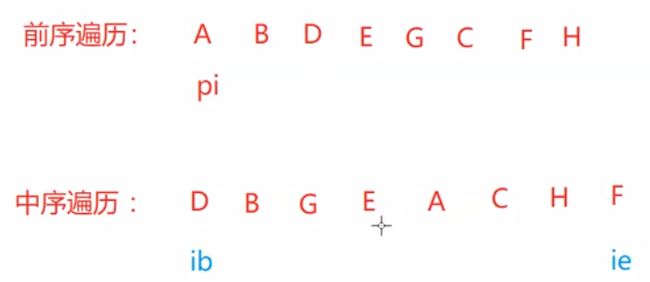
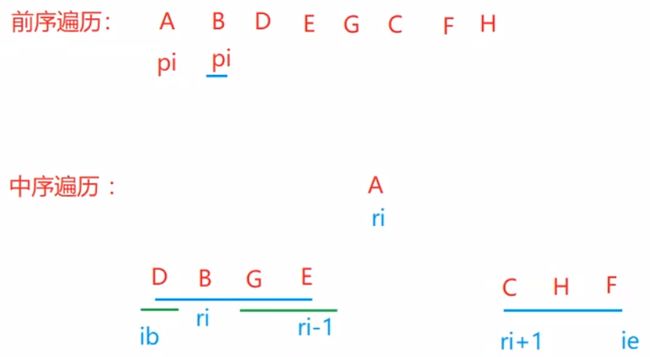
思路:
1、先将pi下标的 元素 创建为root
2、在中序遍历的数组当中,找到当前pi下标的元素,存在的位置。ri
3、root.left = ri - 1;
root.right = ri + 1;
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int preIndex = 0;
public TreeNode creatTreeByPandI(int[] preorder,int[] inorder, int inbegin, int inend) {
if(inbegin > inend) {
//如果满足这个条件 说明 没有左树 或者 右树了
return null;
}
TreeNode root = new TreeNode(preorder[preIndex]);
//找到根在中序遍历的位置
int rootIndex = findIndexOfI(inorder,inbegin,inend,preorder[preIndex]);
if (rootIndex == -1) {
return null;
}
preIndex++;
//分别找到左子树和右子树
root.left = creatTreeByPandI(preorder,inorder,inbegin,rootIndex - 1);
root.right = creatTreeByPandI(preorder,inorder,rootIndex + 1,inend);
return root;
}
private int findIndexOfI(int[] inorder, int inbegin, int inend,int key) {
for (int i = inbegin; i <= inend; i++) {
if (inorder[i] == key) {
return i;
}
}
return -1;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder == null || inorder == null) {
return null;
}
return creatTreeByPandI(preorder,inorder,0,inorder.length-1);
}
}

6.根据一棵树的中序遍历与后序遍历构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树OJ链接


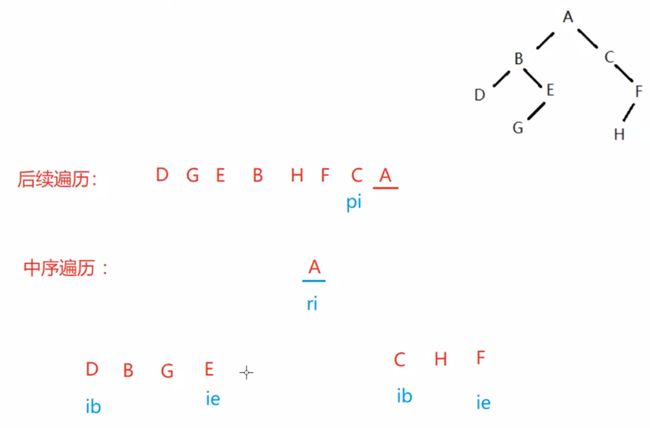
思路:
1、先将pi下标的 元素 创建为root
2、在中序遍历的数组当中,找到当前pi下标的元素,存在的位置。ri
3、先找根,然后在找右子树,最后找左子树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int postIndex = 0;
public TreeNode creatTreeByPandI(int[] inorder,int[] postorder, int inbegin, int inend) {
if(inbegin > inend) {
//如果满足这个条件 说明 没有左树 或者 右树了
return null;
}
TreeNode root = new TreeNode(postorder[postIndex]);
//找到根在中序遍历的位置
int rootIndex = findIndexOfI(inorder,inbegin,inend,postorder[postIndex]);
if (rootIndex == -1) {
return null;
}
postIndex--;
//分别找到右子树和左子树
root.right = creatTreeByPandI(inorder,postorder,rootIndex + 1,inend);
root.left = creatTreeByPandI(inorder,postorder,inbegin,rootIndex - 1);
return root;
}
private int findIndexOfI(int[] inorder, int inbegin, int inend,int key) {
for (int i = inbegin; i <= inend; i++) {
if (inorder[i] == key) {
return i;
}
}
return -1;
}
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (postorder == null || inorder == null) {
return null;
}
postIndex = postorder.length-1;
return creatTreeByPandI(inorder,postorder,0,inorder.length-1);
}
}
7.二叉树创建字符串
二叉树创建字符串OJ链接
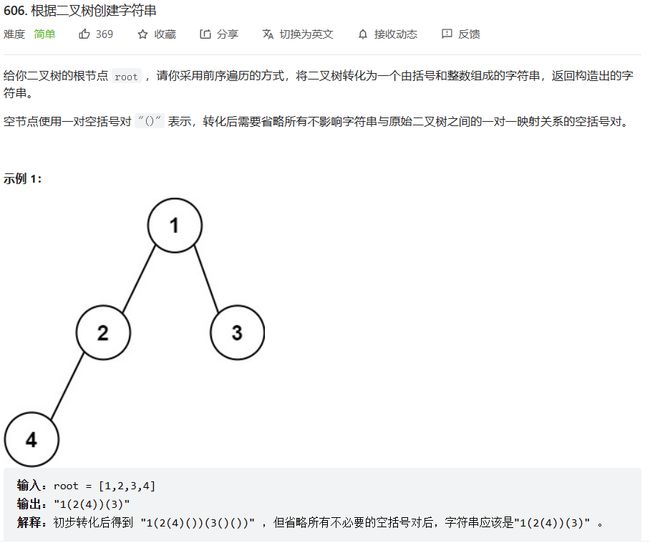
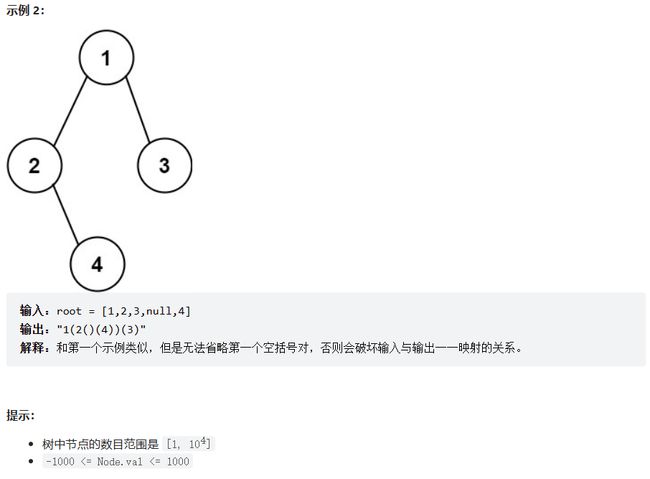
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void treeToString(TreeNode t,StringBuilder sb) {
if (t == null) {
return;
}
sb.append(t.val);
if (t.left != null) {
sb.append("(");
treeToString(t.left,sb);
sb.append(")");
} else {
//t.left == null;
if (t.right == null) {
return;
} else {
sb.append("()");
}
}
if (t.right == null) {
return;
} else {
sb.append("(");
treeToString(t.right,sb);
sb.append(")");
}
}
public String tree2str(TreeNode root) {
if (root == null) {
return null;
}
StringBuilder sb = new StringBuilder();
treeToString(root,sb);
return sb.toString();
}
}
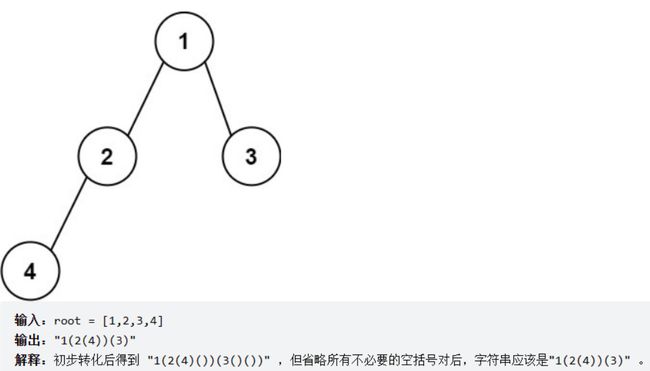
思路:例如上图,我们一直往左,每添加一个元素就加一个"(“,再往右判断如果右也为空我们就添加一个”)“,然后返回到上一个元素,如果右边有元素也是重复之前的操作,添加一个”(“然后继续往后判断,左右为空就添加一个”)“,如果左树为空右树不为空,我们就添加一个”()"。


感谢各位读者的阅读,本文章有任何错误都可以在评论区发表你们的意见,我会对文章进行改正的。如果本文章对你有帮助请动一动你们敏捷的小手点一点赞,你的每一次鼓励都是作者创作的动力哦!