深度学习导航（二）——DNN、RNN、CNN的基本讲解

书接上回

上次讲了下神经网络最简单的定义和基本概念，这次浅谈一下DNN（全连接神经网络或叫深度神经网络）、RNN（循环神经网络）、CNN（卷积神经网络）的基本特征吧，老规矩讲解深度维持入门等级，不涉及具体数学运算而以概念科普为主。

DNN（全连接神经网络或叫深度神经网络）

DNN其实上一节已经提到了，就是多层（“深度”）、互相连通（“全连接”）的神经网络，也是最基础、最不加修饰、最朴实无华的神经网络。还是沿用上一节的图片：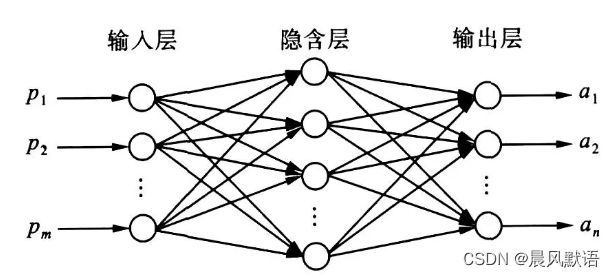
网络即由输入数据、输入层、隐含层（可多层，这幅图隐含层只画了一层）、输出层、输出数据构成，网络的学习方式在上一节的基本概念里已经提过（反向传播是重点），这里不再赘述啦。

DNN作为最初始的网络，提升空间可以说是无限大的，缺点非常明显：
（1）将图像展开为向量会丢失空间信息；
（2）参数过多效率低下，训练困难；
（3）大量的参数很快会导致网络过拟合。

RNN（循环神经网络）

相比DNN，RNN的改进点在于“当前时刻网络的输出不仅取决于此刻的输入数据，还取决于上一时刻”

电气电子或物理出身的同学可能会联想到数字逻辑电路里的一个概念，即时序逻辑电路中的米利型电路：
这里类比理解，存储单元电路的状态相当于是上一时刻的数据，DNN相当于是组合逻辑电路（电路的输出由当前时刻的输入决定），RNN相当于是米利型时序逻辑电路（电路的输出由当前时刻的输入和电路的上一状态共同决定）。

如果没有学过数电，这边可以跳过不看，主要是帮助电专业同学类比理解哒

网络结构简图借用一下大佬的图（出处：https://zhuanlan.zhihu.com/p/30844905，同时强烈推荐这个教程）

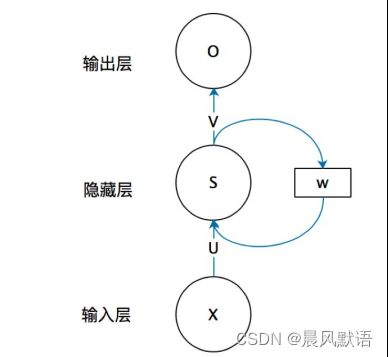
实际上这个所谓的“上一时刻的数据”具体是指上一时刻的隐藏层S的输出乘上权重w，在下一次运算时添加到隐藏层S的输入中。

这里又想提一嘴模电（电专业出身の警觉了属于是），模电里有个电路反馈的概念，其实也有相似之处，但是反馈是上一时刻电路的输出值经过一定处理后与下一时刻的输入信号相加减来起作用的（相当于是O打个箭头出来，经过一个权重w’，再打入输入层X），而这里是上一时刻的中间输出值经过权重影响下一时刻的中间输入值，注意区别记忆（同理没学过模电直接跳过哈）

用数学公式来表达就是：
循环神经网络具有记忆性、参数共享并且图灵完备，因此在对序列的非线性特征进行学习时具有一定优势 。循环神经网络在自然语言处理（Natural Language Processing, NLP），例如语音识别、语言建模、机器翻译等领域有应用，也被用于各类时间序列预报。引入了卷积神经网络（Convolutional Neural Network,CNN）构筑的循环神经网络可以处理包含序列输入的计算机视觉问题。（摘自百度百科）

也即RNN及其衍生网络一般不直接完成计算机视觉或说深度学习相关任务，图像这一块还得CNN。RNN在其他机器学习领域的表现更加突出。RNN有梯度容易爆炸或消失的缺点，具体大家可以自行搜索了解。

最后总结一下RNN，最核心的地方就是：隐藏层S的值不仅和这一次的输入有关，还和上一次隐藏层的值S’有关（准确来说是和之前的每一次输入都有关）。

CNN（卷积神经网络）

CNN的诞生可以说是深度学习领域的一大飞跃。单纯的CNN网络一般用于图像分类任务。

卷积的定义(Convolution)

顾名思义，CNN最大的特点就是“卷积”。大家可能在信号与系统等学科中接触到过卷积（Convolution）,而这里的卷积是指图像卷积，本质当然还是数学运算。这里不可避免地要提一下卷积运算的定义：

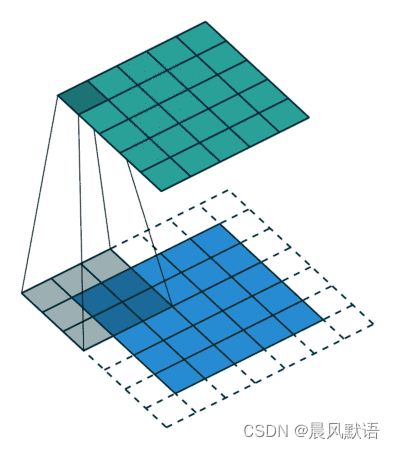
图像可以分为很多个像素点，对于三通道图像每个像素点都由三个数字组成，代表光学三原色红绿蓝的比重，当然BGR和RGB图像的通道顺序不同。这里为了叙述简单先讲解**单通道图像（灰度图）**的卷积，此时图片可以分解为无数多个小方格（像素点），每个小方格是一个数字。

首先我们构造一个卷积核，卷积核就是一个数字宫格，以3×3的卷积核为例（即图中投射下来的灰色阴影宫格），每个格子里也各自放置着一个数字。卷积就是用这个卷积核去扫描输入图像，然后每扫一次3×3的格子，就让对应格子里面的数字相乘，然后相加得到一个数字，这个数字再构成一个小方格作为卷积的第一个输出结果。以此方式不断扫描得到的就是卷积结果：

默认情况下这个扫描的步长是1（可以改变），即下一时刻应该是：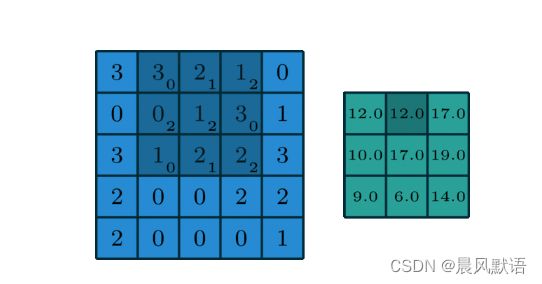
对于三通道或者多通道的情况原理类似：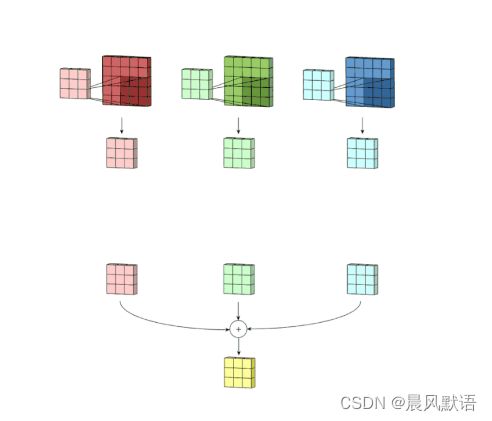
以三通道图为例，此时只是用一个三通道的卷积核分通道进行扫描得到三个结果，再将三个结果里的每个格子对应相加，最后还是得到一个宫格（即结果是单通道图）。当然我也可以设计多个同规模的卷积核，规律一定满足：卷积核的通道数等于输入通道数，卷积核的个数等于输出通道数。

权值共享

此外，大家可能还会听说CNN的“权值共享”概念。权值共享其实就是指在一次卷积操作中，卷积核（又叫过滤器）宫格内的数字（权值，权重）是固定的，扫描的过程中每个扫描块都共用这些固定权重，这就是权值共享。权值共享是理所当然的，对同一图片，同一次卷积，图片的不同扫描区域当然要用相同的权值去乘，否则卷积核还要时刻变化，输入图像不同区域的权值不同还要分开处理，显然会无意义地增加运算量和数据量。

卷积核又叫过滤器，“过滤”过程中，漏斗肯定不能换，否则就是过滤标准在换，过滤的结果也将不明不白。

权值共享有助于模型能学习到不同位置的同一类型特征，也就是卷积网络能很好的适应图像的小范围的平移性，即有较好的平移不变性（比如将输入图像的猫的位置移动之后，同样能够检测到猫的图像）。

Padding机制

细心的同学应该已经发现，卷积的第一幅图中，投射的宫格边缘一圈是用虚线表示的，这一圈其实是额外添加上去的，叫做卷积的Padding机制。

再把这张图拿过来：
为什么要有Padding操作？试想如果不加外围这一圈，那么卷积之后的结果肯定是小于5×5的（结果是3×3，原图是5×5），而CNN网络一般要进行很多次卷积操作，如果这样下去输出的尺寸会越来越小，甚至不够卷积计算，这样肯定是不行的。

而添加外围后（Padding的格子内数字一般是0，防止噪音干扰），卷积的结果仍然是5×5的宫格，保持和输入尺寸一致。除此之外，Padding还有保持图片边缘信息完整等作用。

池化操作（Pooling）

池化层通常接在卷积层后面，引入它的目的就是在保持图片特征的前提下，为了简化卷积层的输出，减少运算的数据量，有效防止过拟合。它只是对窗口范围内的宫格做简单的操作，如求和、求最大值等，再将输出结果传到网络的下一层。

简单的池化一般有平均池化和最大池化：


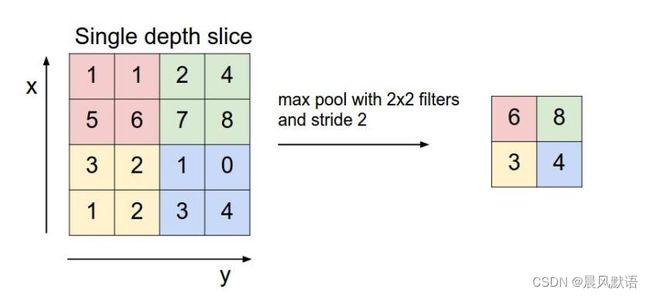
很好理解，和卷积运算相似，池化也有一个固定的窗口大小（图中是2×2），平均池化就是依次求扫描的4个数字的平均值，最大池化就是依次求扫描的4个数字中的最大值。这样很明显输出的数据量大幅减少了。

不过值得注意的是，对于多通道的输入来说，池化和卷积不同，池化就是对每一个通道上都进行这样的操作，最后不需要加在一起，也就是说池化前后的输入输出通道不变（一次池化的窗口唯有一个，而一次卷积的核可以有多个），仅仅改变了特征图的大小。

补充说明，池化属于下采样的范畴，下采样的范围更大些，包含各种缩小（浓缩）图像特征的操作。

局部感受野

局部感受野也是CNN网络的一个特点。

图像的空间联系是局部的，每个神经元不需要对全部的图像做感受，只需要感受局部特征即可，然后在网络深层将这些局部神经元综合起来就可以得到全局的信息了，这样可以减少连接的数目，简化网络参数运算。

也即一个神经元只“看得到”局部的信息，相比每个神经元都读取整个图像而言，实在简化太多了。

全连接层（含Softmax层）

全连接层的架构可以直接理解为DNN。

全连接层，是每一个结点都与上一层的所有结点相连，用来把前边提取到的特征综合起来。由于其全相连的特性，一般全连接层的参数也是最多的。

在经过多轮卷积层和池化层的处理之后，在CNN的最后一般会由1到2个全连接层来给出最后的分类结果。经过几轮卷积层和池化层的处理之后，可以认为图像中的信息已经被抽象成了信息含量更高的特征。我们可以将卷积层和池化层看成自动图像特征提取的过程。在提取完成之后，仍然需要使用全连接层来完成分类任务。

最后一层全连接层的输出值被传递给一个输出，可以采用 softmax逻辑回归（softmax regression）进行分类，该层也可称为 softmax层（softmax layer）。
关于Softmax逻辑回归的具体数学原理，大家可以查阅百度百科，数学推导较为复杂这里不作赘述。

整体网络结构

CNN整体网络结构如上，即多组卷积池化 + 全连接（softmax），一般是用于图像分类任务。

总结

本节主讲DNN、RNN、CNN的相关概念，其中CNN是重要内容，且概念较多较杂，我肯定有疏忽的或者讲错的地方，敬请斧正。

下一节讲解各种RCNN网络的特点，RCNN是第一个成功将深度学习应用到目标检测上的算法。

参考

DNN知乎教程：
https://zhuanlan.zhihu.com/p/104576756

RNN百度百科：
https://baike.baidu.com/item/%E5%BE%AA%E7%8E%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/23199490?fromtitle=RNN&fromid=5707183&fr=aladdin

RNN知乎教程：
https://zhuanlan.zhihu.com/p/30844905

卷积运算和池化操作：
https://blog.csdn.net/weixin_45747759/article/details/122622437?spm=1001.2014.3001.5502

Padding机制：
https://blog.csdn.net/AnneQiQi/article/details/103573917

CNN总体参考：
https://blog.csdn.net/qq_42363032/article/details/108180740

https://blog.csdn.net/weixin_37763870/article/details/103098532

https://blog.csdn.net/weixin_42253689/article/details/109521860

全连接层百度百科：
https://baike.baidu.com/item/%E5%85%A8%E8%BF%9E%E6%8E%A5%E5%B1%82/22689531?fr=aladdin#2

Softmax逻辑回归百度百科：
https://baike.baidu.com/item/softmax%20%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92/22689563?fr=aladdin