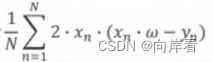Pytorch深度学习笔记（四）梯度向下模型

课程推荐：03.梯度下降算法_哔哩哔哩_bilibili

优化问题：求误差值函数最小的权重w

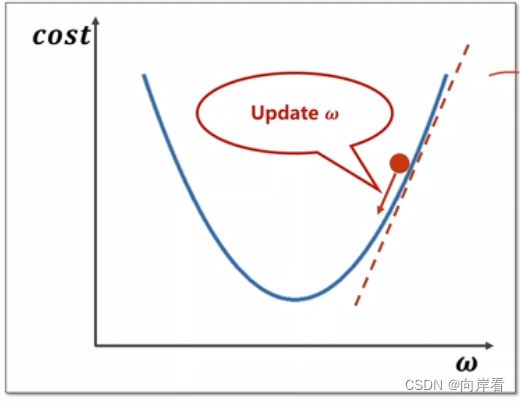
 （1）梯度向下模型思想

在绝大多数的情况下，损失函数是很复杂的（比如逻辑回归），根本无法得到参数估计值的表达式。因此需要一种对大多数函数都适用的方法。这就引出了“梯度算法”。首先，梯度下降(Gradient Descent, GD)，不是一个机器学习算法，而是一种基于搜索的最优化方法。梯度下降法通过导数告诉我们此时此刻某参数应该朝什么方向，以怎样的速度运动，能安全高效降低损失值，朝最小损失值靠拢。

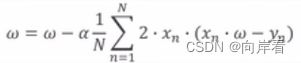
（2）模型公式

更新公式：

注意：  =-，

= ，为误差值函数的导数，也称梯度。为学习率 ，学习率为随机参数，尽量取较小的值。为权重 。

（3）代码实现

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# w初值猜测
w = 1.0

# 预测值函数
def forward(x):
    return x * w

# 求平均误差值
def cost(xs,ys):
    cost = 0
    for x, y in zip(xs, ys):
        # 求预测值
        y_pred = forward(x)
        # 求总误差值
        cost += (y_pred - y) ** 2
        return cost / len(xs)

# 平均导数值函数，也称梯度值函数
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
        # 求梯度值
    return grad / len(xs)

epoch_list = []
cost_list = []

print("训练之前的预测值", 4, forward(4))
# 100轮的训练
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    # 更新w。0.01为学习率,Epoch为训练一次过程
    w -= 0.01 * grad_val
    print('Epoch=', epoch, 'w=', w, 'cost=', cost_val)
    # epoch，cost列表
    epoch_list.append(epoch)
    cost_list.append(cost_val)
print("训练之前的预测值", 4, forward(4))

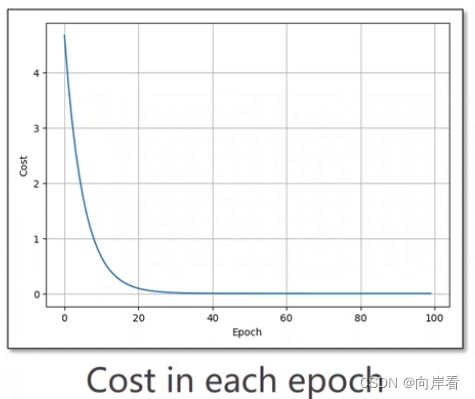
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()

（4） 优化算法：指数加权均值

指数加权均值(exponentially weighted averges)也叫指数加权移动平均，通过它可以来计算局部的平均值，来描述数值的变化趋势。可以使损失曲线变得更加平滑。

 算法公式： 

为优化前的损失值，优化后的损失值，为某个权重。

（5）随机梯度下降

随机梯度下降:每一次更新只采用一个样本来计算梯度，并根据梯度对进行更新。因此可知，对于凸优化问题，每一次更新不能保证是朝着全局最优点前进，但是总体的方法仍然是朝着全局最优的方向前进。相对于批量梯度下降，这种方法单次更新时间更快、存储要求小，且非常适合于增量式更新（假设新的样本源源不断的加入）。对于非凸最优化问题，这种方法通常能够更快的收敛到一个局部最优解。

 随机梯度下降: =- ,更新w的公式每次减去的值由整体样本的梯度变为随机一个样本的梯度。

 代码实现：

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# w初值猜测
w = 1.0

# 预测值函数
def forward(x):
    return x * w

# 求某一误差值
def loss(x,y):
    y_pred = forward(x)
    loss = (y_pred - y) ** 2
    return loss

# 随机梯度值函数
def gradient(x, y):
    # 求随机梯度值
    return 2 * x * (x * w - y)

epoch_list = []
loss_list = []

print("训练之前的预测值", 4, forward(4))
# 100轮的训练
for epoch in range(100):
    for x,y in zip(x_data,y_data):
        # （1）获取随机梯度
        grad = gradient(x, y)
        # （2）更新权重w
        w = w - 0.01*grad
        print("\tgrad", x, y, grad)
        # （3）获取误差值
        l = loss(x, y)
        #
        loss_list.append(l)
        epoch_list.append(epoch)
    print("progress:", epoch,"w=", w, l)

print("训练之前的预测值", 4, forward(4))

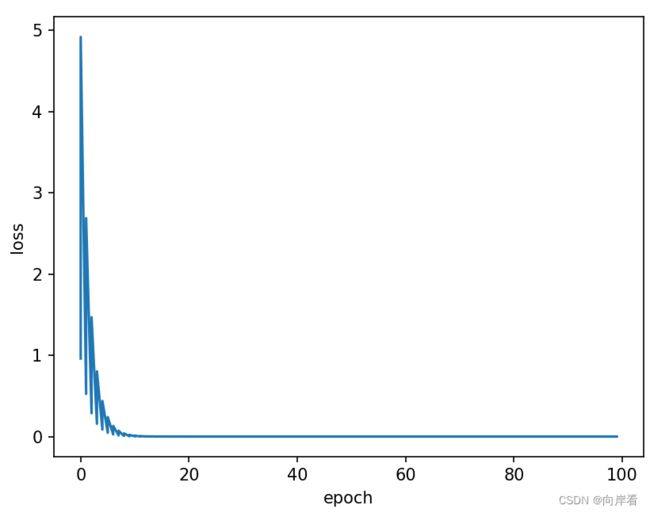
plt.plot(epoch_list,loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

注意：局部最优与鞍点问题，鞍点：梯度为0的点 

非凸函数