Java中常用算法及示例-分治、迭代、递归、递推、动态规划、回溯、穷举、贪心

场景

1、分治算法的基本思想是将一个计算复杂的问题分成规模较小、计算简单的小问题求解，

然后综合各个小问题，得到最终答案。

2、穷举(又称枚举)算法的基本思想是从所有可能的情况中搜索正确的答案。

3、迭代法(Iterative Method) 无法使用公式一次求解，而需要使用重复结构(即循环)重复执行

一段代码来得到答案。

4、递归调用是一个方法在其方法体内调用其自身方法。

5、递推算法是一种理性思维模式的代表，其根据已有的数据和关系，逐步推导而得到结果。

6、动态规划法(Dynamic Programming Algorithm,DPA)类似于分治法，动态规划法的主要做法：

如果一个问题的答案与子问题相关，就能将大问题拆解成各个小问题，

其中与分治法最大的不同是可以让每一个子问题的答案被存储起来，以供下次求解时直接取用。

这样的做法不仅可以减少再次计算的时间，而且可以将这些解组合成大问题的解，可以解决重复计算的问题。

7、回溯法也是枚举法的一种，它的特点就是在搜索过程中寻找问题的解，当发现不满足求解条件时就回溯(返回)，

尝试别的路径，避免无效搜索。

8、贪心法(Greed Method)又称贪婪算法，从某一起点开始，在每一个解决问题的步骤使用贪心原则，

即采用在当前状态下最有利或最优化的选择，不断地改进该解答，持续在每一个步骤中选择最佳的方法，

并且逐步逼近给定的目标，当达到某一个步骤不能再继续前进时，算法就停止，以尽可能快的方法求得更好的解。

注：

博客：
霸道流氓气质的博客_CSDN博客-C#,架构之路,SpringBoot领域博主

实现

1、分治算法

举个例子:要以人工的方式将散落在地上的打印纸从第一个排序整理到第100页，一种方式是逐一捡起稿纸，

按照页码顺序插入到正确的位置。这样的排序和整理的过程比较复杂且浪费时间，可以采用分治法的原理，

先将页码1到10放在一起，页码11到20放到一起，以此列推，将原来的100页分类成10个页码区间，

然后对10堆页码进行整理，最后从页码小到大的分组合并。

代码实例-求最大值

    public static int getMax(int[] a,int begin,int end){
        //元素小于2个，直接找出最大值
        if(end -begin <=1){
            if(a[begin]>a[end])
                return a[begin];
            else
                return a[end];
        //否则进入递归
        }else {
            int center = (begin+end)/2;
            int left = getMax(a,begin,center);
            int right = getMax(a,center,end);
            return  left>right?left:right;
        }
    }

    public static void main(String[] args) {
        int[] a = new int[]{2,5,8,45,65,2,44,532,33};
        System.out.println("最大值:"+getMax(a,0,a.length-1));
    }

2、穷举实例-鸡兔同笼

    static int chichen; //鸡的个数
    static int habbit; //兔的个数

    public static int qiongju(int head,int foot){
        int re,i,j;
        re= 0;
       for(i=0;i<=head;i++){
            j = head - i;
            if(i*2 + j*4 == foot)
            {
                re = 1;
                chichen = i;
                habbit = j;
            }
        }
        return re;
    }

    public static void main(String[] args) {
        int re,head,foot;
        System.out.print("输入头数:");
        Scanner input = new Scanner(System.in);
        head = input.nextInt();
        System.out.print("输入脚数:");
        foot = input.nextInt();
        re = qiongju(head,foot);
        if (re ==1){
            System.out.println("鸡有"+chichen+"只，兔有"+habbit+"只。");
        }else {
            System.out.println("无法求解");
        }
    }

3、迭代实例-for循环计算n!

    public static void main(String[] args) {
        int sum =1;
        for(int i =1;i<8;i++){
            for(int j =i;j>0;j--){
                sum = sum * j;
            }
            System.out.println(i+"!="+sum);
            sum =1;
        }
    }

4、递归调用

    static long fact(int n){
        if(n<=1)
            return 1;
        else
            return n*fact(n-1);
    }

    public static void main(String[] args) {
        int i;
        System.out.print("请输入一个要阶乘的数：");
        Scanner input = new Scanner(System.in);
        i = input.nextInt();
        System.out.println(i+"的阶乘结果为:"+fact(i));
    }

5、递推算法

    1、根据已知结果和关系，求解中间结果。
    2、判断是否达到要求，如果没有达到，则继续根据已知结果和关系求解中间结果；如果满足要求，则表示寻找到一个正确的答案
    数学里面的斐波那契数列是使用递推算法的经典例子
    兔子产仔问题：如果一对两个月大的兔子以后每一个月都可以生一对小兔子，而一对新生的兔子出生两个月后才可以生小兔子。
    也就是说，1月份出生，3月份才可产仔。那么假定一年内没有发生兔子死亡事件，那么一年后共有多少对兔子？

    第一个月：1对兔子
    第二个月：1对兔子
    第三个月：2对兔子
    第四个月：3对兔子
    第五个月：5对兔子

    从第三个月开始，每个月的兔子总对数等于前两个月兔子数的综合

    public static int fibonacci(int n){
        int t1,t2;
        if(n==1 || n ==2){
            return 1;
        }else{
            t1 = fibonacci(n-1);//递归调用
            t2 = fibonacci(n-2);
            return t1+t2;
        }
    }

    public static void main(String[] args) {
        System.out.print("请先输入时间：");
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
        int num = fibonacci(n);
        System.out.println("经过"+n+"月的时间，共繁殖成"+num+"对兔子");
    }

6、动态规划-斐波那契优化

    public static int output[] = new int[1000];

    public static int fib(int n)
    {
        int result;
        result = output[n];
        if(result==0){
            if(n==0)
                return 0;
            if(n==1)
                return 1;
            else
                return (fib(n-1)+fib(n-2));
        }
        output[n] = result;
        return result;
    }

    public static void main(String[] args) {
        int fib = fib(8);
        System.out.println(fib);
    }

7、回溯法示例-老鼠走迷宫

老鼠走迷宫，采用尝试错误的方法找到出口，在走错路时就退回来并把走过的路记下来，避免下次走重复的路，就这样找到出口为止。

老鼠需要遵守以下三个原则:

1、一次只能走一格。

2、遇到墙无法往前走则退回一步，寻找其它路。

3、走过的路不再走第二次。

使用二维数组代表地图，值为1则代表不能通行，值为0则代表可以通行。

假设老鼠从左上角[1][1]进入，从右下角[8][10]出来。

可以使用链表来记录走过的位置，并且将走过的位置所对应的数组元素内容标记为2，然后将这个位置放入堆栈，再进行下一个方向

或路的选择。如果走到死胡同并且还没有抵达终点，就退回到上一个位置，再选择其他的路。由于每次新加入的位置必定会在堆栈的

顶端，因此堆栈顶端指针所指向的方格编号就是当前老鼠的位置，如此重复直至走到迷宫出口为止。

public class HuiSu {
    // 记录老鼠迷宫的行进路径
    public static int ExitX= 8;			//定义出口的X坐标在第8列
    public static int ExitY= 10;		//定义出口的Y坐标在第10行
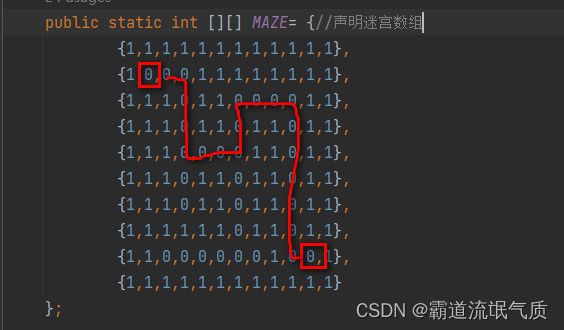
    public static int [][] MAZE= {//声明迷宫数组
            {1,1,1,1,1,1,1,1,1,1,1,1},
            {1,0,0,0,1,1,1,1,1,1,1,1},
            {1,1,1,0,1,1,0,0,0,0,1,1},
            {1,1,1,0,1,1,0,1,1,0,1,1},
            {1,1,1,0,0,0,0,1,1,0,1,1},
            {1,1,1,0,1,1,0,1,1,0,1,1},
            {1,1,1,0,1,1,0,1,1,0,1,1},
            {1,1,1,1,1,1,0,1,1,0,1,1},
            {1,1,0,0,0,0,0,0,1,0,0,1},
            {1,1,1,1,1,1,1,1,1,1,1,1}
    };

    public static void main(String args[]) throws IOException
    {
        int i,j,x,y;
        TraceRecord path=new TraceRecord();
        x=1;
        y=1;
        System.out.print("[迷宫的路径(0的部分)]\n");
        for(i=0;i<10;i++)
        {
            for(j=0;j<12;j++)
                System.out.print(MAZE[i][j]);
            System.out.print("\n");
        }
        while(x<=ExitX&&y<=ExitY)
        {
            MAZE[x][y]=2;
            if(MAZE[x-1][y]==0)
            {
                x -= 1;
                path.insert(x,y);
            }
            else if(MAZE[x+1][y]==0)
            {
                x+=1;
                path.insert(x,y);
            }
            else if(MAZE[x][y-1]==0)
            {
                y-=1;
                path.insert(x,y);
            }
            else if(MAZE[x][y+1]==0)
            {
                y+=1;
                path.insert(x,y);
            }
            else if(chkExit(x,y,ExitX,ExitY)==1)
                break;
            else
            {
                MAZE[x][y]=2;
                path.delete();
                x=path.last.x;
                y=path.last.y;
            }
        }
        System.out.print("[老鼠走过的路径(2的部分)]\n");
        for(i=0;i<10;i++)
        {
            for(j=0;j<12;j++)
                System.out.print(MAZE[i][j]);
            System.out.print("\n");
        }
    }

    public static int chkExit(int x,int y,int ex,int ey)
    {
        if(x==ex&&y==ey)
        {
            if(MAZE[x-1][y]==1||MAZE[x+1][y]==1||MAZE[x][y-1] ==1||MAZE[x][y+1]==2)
                return 1;
            if(MAZE[x-1][y]==1||MAZE[x+1][y]==1||MAZE[x][y-1] ==2||MAZE[x][y+1]==1)
                return 1;
            if(MAZE[x-1][y]==1||MAZE[x+1][y]==2||MAZE[x][y-1] ==1||MAZE[x][y+1]==1)
                return 1;
            if(MAZE[x-1][y]==2||MAZE[x+1][y]==1||MAZE[x][y-1] ==1||MAZE[x][y+1]==1)
                return 1;
        }
        return 0;
    }

    static class Node
    {
        int x;
        int y;
        Node next;
        public Node(int x,int y)
        {
            this.x=x;
            this.y=y;
            this.next=null;
        }
    }
    static class TraceRecord
    {
        public Node first;
        public Node last;
        public boolean isEmpty()
        {
            return first==null;
        }
        public void insert(int x,int y)
        {
            Node newNode=new Node(x,y);
            if(this.isEmpty())
            {
                first=newNode;
                last=newNode;
            }
            else
            {
                last.next=newNode;
                last=newNode;
            }
        }

        void delete()
        {
            Node newNode;
            if(this.isEmpty())
            {
                System.out.print("[队列已经空了]\n");
                return;
            }
            newNode=first;
            while(newNode.next!=last)
                newNode=newNode.next;
            newNode.next=last.next;
            last=newNode;

        }
    }
}

即迷宫路线如下

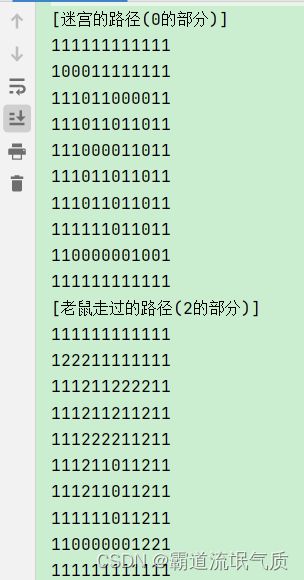
运行结果

8、贪心算法示例-零钱最少找零

    public static void greedMoney(int money){
        System.out.println("需要找零:"+money);
        int[] moneyLevel = {1,5,10,20,50,100};
        for(int i =moneyLevel.length -1;i>=0;i--){
            int num = money/moneyLevel[i];
            int mod = money % moneyLevel[i];
            money = mod;
            if(num>0)
                System.out.println("需要"+num+"张"+moneyLevel[i]+"块");
        }
    }

    public static void main(String[] args) {
        greedMoney(1562);
    }

    //输出结果:
    //需要找零:1562
    //需要15张100块
    //需要1张50块
    //需要1张10块
    //需要2张1块

如果不限制纸币的金额，那这种情况还适合用贪心算法么。

 比如1元，2元，3元，4元，8元，15元的纸币，用来支付K元，至少多少张纸币？

经我们分析，这种情况是不适合用贪心算法的，因为我们上面提供的贪心策略不是最优解。

比如，纸币1元，5元，6元，要支付10元的话，按照上面的算法，至少需要1张6元的，4张1元的，而实际上最优的应该是2张5元的。

所以贪心算法是一种在某种范围内，局部最优的算法。