分治算法,动态规划算法和贪心算法的区别和联系

分治算法,动态规划算法和贪心算法的区别和联系

(一)分治算法

分治算法为什么叫分治算法?

分治这个名字可以分成两部: 第一部分是分,表示把一个原问题分解成很多个小问题,逐个解决; 第二部分是治, 表示把得到的子问题的解再合起来,得到原问题的解.

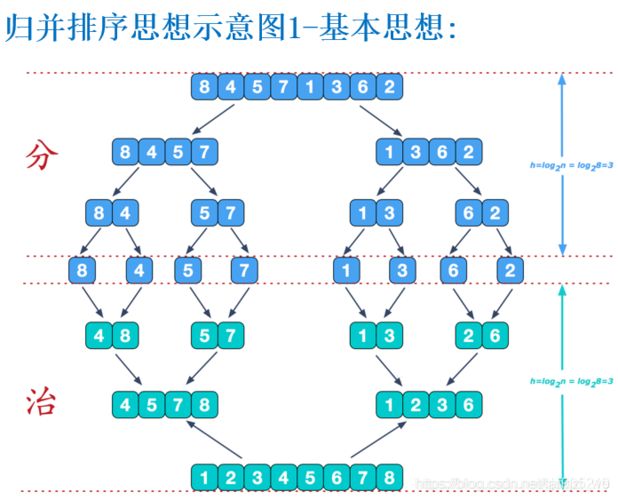
我们以归并排序为例子,来解释分治算法.

我们要对一整个数组排序,我们不妨可以对数组的左半边排序,再对右半边排序,对于左右半边的数组来说,我们仍然对其分成左右两半排序,以此类推,最后分的不能再分的时候,我们对最终得到的子问题进行解决,再把子问题的解一层一层地合并,最后得到完整的数组.

下面是归并排序算法的代码:

#include 
#include 
using namespace std;
const int N = 100010;
int arr[N], tmp[N];//tmp数组是临时数组,详细见归并排序内部

void merge_sort(int arr[], int l, int r)
{
    if(l == r)  return ;//表示子问题已经不能再分解了开始返回
    
    //1.把整个数组划分成左右两边
    int mid = l + r >> 1;
    //2.对两边的数组分别排序
    merge_sort(arr, l, mid), merge_sort(arr, mid + 1, r);
    //3.利用双指针算法将两边排好序的数组放到新的数组中,再把新的数组中的每个元素放回到原数组中
    int i = l, j = mid + 1, k = 0;
    while(i <= mid && j <= r)
    {
        if(arr[i] <= arr[j])    tmp[k ++] = arr[i ++];
        else    tmp[k ++] = arr[j ++];
    }
    while(i <= mid) tmp[k ++] = arr[i ++];
    while(j <= r)   tmp[k ++] = arr[j ++];
    
    for(int i = l, j = 0; i <= r; i ++, j ++ )  arr[i] = tmp[j];
}

int main()
{
    int n;//表示数组元素的个数
    cin >> n;
    
    for(int i = 0; i < n; i ++ )    cin >> arr[i];
    
    merge_sort(arr, 0, n - 1);
    
    //输出数组
    for(int i = 0; i < n; i ++ )    cout << arr[i] << ' ';
    return 0;
}

我们观察分治算法,会发现分治算法有两个个特点:

1.分治算法每次分解出来的子问题是互相独立,不互相影响的.每个子问题都是独立地被求解.

2.分治算法是自顶而下求解的,什么是自顶而下和自底而上呢?

我们举个生动形象的例子:

自底而上:在数学课上,小明通过三角尺发现了一个两条直角边为3,4斜边为5的直角三角形的刚好可以构成3^2 + 4 ^ 2 = 5 ^ 2的等式,这时,数学老师讲了勾股定理,就算直角三角形两条直角边的平方之和等于斜边的平方.

自顶而下:数学老师告诉小明勾股定理,小明通过三角尺发现了3^2 + 4 ^ 2 = 5 ^ 2的等式.

说白了,自底而上是从具体问题分析到抽象问题,也就是从小问题开始求解,一直推广到大问题的求解;自顶而下则相反,是从抽象的问题入手逐渐解决具体的问题,也就是把大问题化小,最后解决小问题.

在说完了分治算法的特点以后,我们再来看一道"家喻户晓"的题目

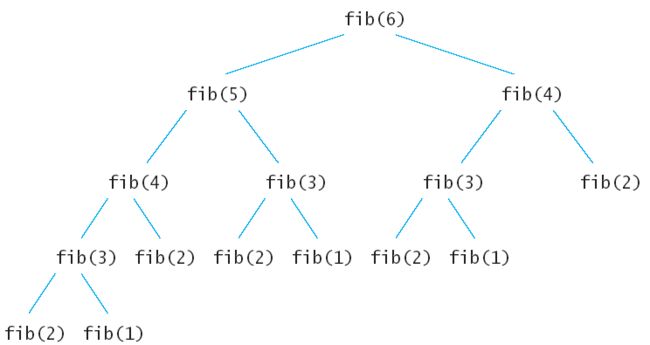
斐波那契数列

即f(n) = f(n - 1) + f(n - 2),我们假设前面的两项f(1), f(2)是1 和 1,我们用分治算法来解决这道问题:

代码实现:

int fibonacci(int n)
{
	if(n <= 0)	return 0;
    if(n <= 2)	return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

我们可以发现,用分治算法来求解斐波那契数列是效率低下的,因为有些子问题被重复求解了很多次,比如f(2)就被求解了5次,f(3)被求解了3次,其实这也是分治算法的特点导致的,正因为分治算法在计算每个子问题的时候是独立的,所以每个子问题被重复求解了,子问题"自身是不知情的".

那么有没有一种更好的方法,来避免子问题被重复求解呢?有,答案就是我们即将讲解的动态规划问题.

(二)动态规划算法

**动态规划算法为什么叫动态规划算法?**实际上,动态规划名字的由来本身是历史性的因素多一些,跟本身的特殊性关系比较小.https://en.wikipedia.org/wiki/Dynamic_programming#History在这里我就不过多赘述了.

动态规划和分治算法的差别:动态规划跟分治算法很相似,都是将大问题拆分成小问题逐个击破.

1.动态规划的子问题并不是互相独立,是有交集的.

2.动态规划多数都是自底而上来求解问题的,先解决小问题,再由小问题解决大问题.(即由之前存在过的状态推导出后面的状态)

3.动态规划会将解决过的子问题的结果记忆起来,用于求解更大的问题或者,遇到相同的子问题时不用再次计算,直接在使用记忆的结果即可.

可能干说概念有点枯燥,有点难以理解,我们仍然以刚才的那道斐波那契数列问题为例,看一下动态规划是怎么优化解法的.

int fibonacci(int n)
{
	if(n <= 0)	return n;
	int [] Memo = new int[n + 1];
	Memo[0] = 0;	Memo[1] = 1;
	for(int i = 2; i <= n; i ++ )	Memo[i] = Memo[i - 1] + Memo[i - 2];//从小问题到大问题逐步解决,由先前的状态退出后面的状态
	return Memo[n];
}
//其实这个代码可以利用滚动数组继续优化,但是这不是我们这篇文章的重点,要了解更多有关动态规划的知识,
//可以在b站上搜背包九讲

与分治算法不同,在用动态规划解决问题的时候,是用迭代来解决问题的,说白了就是循环啦,为什么不用递归来解决问题呢?其实这跟递归的特性有关,递归一般适合将大问题拆成小问题,要是将小问题累积成大问题可能有些麻烦;用迭代的话,可以通过调整顺序,让问题从小到大一步步得到解决.

当然,动态规划也可以通过递归的方式解决,比如记忆化搜索问题,这里限于篇幅,就不多说啦.

动态规划问题常常被用于求解全局最优解的问题,这是因为他的特性,他可以记忆所有子问题的解,那么基于这个特性,动态规划算法可以在解决子问题的同时,不断更新当前的最优解,最后得到全局的最优解.当然,前提是这个问题是这个问题必须具有最优子结构和无后效性.

1.最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，那我们也可以理解为，后面阶段的状态可以通过前面状态推导出来。

2.无后效性，有两层含义，第一层含义是，在推导后面阶段状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么一步步推导出来的。第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。

(三)贪心算法

**贪心算法为什么叫贪心算法?**在日常的学习中,我们要平衡学习和睡觉的时间,短时间高强度的学习可以提高成绩,但在长期看来会使得学习效率下降,但是在贪心算法看来,我们无需兼顾全局,只要取得当前最优就行.即在解决问题时,不断地求局部最优解,最后合并成一个大问题的解.

在贪心算法使用之前,我们需要知道算法的使用条件,由于贪心算法的最终解是由各个局部最优解构成的,所以,必须保证自己制定的贪心策略是正确的(即满足每个局部最优解都是全局最优解的组成部分),才可以用贪心算法.

我们再举一个例子:

合并果子

对于这个问题,我们先制定贪心策略,在这里再提一嘴,对于贪心问题,我们的做法通常都是先猜后证, 即先凭直觉猜出结论,再证明他.

我们先将最轻的两种果子合并成一堆,再合并剩下来最轻的两堆,以此类推,最终消耗的体力值是最小的.

下面是贪心策略的证明:

代码实现:

#include 
#include 
#include 
using namespace std;

int main()
{
    int n;	//果子的数量
    scanf("%d", &n);
    int k = n;
    priority_queue, greater> heap;//用小根堆存储果子,将会对果子自动排序
    while(k -- )
    {
        int a;
        scanf("%d", &a);
        heap.push(a);
    }
    int res = 0;
    for(int i = 0; i < n - 1; i ++ )
    {
        int a = heap.top(); heap.pop();
        int b = heap.top(); heap.pop();
        res += a + b;	//记录合并两堆最轻的果子需要的体力值
        heap.push(a + b);   
    }
    
    cout << res << '\n';
    
    return 0;
}

我们可以发现贪心算法跟动态规划算法又有了很大的差别,贪心算法的时间复杂度要低于动态规划的时间复杂度.这是因为**贪心算法每次将问题拆分的时候,都只拆成一个子问题,**我们只对这个子问题进行求解就行,这是贪心算法的特点,不过这个特点很依赖这个问题本身的特性,也就是这个问题到底能不能这样拆解,这样问题又回到了我们之前提到的局部最优解是不是全局最优解的组成部分这个问题了,要解决这个问题,依靠的是逻辑严密的证明.

最后,我们用三句话,分别概括分治,贪心和动态规划:

1.分治:将问题域划分为多个子问题域，然后都这些问题域分别求解后，在将所得的所有解融合。

2.贪心:将问题域划分为一个子问题域，然后都这些问题域分别求解后，在将所得的所有解融合。

3.动态规划:将计算过程中的结果保存下来重复使用，避免无必要的重复计算。

题,依靠的是逻辑严密的证明.

最后,我们用三句话,分别概括分治,贪心和动态规划:

1.分治:将问题域划分为多个子问题域，然后都这些问题域分别求解后，在将所得的所有解融合。

2.贪心:将问题域划分为一个子问题域，然后都这些问题域分别求解后，在将所得的所有解融合。

3.动态规划:将计算过程中的结果保存下来重复使用，避免无必要的重复计算。