S-function入门及案例详解(4)——S-function进阶案例之连续/离散状态空间表达式的S-function实现
目录
- 一、连续系统的状态空间表达式
-
- 1.1 案例描述
- 1.2 案例详解
- 1.3 输出波形
- 二、离散系统的状态空间表达式
-
- 2.1 案例描述
- 2.2 案例详解
- 2.3 输出波形
- 三、离散系统的状态空间表达式(2)
-
- 3.1 案例描述
- 3.2 案例详解
- 3.3 输出波形
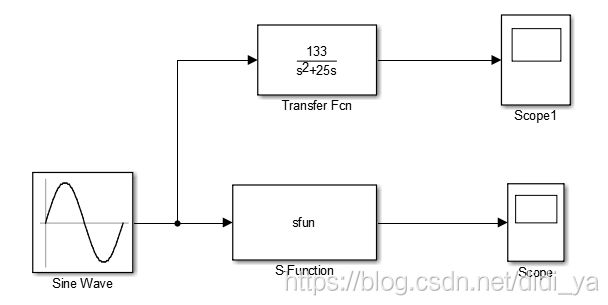
一、连续系统的状态空间表达式
1.1 案例描述
给定二阶传递函数 G ( s ) = 133 s 2 + 25 s G(s)=\frac{133}{s^2+25s} G(s)=s2+25s133,及其状态空间表达式:
x ˙ = ( 0 − 1 0 − 25 ) x + ( 0 133 ) u \dot{x}=\left( \begin{array}{lcr} 0 & -1 \\ 0 & -25 \\ \end{array} \right)x+ \left( \begin{array}{lcr} 0 \\ 133 \end{array} \right)u x˙=(00−1−25)x+(0133)u
y = ( 1 0 ) x y=\left( \begin{array}{lcr} 1 & 0\\ \end{array} \right)x y=(10)x
用s-function表示。
1.2 案例详解
步骤1.可以修改sfuntmpl函数的名称(这里修改为sfun)
function [sys,x0,str,ts,simStateCompliance] = sfun(t,x,u,flag)
步骤2.基本参数初始化
两个连续状态数,一个输出,一个输入,输入和输出没有直接联系
因此,设置相应属性:
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
初始化x0:
x0 = [0 0];
步骤3.设置mdlDerivatives函数
连续状态的导数
function sys=mdlDerivatives(t,x,u)
sys(1) = x(2);
sys(2)=-25*x(2)+133*u;
步骤4.设置mdlOutputs函数
输出函数代码如下:
function sys=mdlUpdate(t,x,u)
sys = x(1);
1.3 输出波形
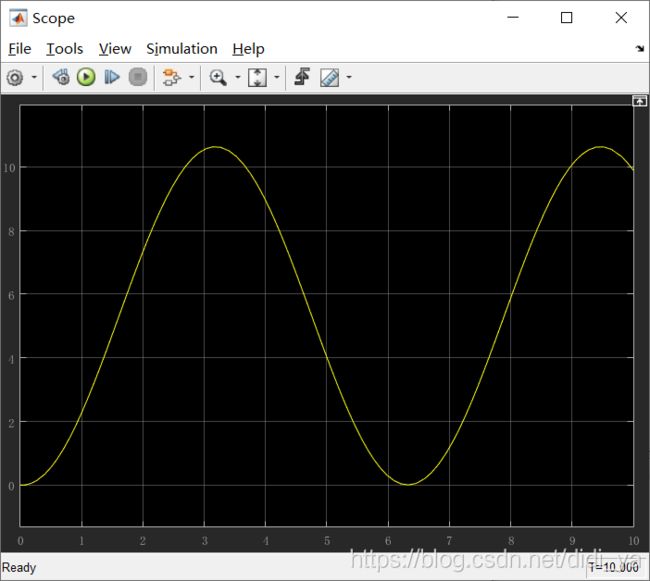
运行发现,二者输出波形相同,说明s-function编写正确!
二、离散系统的状态空间表达式
2.1 案例描述
用S-function实现下面的离散系统:
x ( k + 1 ) = A x ( k ) + B u ( k ) x(k+1)=Ax(k)+Bu(k) x(k+1)=Ax(k)+Bu(k)
y ( k ) = C x ( k ) + D u ( k ) y(k)=Cx(k)+Du(k) y(k)=Cx(k)+Du(k)
其中 A = [ − 1 − 0.5 1 0 ] A=\left[ \begin{array}{lcr} -1 & -0.5 \\ 1 & 0 \end{array} \right] A=[−11−0.50], B = [ − 2.5 4.2 ] B=\left[ \begin{array}{lcr} -2.5 \\ 4.2 \end{array} \right] B=[−2.54.2], C = [ 0 2 0 7 ] C=\left[ \begin{array}{lcr} 0 & 2 \\ 0 & 7 \end{array} \right] C=[0027], D = [ − 0.8 0 ] D=\left[ \begin{array}{lcr} -0.8 \\ 0 \end{array} \right] D=[−0.80]
2.2 案例详解
步骤1.可以修改sfuntmpl函数的名称(这里修改为fuzhi),然后在主函数主体中输入矩阵A,B,C,D的值:
function [sys,x0,str,ts,simStateCompliance] = fuzhi(t,x,u,flag)
A=[-1,-0.5;1,0];
B=[-2.5;4.2];
C=[0,2;0,7];
D=[-0.8;0];
接着,设置case里的所有函数参数:
case 2,
sys=mdlUpdate(t,x,u,A,B);
case 3,
sys=mdlOutputs(t,x,u,C,D);
步骤2.基本参数初始化
离散状态变量个数为2,2个输出,1个输入,输入和输出有直接联系
因此,设置相应属性:
sizes.NumContStates = 0;
sizes.NumDiscStates = 2;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
初始状态设置为[1,1],采样时间设置为0.1s:
x0 = [1 1];%初始状态为[1,1]
ts = [0.1 0];%采样时间为0.1s
步骤3.设置mdlUpdate函数
function sys=mdlUpdate(t,x,u,A,B)
sys = A*x+B*u;
步骤4.设置mdlOutputs函数
输出函数代码如下:
function sys=mdlOutputs(t,x,u,C,D)
sys = C*x+D*u;
2.3 输出波形
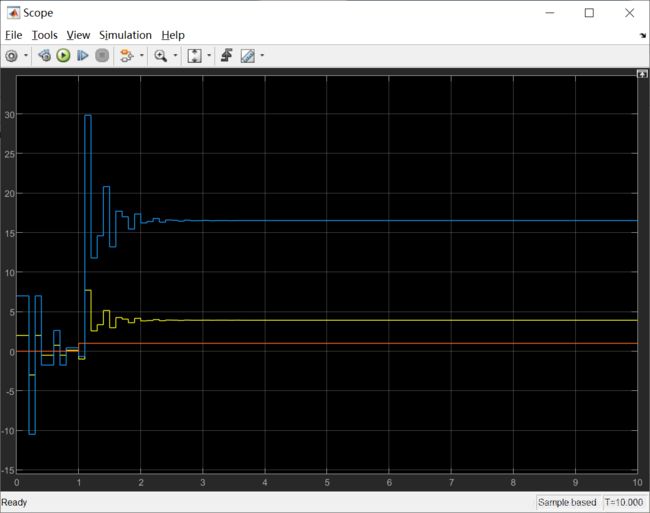
仿真结果如上图所示,黄色曲线为输入阶跃信号,蓝色曲线和红色曲线分别为两个输出变量。
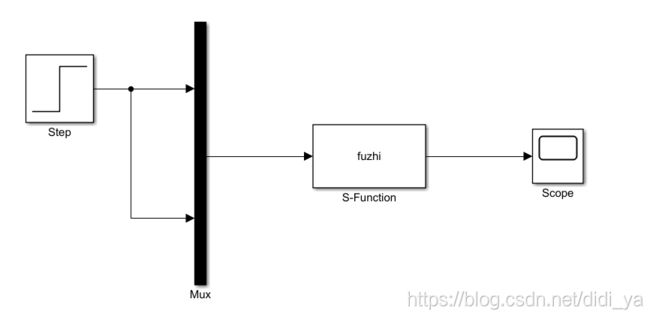
三、离散系统的状态空间表达式(2)
3.1 案例描述
用S-function实现下面的离散系统:
x ( k + 1 ) = A x ( k ) + B u ( k ) x(k+1)=Ax(k)+Bu(k) x(k+1)=Ax(k)+Bu(k)
y ( k ) = C x ( k ) y(k)=Cx(k) y(k)=Cx(k)
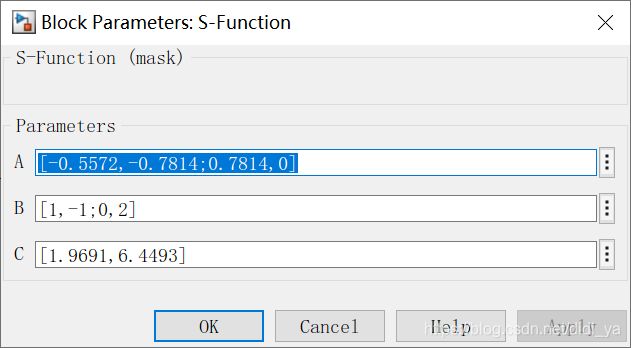
其中 A = [ − 0.5572 − 0.7814 0.7814 0 ] A=\left[ \begin{array}{lcr} -0.5572 & -0.7814 \\ 0.7814 & 0 \end{array} \right] A=[−0.55720.7814−0.78140], B = [ 1 − 1 0 2 ] B=\left[ \begin{array}{lcr} 1 &-1 \\ 0 &2 \end{array} \right] B=[10−12], C = [ 1.9691 6.4493 ] C=\left[ \begin{array}{lcr} 1.9691 & 6.4493 \end{array} \right] C=[1.96916.4493]
3.2 案例详解
步骤1.可以修改sfuntmpl函数的名称(这里修改为fuzhi),并在括号内增加输入参数A,B,C:
function [sys,x0,str,ts,simStateCompliance] = fuzhi(t,x,u,flag,A,B,C)
接着,设置case里的所有函数参数:
case 2,
sys=mdlUpdate(t,x,u,A,B);
case 3,
sys=mdlOutputs(t,x,u,C);
步骤2.基本参数初始化
离散状态变量个数为2,1个输出,2个输入,输入和输出没有直接联系
因此,设置相应属性:
sizes.NumContStates = 0;
sizes.NumDiscStates = 2;
sizes.NumOutputs = 1;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
初始状态设置为[0,0]:
x0 = [0 0];
ts = [0 0];
步骤3.设置mdlUpdate函数
function sys=mdlUpdate(t,x,u,A,B)
sys = A*x+B*u;
步骤4.设置mdlOutputs函数
输出函数代码如下:
function sys=mdlOutputs(t,x,u,C)
sys = C*x;
步骤6.“Create Mask”,创建A,B,C第三个mask:
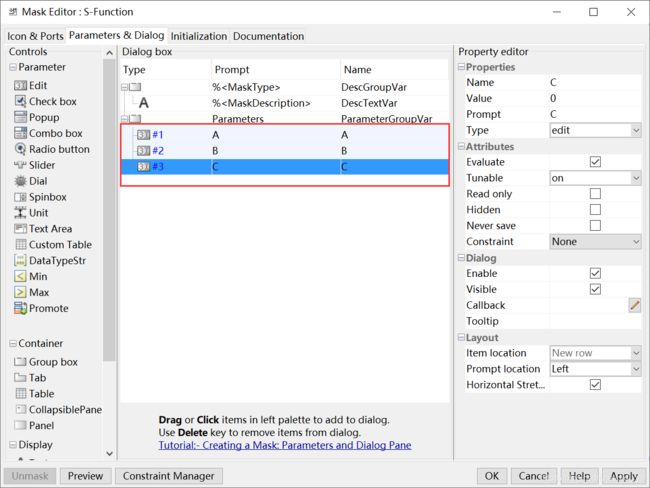
步骤7.右击“Block Parameters”,设置参数,将s-function的参数改为如下形式:
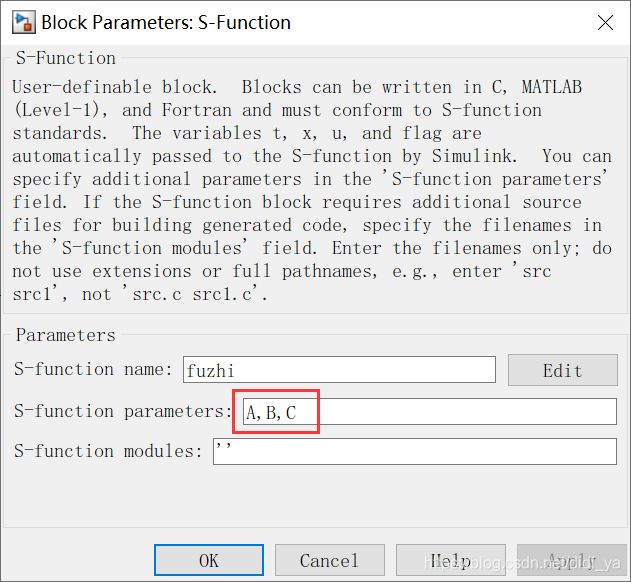
步骤8.双击S-function,输入A,B,C的基本内容:
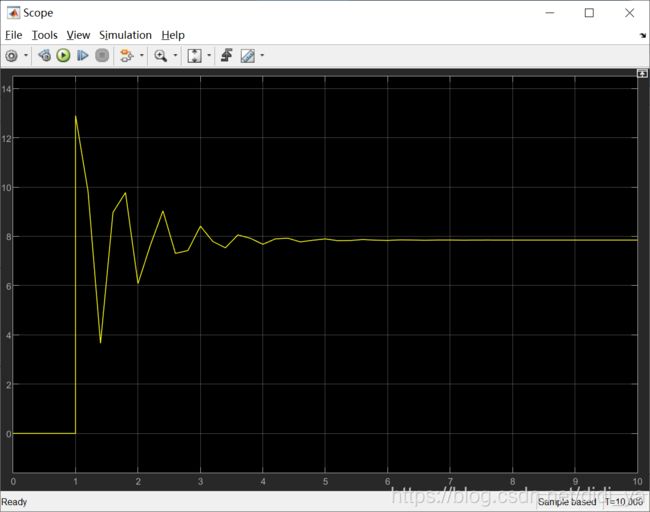
3.3 输出波形
当然,上述S-function中也可以不使用参数列表传递状态方程的参数A,B,C,而使用全局变量在各个子函数中声明,同样也能达到互传的效果,但并不推荐这样做,理由有二:
①全局变量会破坏模块化设计,增加模块之间的耦合性。当系统复杂之后,依赖全局变量过多,会造成难以管理的混乱局面。
②不出现多次global声明,代码看起来清爽简约并充分发挥了S函数的作用。
ok,以上便是全部内容了,如果对你有所帮助,记得点个赞哟~
往期文章:
1. S-function入门及案例详解(1)——S-function基础介绍及基本案例
2. S-function入门及案例详解(2)——S-function基本案例介绍
3. S-function入门及案例详解(3)——S-function进阶案例