线性回归python实现详解(附公式推导)
目录
-
- 1线性回归
-
- 1.1简单线性回归
- 1.2 多元线性回归的正规方程解
- 1.3 使用梯度下降求解多元线性回归
- 1.4 sklearn中的线性回归模型
1线性回归
1.1简单线性回归
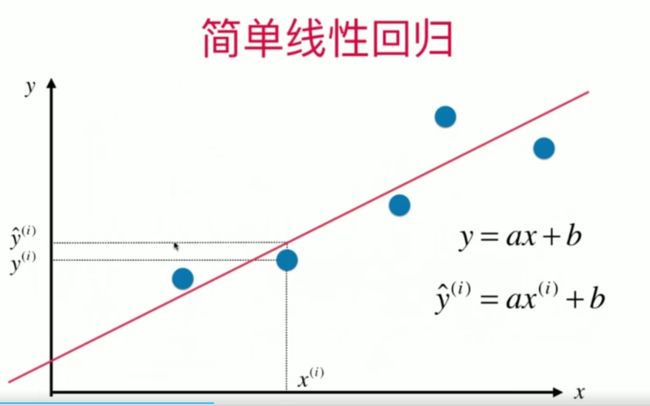
在简单线性回归中,输入x只有一个特征,通过调整a和b的参数值,来拟合从x到y的线性关系。下图为进行拟合所需要优化的目标,也即是MES(Mean Squared Error),只不过省略了平均的部分(除以m)。
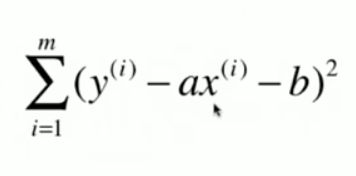
对于简单线性回归,只有两个参数a和b,通过对MSE优化目标求导后取极值点极值(最小二乘法),即可求得最优a和b如下,所以在训练简单线性回归模型时,也只需要根据数据求解这两个参数值即可。

下面使用波士顿房价数据集中,索引为5(第6个特征)的特征RM (average number of rooms per dwelling:每个住宅的平均房间数)来进行简单线性回归。其中使用的评价指标为:



以及R方指标。这里R方指标一般情况下可以将对模型的评价压缩到[0,1]之间(也可能是负数),值越接近1效果越好。在式子分子分母中的两项都可以认作在算均方误差,只不过分子使用我们训练的线性回归模型的输出,分母则使用真实标签数据的平均值来做均方误差,表示对每个样本,都是一个固定值瞎猜结果,其值等价于实际标签值的方差。通过模型的均方误差和瞎猜产生的误差做对比,就可以将评价指标限定在[0,1](如果模型比瞎猜还差就会成为负数)。


# 以sklearn的形式对simple linear regression 算法进行封装
import numpy as np
import sklearn.datasets as datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error,mean_absolute_error
np.random.seed(123)
class SimpleLinearRegression():
def __init__(self):
"""
initialize model parameters
"""
self.a_=None
self.b_=None
def fit(self,x_train,y_train):
"""
training model parameters
Parameters
----------
x_train:train x ,shape:data [N,]
y_train:train y ,shape:data [N,]
"""
assert (x_train.ndim==1 and y_train.ndim==1),\
"""Simple Linear Regression model can only solve single feature training data"""
assert len(x_train)==len(y_train),\
"""the size of x_train must be equal to y_train"""
x_mean=np.mean(x_train)
y_mean=np.mean(y_train)
self.a_=np.vdot((x_train-x_mean),(y_train-y_mean))/np.vdot((x_train-x_mean),(x_train-x_mean))
self.b_=y_mean-self.a_*x_mean
def predict(self,input_x):
"""
make predictions based on a batch of data
Parameters
----------
input_x:shape->[N,]
"""
assert input_x.ndim==1 ,\
"""Simple Linear Regression model can only solve single feature data"""
return np.array([self.pred_(x) for x in input_x])
def pred_(self,x):
"""
give a prediction based on single input x
"""
return self.a_*x+self.b_
def __repr__(self):
return "SimpleLinearRegressionModel"
if __name__ == '__main__':
boston_data = datasets.load_boston()
print(boston_data['DESCR'])
x = boston_data['data'][:, 5] # total x data (506,)
y = boston_data['target'] # total y data (506,)
# keep data with target value less than 50.
x = x[y < 50] # total x data (490,)
y = y[y < 50] # total x data (490,)
plt.scatter(x, y)
plt.show()
# train size:(343,) test size:(147,)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
regs = SimpleLinearRegression()
regs.fit(x_train, y_train)
y_hat = regs.predict(x_test)
rmse = np.sqrt(np.sum((y_hat - y_test) ** 2) / len(x_test))
mse = mean_squared_error(y_test, y_hat)
mae = mean_absolute_error(y_test, y_hat)
# notice
R_squared_Error = 1 - mse / np.var(y_test)
print('mean squared error:%.2f' % (mse))
print('root mean squared error:%.2f' % (rmse))
print('mean absolute error:%.2f' % (mae))
print('R squared Error:%.2f' % (R_squared_Error))
a = regs.a_
b = regs.b_
x_plot = np.linspace(4, 8, 50)
y_plot = x_plot * a + b
plt.scatter(x, y)
plt.plot(x_plot, y_plot, color='red')
plt.show()
输出结果:
mean squared error:26.74
root mean squared error:5.17
mean absolute error:3.85
R squared Error:0.50
数据的可视化:

1.2 多元线性回归的正规方程解
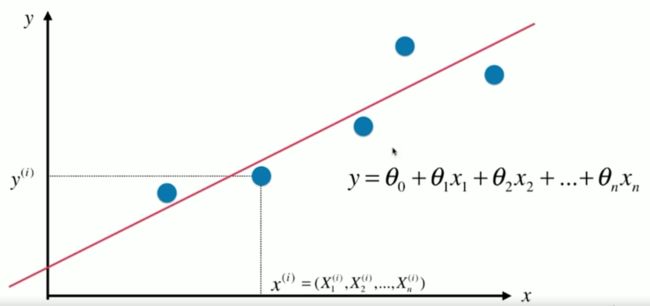
多元线性回归中,单个x的样本拥有了多个特征,也就是上图中带下标的x。
其结构可以用向量乘法表示出来:
为了便于计算,一般会将x增加一个为1的特征,方便与截距bias计算。
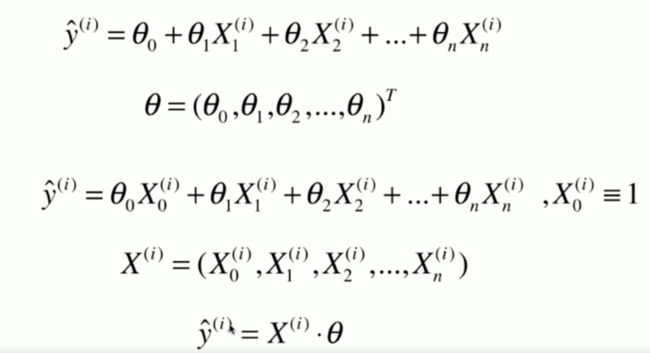
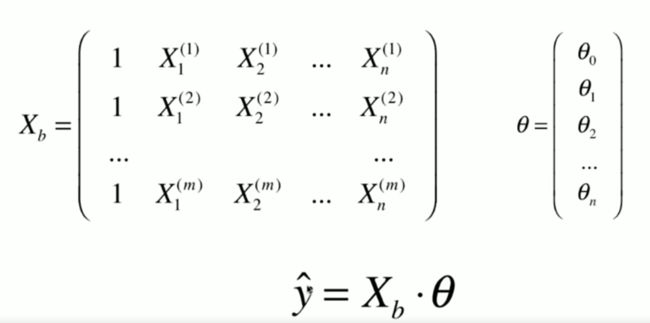
而多元线性回归的优化目标与简单线性回归一致。
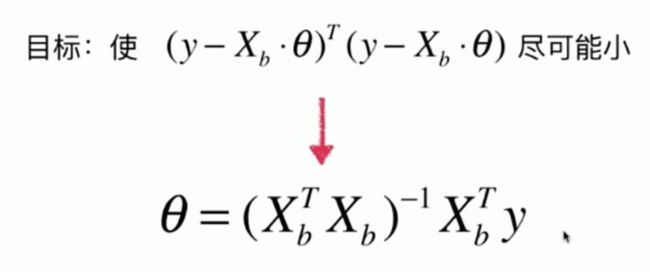
通过矩阵求导计算,可以得到方程解,但求解的时间复杂度很高。

下面使用正规方程解的形式,来对波士顿房价的所有特征做多元线性回归。
from math import sqrt
import numpy as np
#from PlayML.metrics import r2_score
from sklearn.model_selection import train_test_split
import sklearn.datasets as datasets
#from PlayML.metrics import root_mean_squared_error
np.random.seed(123)
def mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的MSE"""
assert len(y_true) == len(y_predict), \
"the size of y_true must be equal to the size of y_predict"
return np.sum((y_true - y_predict)**2) / len(y_true)
def r2_score(y_true, y_predict):
"""计算y_true和y_predict之间的R Square"""
return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)
def root_mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的RMSE"""
return sqrt(mean_squared_error(y_true, y_predict))
class LinearRegression():
def __init__(self):
self.coef_=None # coeffient
self.intercept_=None # interception
self.theta_=None
def fit_normal(self, x_train, y_train):
"""
use normal equation solution for multiple linear regresion as model parameters
Parameters
----------
theta=(X^T * X)^-1 * X^T * y
"""
assert x_train.shape[0] == y_train.shape[0],\
"""size of the x_train must be equal to y_train """
X_b=np.hstack([np.ones((len(x_train), 1)), x_train])
self.theta_=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train) # (featere,1)
self.coef_=self.theta_[1:]
self.intercept_=self.theta_[0]
def predict(self,x_pred):
"""给定待预测数据集X_predict,返回表示X_predict的结果向量"""
assert self.intercept_ is not None and self.coef_ is not None, \
"must fit before predict!"
assert x_pred.shape[1] == len(self.coef_), \
"the feature number of X_predict must be equal to X_train"
X_b=np.hstack([np.ones((len(x_pred),1)),x_pred])
return X_b.dot(self.theta_)
def score(self,x_test,y_test):
"""
Calculate evaluating indicator socre
Parameters
---------
x_test:x test data
y_test:true label y for x test data
"""
y_pred=self.predict(x_test)
return r2_score(y_test,y_pred)
def __repr__(self):
return "LinearRegression"
if __name__ == '__main__':
# use boston house price dataset for test
boston_data = datasets.load_boston()
x = boston_data['data'] # total x data (506,)
y = boston_data['target'] # total y data (506,)
# keep data with target value less than 50.
x = x[y < 50] # total x data (490,)
y = y[y < 50] # total x data (490,)
# train size:(343,) test size:(147,)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3,random_state=123)
regs = LinearRegression()
regs.fit_normal(x_train, y_train)
# calc error
score=regs.score(x_test,y_test)
rmse=root_mean_squared_error(y_test,regs.predict(x_test))
print('R squared error:%.2f' % (score))
print('Root mean squared error:%.2f' % (rmse))
输出结果:
R squared error:0.79
Root mean squared error:3.36
1.3 使用梯度下降求解多元线性回归
使用梯度下降的方法,在数据比较多的情况下会比方程解快很多。代码也不难,只是关于参数梯度的向量化推导有一点复杂,还有就是训练前要先进行数据标准化。
损失函数与之前相同,还是使用MSE损失。

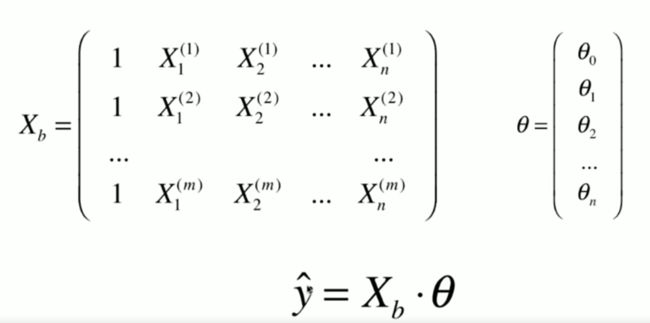


为了让梯度为列向量,再做依次转置,得到最终的结果。
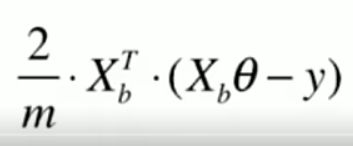
import numpy as np
from math import sqrt
import sklearn.datasets as datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def accuracy_score(y_true, y_predict):
"""计算y_true和y_predict之间的准确率"""
assert len(y_true) == len(y_predict), \
"the size of y_true must be equal to the size of y_predict"
return np.sum(y_true == y_predict) / len(y_true)
def mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的MSE"""
assert len(y_true) == len(y_predict), \
"the size of y_true must be equal to the size of y_predict"
return np.sum((y_true - y_predict)**2) / len(y_true)
def root_mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的RMSE"""
return sqrt(mean_squared_error(y_true, y_predict))
def mean_absolute_error(y_true, y_predict):
"""计算y_true和y_predict之间的MAE"""
assert len(y_true) == len(y_predict), \
"the size of y_true must be equal to the size of y_predict"
return np.sum(np.absolute(y_true - y_predict)) / len(y_true)
def r2_score(y_true, y_predict):
"""计算y_true和y_predict之间的R Square"""
return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)
class LinearRegression:
def __init__(self):
"""初始化Linear Regression模型"""
self.coef_ = None
self.intercept_ = None
self._theta = None
def fit_normal(self, X_train, y_train):
"""根据训练数据集X_train, y_train训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self, X_predict):
"""给定待预测数据集X_predict,返回表示X_predict的结果向量"""
assert self.intercept_ is not None and self.coef_ is not None, \
"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_), \
"the feature number of X_predict must be equal to X_train"
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
"""根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "LinearRegression()"
if __name__ == '__main__':
# use boston house price dataset
boston_data = datasets.load_boston()
x = boston_data['data'] # total x size (506,)
y = boston_data['target'] # total y size (506,)
# keep data with target value less than 50.
x = x[y < 50] # total x size (490,)
y = y[y < 50] # total x size (490,)
# notice! need data normalize
scaler=StandardScaler().fit(x)
x=scaler.transform(x)
# train size:(343,) test size:(147,)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=123)
regs = LinearRegression()
regs.fit_gd(x_train, y_train)
# calc error
score = regs.score(x_test, y_test)
rmse = root_mean_squared_error(y_test, regs.predict(x_test))
print('R squared error:%.2f' % (score))
print('Root mean squared error:%.2f' % (rmse))
print('coeffient:', regs.coef_.shape)
print('interception:', regs.intercept_.shape)
1.4 sklearn中的线性回归模型
import sklearn.datasets as datasets
from sklearn.linear_model import LinearRegression
import numpy as np
from sklearn.model_selection import train_test_split
from math import sqrt
np.random.seed(123)
def mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的MSE"""
assert len(y_true) == len(y_predict), \
"the size of y_true must be equal to the size of y_predict"
return np.sum((y_true - y_predict)**2) / len(y_true)
def root_mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的RMSE"""
return sqrt(mean_squared_error(y_true, y_predict))
if __name__ == '__main__':
# use boston house price dataset
boston_data = datasets.load_boston()
x = boston_data['data'] # total x size (506,)
y = boston_data['target'] # total y size (506,)
# keep data with target value less than 50.
x = x[y < 50] # total x size (490,)
y = y[y < 50] # total x size (490,)
# train size:(343,) test size:(147,)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=123)
regs = LinearRegression()
regs.fit(x_train, y_train)
# calc error
score = regs.score(x_test, y_test)
rmse = root_mean_squared_error(y_test, regs.predict(x_test))
print('R squared error:%.2f' % (score))
print('Root mean squared error:%.2f' % (rmse))
print('coeffient:',regs.coef_.shape)
print('interception:',regs.intercept_.shape)
R squared error:0.79
Root mean squared error:3.36
coeffient: (13,)
interception: ()