【AI理论学习】深入理解扩散模型：Diffusion Models（DDPM）（理论篇）

本文综合最近阅读的关于扩散模型的一些基础博客和文章整理而成。主要参考的内容来自 Calvin Luo 的论文，针对的对象主要是对扩散模型已经有一些基础了解的读者。

引言

继OpenAI在2021提出的文本转图像模型DALLE之后，越来越多的大公司卷入这个方向，例如谷歌相继推出了Imagen和Parti。一些主流的文本转图像模型，例如DALL·E 2，stable-diffusion和Imagen采用了扩散模型（Diffusion Model）作为图像生成模型，这也引发了对扩散模型的研究热潮。

与GAN相比，扩散模型训练更稳定，而且能够生成更多样的样本，OpenAI的论文Diffusion Models Beat GANs on Image Synthesis也证明了（不采用这个不等式的推导见博客What are Diffusion Models?），对于网络训练来说，其训练目标为VLB取负：

进一步对训练目标进行分解可得：

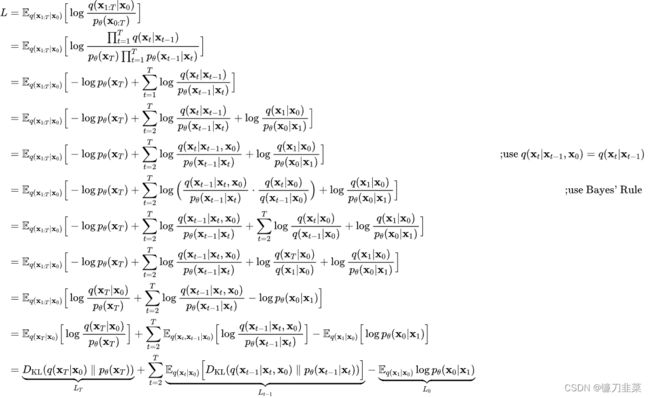
可以看到最终的优化目标共包含$T+1$项，其中$L_0$可以看成是原始数据重建，优化的是负对数似然，$L_0$可以用估计的$\mathcal{N}({\mathrm{x}}_0;{\mu }_{\theta }({\mathrm{x}}_1,1),{\sum }_{\theta }({\mathrm{x}}_1,1)$来构建一个离散化的decoder来计算（见DDPM论文3.3部分）；
而$L_T$计算的是最后得到的噪音的分布和先验分布的KL散度，这个KL散度没有训练参数，近似为0，因为先验$p({\mathrm{x}}_T)=\mathcal{N}(0,\mathtt{I})$，而扩散过程最后得到的随机噪音$p({\mathrm{x}}_T|{\mathrm{x}}_0)$也近似为$\mathcal{N}(0,\mathtt{I})$；
而$L_{t-1}$则是计算的是估计分布$p_{\theta }({\mathrm{x}}_{t-1}|{\mathrm{x}}_t)$和真实后验分布$q({\mathrm{x}}_{t-1}|{\mathrm{x}}_t,{\mathrm{x}}_0)$的KL散度，这里希望我们估计的去噪过程和依赖真实数据的去噪过程近似一致：

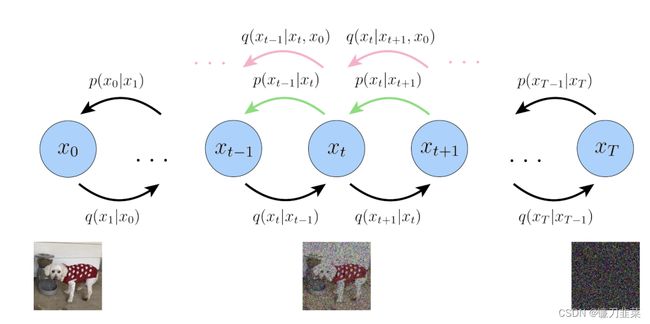
之所以在前面将$p_{\theta }({\mathrm{x}}_{t-1}|{\mathrm{x}}_t)$定义为一个用网络参数化的高斯分布$\mathcal{N}({\mathrm{x}}_{t-1};{\mu }_{\theta }({\mathrm{x}}_t,t),{\sum }_{\theta }({\mathrm{x}}_t,t))$，是因为要匹配的后验分布$q({\mathrm{x}}_{t-1}|{\mathrm{x}}_t,{\mathrm{x}}_0)$也是一个高斯分布。对于训练目标$L_0$和$L_{t-1}$来说，都是希望得到训练好的网络${\mu }_{\theta }({\mathrm{x}}_t,t)$和${\sum }_{\theta }({\mathrm{x}}_t,t)$（对于$L_0$，$t=1$）。
DDPM对$p_{\theta }({\mathrm{x}}_{t-1}|{\mathrm{x}}_t)$做了进一步简化，采用固定的方差：${\sum }_{\theta }({\mathrm{x}}_t,t)={\sigma }_t^2\mathtt{I}$，这里的${\sigma }_t^2$可以设定为${\beta }_t$或者${\tilde{\beta }}_t$（这其实是两个极端，分别是上限和下限，也可以采用可训练的方差，见论文Improved Denoising Diffusion Probabilistic Models和Analytic-DPM: an Analytic Estimate of the Optimal Reverse Variance in Diffusion Probabilistic Models）。


这里假定${\sigma }_t^2={\tilde{\beta }}_t$，那么：
$$q({\mathrm{x}}_{t-1}|{\mathrm{x}}_t,{\mathrm{x}}_0)=\mathcal{N}({\mathrm{x}}_{t-1};\tilde{\mu }({\mathrm{x}}_t,{\mathrm{x}}_0),{\sigma }_t^2\mathtt{I})p_{\theta }({\mathrm{x}}_{t-1}|{\mathrm{x}}_t)=\mathcal{N}({\mathrm{x}}_{t-1};{\mu }_{\theta }({\mathrm{x}}_t,t),{\sigma }_t^2\mathtt{I})$$
对于两个高斯分布的KL散度，其计算公式为：

那么就有：

那么优化目标$L_{t-1}$即为：$$L_{t-1}={\mathbb{E}}_{q({\mathrm{x}}_t|{\mathrm{x}}_0)}[\frac{1}{2{\sigma }_t^2}||{\tilde{\mu }}_t({\mathrm{x}}_t,{\mathrm{x}}_0)-{\mu }_{\theta }({\mathrm{x}}_t,t)|{|}^2]$$
从上述公式来看，我们希望网络学习到的均值${\mu }_{\theta }({\mathrm{x}}_t,t)$和后验分布的均值${\tilde{\mu }}_t({\mathrm{x}}_t,{\mathrm{x}}_0)$一致。不过DDPM发现预测均值并不是最好的选择。根据前面得到的扩散过程的特性，有：$${\mathrm{x}}_t({\mathrm{x}}_0,ϵ)=\sqrt{{\bar{\alpha }}_t}{\mathrm{x}}_0+\sqrt{1-{\bar{\alpha }}_tϵ}\text{ where }ϵ\sim \mathcal{N}(0,\mathtt{I})$$
将这个公式带入上述优化目标，可以得到：

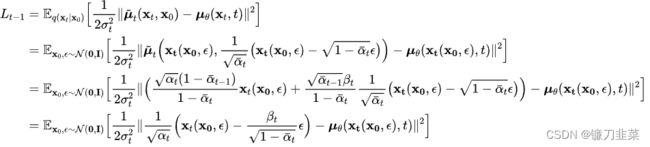
进一步地，对${\mu }_{\theta }({\mathrm{x}}_t({\mathrm{x}}_0,ϵ),t)$也进行重参数化，变成：$${\mu }_{\theta }({\mathrm{x}}_t({\mathrm{x}}_0,ϵ),t)=\frac{1}{{\sqrt{\alpha }}_t}({\mathrm{x}}_t({\mathrm{x}}_0,ϵ)-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }({\mathrm{x}}_t({\mathrm{x}}_0,ϵ),t))$$
这里的${ϵ}_{\theta }$是一个基于神经网络的拟合函数，这意味着由原来的预测均值而换成预测噪音$ϵ$。我们将上述等式代入优化目标，可以得到：

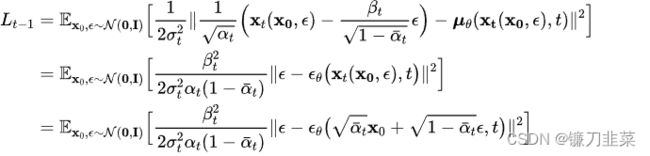
DDPM进一步对上述目标进行了简化，即去掉了权重参数，变成了$L_{t-1}^{simple}={\mathbb{E}}_{{\mathrm{x}}_0,ϵ\sim \mathcal{N}(0,\mathtt{I})}[||ϵ-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathrm{x}}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ,t)|{|}^2]$。这里的$t$在$[1,T]$范围内取值（如前所述，其中取1时对应$L_0$）。由于去掉了不同$t$的权重系数，所以这个简化的目标其实是VLB优化目标进行了reweight。从DDPM的对比实验结果来看，预测噪音比预测均值效果要好，采用简化版本的优化目标比VLB目标效果要好：

虽然扩散模型背后的推导比较复杂，但是最终得到的优化目标非常简单，就是让网络预测的噪音和真实的噪音一致。DDPM的训练过程也非常简单，如下图所示：随机选择一个训练样本->从1-T随机抽样一个t->随机产生噪音-计算当前所产生的带噪音数据（红色框所示）->输入网络预测噪音->计算产生的噪音和预测的噪音的L2损失->计算梯度并更新网络。

一旦训练完成，其采样过程也非常简单，如上所示：我们从一个随机噪音开始，并用训练好的网络预测噪音，然后计算条件分布的均值（红色框部分），然后用均值加标准差乘以一个随机噪音，直至t=0完成新样本的生成（最后一步不加噪音）。

不过实际的代码实现和上述过程略有区别（见https://github.com/hojonathanho/diffusion/issues/5：先基于预测的噪音生成${\mathrm{x}}_0$，并进行了clip处理（范围[-1, 1]，原始数据归一化到这个范围），然后再计算均值。这应该算是一种约束，既然模型预测的是噪音，那么我们也希望用预测噪音重构处理的原始数据也应该满足范围要求。

模型设计

前面我们介绍了扩散模型的原理以及优化目标，那么扩散模型的核心就在于训练噪音预测模型，由于噪音和原始数据是同维度的，所以我们可以选择采用AutoEncoder架构来作为噪音预测模型。DDPM所采用的模型是一个基于residual block和attention block的U-Net模型。如下所示：

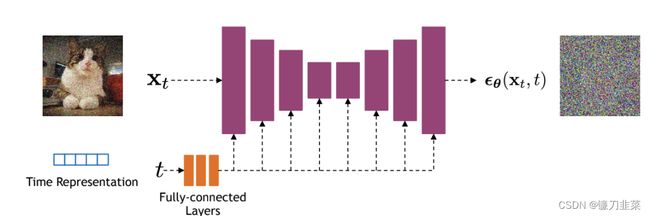
U-Net属于encoder-decoder架构，其中encoder分成不同的stages，每个stage都包含下采样模块来降低特征的空间大小（H和W），然后decoder和encoder相反，是将encoder压缩的特征逐渐恢复。U-Net在decoder模块中还引入了skip connection，即concat了encoder中间得到的同维度特征，这有利于网络优化。DDPM所采用的U-Net每个stage包含2个residual block，而且部分stage还加入了self-attention模块增加网络的全局建模能力。

另外，扩散模型其实需要的是个噪音预测模型，实际处理时，我们可以增加一个time embedding（类似transformer中的position embedding）来将timestep编码到网络中，从而只需要训练一个共享的U-Net模型。具体地，DDPM在各个residual block都引入了time embedding，如上图所示。

代码实现

最后，我们基于PyTorch框架给出DDPM的具体实现，这里主要参考了三套代码实现：

• GitHub - hojonathanho/diffusion: Denoising Diffusion Probabilistic Models（官方TensorFlow实现）
• GitHub - openai/improved-diffusion: Release for Improved Denoising Diffusion Probabilistic Models （OpenAI基于PyTorch实现的DDPM+）
• GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch

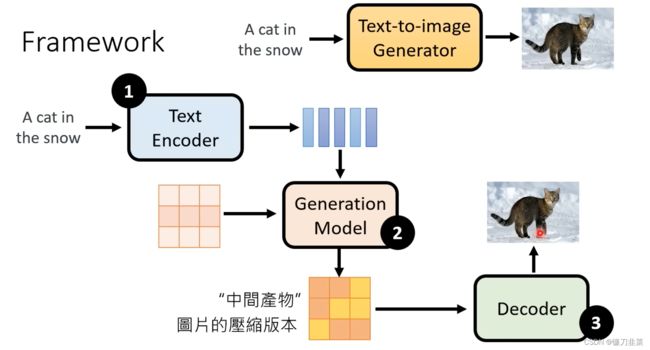
Stable Diffusion、DALL-E、Imagen背后共同的套路

Framework

Component组件：

1. Text Encoder: 使用Text Encoder将文本生成一个embedding，
2. Generation Model：然后和噪声一起生成一个Generation Model，得到一个中间产物
3. Decoder： 使用Decoder都得到带有噪声图片

Stable Diffusion

High-Resolution Image Synthesis with Latent Diffusion Models
https://arxiv.org/abs/2112.10752

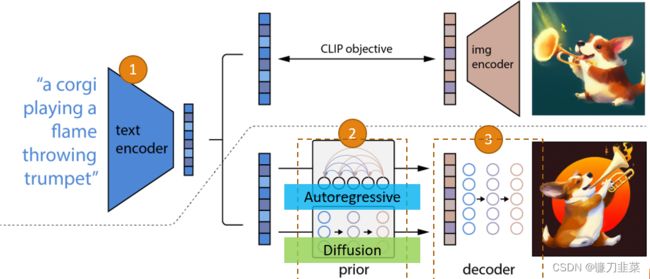
DALL-E series

Imagen

Text encoder

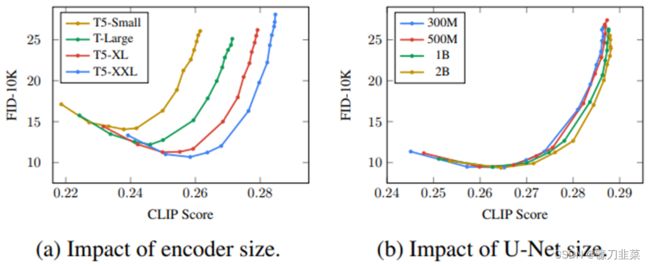
Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding
https://arxiv.org/abs/2205.11487

Decoder

Decoder can be trained without labelled data.

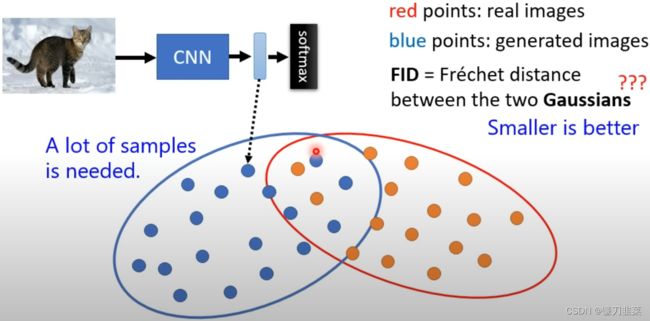
什么是FID（Frechet Inception Distance）

什么是CLIP（Contrastive Language-Image Pre-Training）

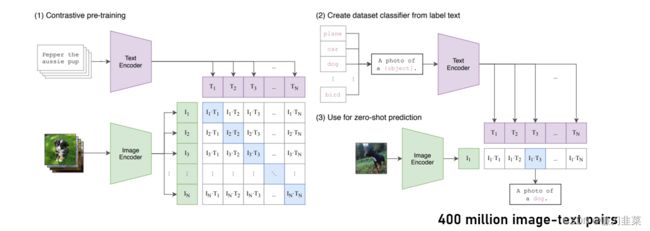
Learning Transferable Visual Models From Natural Language Supervision
https://arxiv.org/abs/2103.00020

Diffusion Model: Summary

Diffusion Model in PyTorch

The easier way to use a Diffusion Model in PyTorch is to use the denoising-diffusion-pytorch package.

pip install denoising_diffusion_pytorch

一个示例代码：

import torch
from denoising_diffusion_pytorch import Unet, GaussianDiffusion
model = Unet(
    dim = 64,
    dim_mults = (1, 2, 4, 8)
)
model = Unet(
    dim = 64,
    dim_mults = (1, 2, 4, 8)
)
diffusion = GaussianDiffusion(
    model,
    image_size = 128,
    timesteps = 1000,   # number of steps
    loss_type = 'l1'    # L1 or L2
)
training_images = torch.randn(8, 3, 128, 128)
loss = diffusion(training_images)
loss.backward()
sampled_images = diffusion.sample(batch_size = 4)

参考资料

1. 从大一统视角理解扩散模型（Diffusion Models）
2. What are Diffusion Models?
3. Understanding Diffusion Models: A Unified Perspective
4. Generative Modeling by Estimating Gradients of the Data Distribution
5. Stable Diffusion、DALL-E、Imagen 背後共同的套路
6. 带你深入理解扩散模型DDPM
7. https://colab.research.google.com/github/huggingface/notebooks/blob/main/diffusers/stable_diffusion.ipynb#scrollTo=AAVZStIokTVv