MPC模型预测控制简单实现（Matlab代码实现）

       目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

模型预测控制是一种基于模型的闭环优化控制策略。

预测控制算法的三要素：内部（预测）模型、参考轨迹、控制算法。现在一般则更清楚地表述为内部（预测）模型、滚动优化、反馈控制。 

大量的预测控制权威性文献都无一例外地指出, 预测控制最大的吸引力在于它具有显式处理约束的能力, 这种能力来自其基于模型对系统未来动态行为的预测, 通过把约束加到未来的输入、输出或状态变量上, 可以把约束显式表示在一个在线求解的二次规划或非线性规划问题中. 

模型预测控制具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和并联性，并能方便的处理过程被控变量和操纵变量中的各种约束。

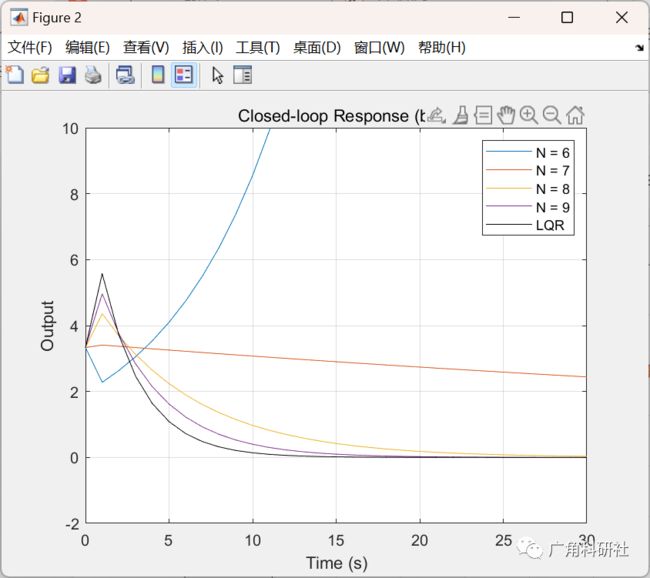
2 运行结果

主函数部分代码：

% MPC Ex1 |clc;close all;clear all;​A = [ 4/3 -2/3; 1 0 ];B = [ 1; 0 ];C = [ -2/3 1 ];D = 0;​​Q = C'*C + 0.001*eye(2);R =  0.001;Pf = Q;​x0 = [10;10];​dt = 1;t = 0:dt:30;u = zeros(size(t));​​sys = ss(A,B,C,D,dt);​%{sysc = d2c(sys);​figure;impulse(sys);grid on;figure;step(sys,sysc);grid on;​figure;lsim(sys,u,t,x0);grid on;%}​%% Ex1​​%% Ex2​N = 6;dN = 1;for i = 1:4    [K0,S0] = finite_dlqr(A,B,Q,R,Pf,N);    sys_cl = ss(A+B*K0,B,C,D,dt);    [y(:,i) t x(:,:,i)] = lsim(sys_cl,u,t,x0);    M{i} = A'*S0*A - S0;    legendinfo{i} = ['N = ' num2str(N)];    N = N + dN;end​figure;for i = 1:4    plot(x(:,1,i),x(:,2,i),'-o');    axis([-20 20 -20 20]);    hold on;endhold off;xlabel('x_1');ylabel('x_2');grid on;legend(legendinfo);title('Closed-loop Response (a)');​figure;plot(t,y(:,1:end));ylim([-2 10]);hold on;​​​​%% Ex3​[K,S] = dlqr(A,B,Q,R);sys_cl = ss(A-B*K,B,C,D,dt);​[y t] = lsim(sys_cl,u,t,x0);plot(t,y,'k');legendinfo{i+1} = 'LQR';legend(legendinfo);grid on;title('Closed-loop Response (b)');xlabel('Time (s)');ylabel('Output');​​format longcost_infinite = x0'*S*x0;[K0,S0] = finite_dlqr(A,B,Q,R,Pf,8);cost_finite = x0'*S0*x0;[cost_infinite cost_finite cost_infinite-cost_finite] % test = lqr(sysd,Q,R)A'*S0*A - S0;A'*S*A - S;​

3 参考文献

I. S. Mohamed, S. Rovetta, T. D. Do, T. Dragicević and A. A. Z. Diab, "A Neural-Network-Based Model Predictive Control of Three-Phase Inverter With an Output LC Filter," in IEEE Access, vol. 7, pp. 124737-124749, 2019.

部分理论引用网络文献，若有侵权联系博主删除。