【多目标进化优化】Pareto 定义及基于 Pareto 的多目标进化算法的算法流程

声明

本文内容来源于 《多目标进化优化》 郑金华 邹娟著，非常感谢两位老师的知识分享，如有侵权，本人立即删除，同时在此表示，本文内容仅学习使用，禁止侵权，谢谢！

0 前言

• 多目标优化在推荐系统、物流配送、路径规划等中有广泛的应用

• 一些多目标优化算法主要就是求解问题的 Pareto 前沿或者近似前沿。从目标空间来看，就是他的边界了。

• 在多目标优化中，对于不同的子目标函数可能有不同的优化目标，有的可能是最大化目标函数，也有的可能是最小化目标函数，归纳起来，不外乎下列三种可能的情况:

  • ① 最小化所有的子目标函数。
  • ② 最大化所有的子目标函数。
  • ③ 最小化部分子目标函数,而最大化其他子目标函数。

• 如 ③ 中任何不同表达形式的多目标优化问题都可以转换成统一的表示形式：① 或 ②

1. 优化问题

1.1 无约束的单目标优化问题

$$mi{n}_{x}f(x),x\in R^N\text{\hspace{1em}(1)}$$
其中，x 的取值为 n 维实数空间 R^N, f(x) 为连续一阶可导函数

1.2 无约束的多目标优化问题

$$mi{n}_{x}F(x)=[f_1(x),f_2(x),...,f_K(x)],x\in R^N\text{\hspace{1em}(2)}$$
其中，K 为子目标的个数，$x$ 的取值为 N 维实数空间，$f_k(x)$ 为连续一阶可导函的子目标函数。

1.3 带约束的单目标优化问题

$$mi{n}_{x}f(x)$$
$$s.t.g_i(x)\ge 0,i\in [1,M]\text{\hspace{1em}(3)}$$
$$h_j(x)=0,j\in [1,L]$$

其中 $s.t.$ 为 subject to 的缩写，表示受限于的意思

令 $D$ 为上述多目标优化问题的可行域，即：
$$D=\{x|g_i(x)\ge 0,i\in [1,M],h_j(x)=0,j\in [1,L]\}$$

1.4 带约束的多目标优化问题

带约束的多目标问题 MOP (multi-objective optimization problem)
$$mi{n}_{x}F(x)=[f_1(x),f_2(x),...,f_K(x)]$$
$$s.t.g_i(x)\ge 0,i\in [1,M]\text{\hspace{1em}(4)}$$
$$h_j(x)=0,j\in [1,L]$$
令 $D$ 为上述多目标优化问题的可行域，即
$$D=\{x|g_i(x)\ge 0,i\in [1,M],h_j(x)=0,j\in [1,L]\}$$

2. 多目标个体进化之间的关系

我们对两个量之间的大小关系进行比较时，在单目标情况下，如常量 5 和 8，显然有 5 比 8 小或 8 比 5 大，对两个变量（个体）x 和 y 进行比较时，可能存在三种关系：x 大于 y、x 等于 y、x 小于 y。在多目标情况下，由于每个个体有多个属性，比较两个个体之间的关系不能使用简单的大小关系。如两个目标的个体（2，6）和（3，5)，在第一个目标上有 2 小于 3，而在第二个目标上又有 6 大于 5，这种情况下个体（2，6）和（3，5）之间的关系是什么呢?另一种情况，如个体（2，6）和（3，8)，它们之间的关系又是什么呢?当目标数大于 2 时,又如何比较不同个体之间的关系呢? 为此，这里讨论多目标个体之间非常重要的一种关系，叫做支配关系。

定义 2.1 可行解

对于某个 $x\in X$，如果 x 满足（4）中的约束条件 $g_i(x)\ge 0,i\in [1,M]和h_j(x)=0,j\in [1,L]$ 则称 $x$ 为可行解

定义 2.2 可行解集合

由 $X$ 中的所有的可行解组成的集合称为可行解集合，记为 $X_f$，且 $X_f\subseteq X$，通常用 $\Omega$ 表示可行解结合

定义 2.3 (个体之间的支配关系)

设 p 和 q 是进化群体 Pop 中的任意两个不同的个体，我们称 p 支配（dominate) q，则必须满足下列两个条件:

• ① 对所有的子目标，p不 比 q 差，即 $f_k(p)\le f_k(q)(k=l,2,\dots ,r)$
• ② 至少存在一个子目标，使 p 比 q 好。即$\exists l\in \{1,2,\dots ,r\},使f_l(p)<f_l(q)$。其中，r为子目标的数量。

此时称 p 为非支配的（non-dominated)，或非劣的或占优的，q 为被支配的（dominated)。表示为 p $\succ$ q，其中 ‘$\succ$’ 是支配关系(dominate relation)。

值得说明的是，这里所定义的支配关系是“小”个体支配“大”个体，也可以按照完全相反的方式来定义支配关系，这取决于所求解的问题。此外，本文在表述上将 “ p 支配 q”表示为 “p $\succ$ q”，而在有些文献上则刚好相反，将“ p 支配 q”表示为 “p $\succ$ q”。

定义2.1 所定义的支配关系是针对决策空间的，类似地，可以在目标空间中定义支配关系，如定义2.2所示

定义 2.3 (目标空间中的支配关系)

设 $U=(u_1,u_2,\dots ,u_r,)$ 和 $V=(v_1,v2,\dots ,v_r,)$ 是目标空间中的两个向量，称 $U$ 支配 $V$（表示为 $U\succ V$)，当且仅当 $u_k\le v_k(k=l,2，\dots ，r)$，且 $\exists l\in \{1,2,\dots ,r\}$，使 $u_1<v_1$

据定义 2.2 可以得出结论：(2，6）支配（3，8)，(2，6）和（3，5）之间互相不支配。

值得说明的是，决策空间中的支配关系与目标空间中的支配关系是一致的，这一点由定义 2.1 可以看出，因为决策空间中的支配关系实质上是由目标空间中的支配关系决定的。此外，个体之间的支配关系还有程度上的差异，可参见定义 2.3 和定义 2.4

定义 2.4 (弱非支配，weak nondominance)

若不存在 $X\in \Omega$，使 $f_k(X)<f_k(X^{\ast })(k=l，2，\dots ，r)$成立，则称 $X^{\ast }\in \Omega$ 为弱非支配解（a weakly nondominated solution)

解释： 在求所有目标函数最小值时，在 $X$ 可行域中，即图中 S 区域, 不存在 $X^{\ast }$ 对应的所有目标函数值都大于可行域中某一点的所有对应函数值，则 $X^{\ast }$ 为弱非支配解，对应与图中的左侧弧线和底部直线标红部分

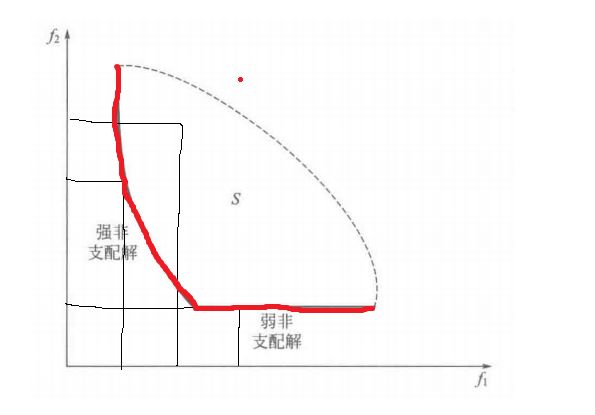
定义 2.5 (强非支配，strongnondominance)

若不存在 $X\in \Omega$，使 $f_k(X)\le f_k(X^{\ast })(k=l,2,\dots ,r)$ 成立，且至少存在一个 $i\in \{1，2，\dots ，r\}$，使 $f_i(X)<f_i(X^{\ast })$，则称 $X^{\ast }\in \Omega$ 为强非支配解（a strongly nondominated solution)

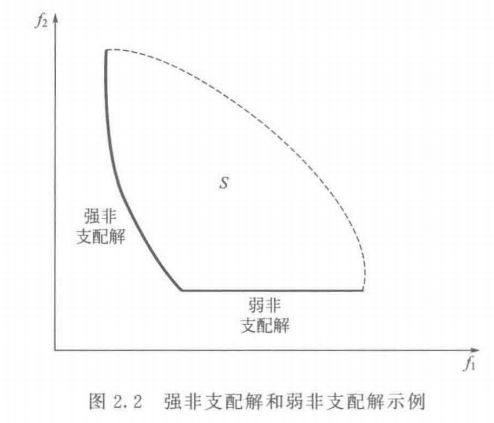
解释： 在求所有目标函数最小值时，在 $X$ 可行域中，即图中 S 区域, 不存在 $X^{\ast }$ 对应的所有目标函数值都大于等于可行域中某一点的所有对应函数值，并且存在某个子目标函数值，使得 $X^{\ast }$ 对应的目标函数值比某一点大（不仅仅是等于），则 $X^{\ast }$ 为强非支配解

由以上定义可以看出，如果 $X^{\ast }$ 是强非支配的,则 $X^{\ast }$ 也是弱非支配的，反之则不然。对于两个目标的情况,如上图所示,在目标空间中强非支配解均落在粗曲线上,弱非支配解则落在细的直线上。

2. 多目标优化的解集:解集定义

• 对于多目标优化问题 MOP，通常不存在解 $x^{\ast }\in D$,使得目标 $f_i(x),\forall i\in [1,K]$, 同时达到最小值

• 在描述 MOP 的解集之前，我们先来定义多目标里面的相等、严格小于、小于、小于且不相等的含义：

• 设 $R^N$ 为 $N$ 维实向量空间，$y=(y_1,y_2,...,y_N{)}^T,z=(z_1,z_2,...,z_N{)}^T$
  $$f(n)=\{\begin{array}{ll}相等& \text{y=z⇔yi=zi,i=1,2,...,N }\\ 严格小于& \text{y<z⇔yi=zi,i=1,2,...,N }\\ 小于& \text{y<z⇔yi=zi,i=1,2,...,N }\\ 小于且不相等& \text{y≤z⇔yi=zi,i=1,2,...,N,且y=z }\end{array}\text{\hspace{1em}(5)}$$

3. Pareto 最优解

多目标优化中的最优解通常称为 Pareto 最优解

定义 2.5 最优解

给定一个多目标优化问题 $f(X)$，它的最优解 $X^{\ast }$ 定义为

$$f(X^{\ast })=\underset{X\in \Omega }{optf(X)}$$
其中：
$$f:\Omega \to {\mathbb{R}}^r$$
式中，$\Omega$ 为可行解，即：
$$\Omega =\{x\in {\mathbb{R}}^n|g_i(x)\ge 0,i\in [1,M],h_j(x)=0,j\in [1,L]\}$$
称 $\Omega$ 为决策变量空间，向量函数 $f(X)$ 将 $\Omega \subseteq {\mathbb{R}}^n$ 映射到集合 $\Pi \subseteq {\mathbb{R}}^r$，$\Pi$ 是目标函数空间

定义 2.6 最优解

给定一个多目标优化问题 $minf(X)$，称 $X^{\ast }\in \Omega$ 是最优解，若 $\forall X\in \Omega$，满足下列条件:
$$\underset{i\in I}{\wedge }(f_i(X)\ge f_i(X^{\ast }))$$

定义 2.7 Pareto 最优解

给定一个多目标优化问题 $minf(X)$，若 $X^{\ast }\in \Omega$，且不存在其他的 $\overline{X^{\ast }}\in \Omega$ 使得 $f_j(X^{\ast })\ge f_j(\overline{X^{\ast }})(j=1,2,\dots ,r）$成立，且其中至少一个是严格不等式，则称 $X\ast$ 是 $minf(X)$ 的 Pareto 最优解。式中，$\Omega$ 是可行解集

定义 2.8 强/弱 Pareto 最优解

给定一个多目标优化问题 $minf(X)$，设 $X_1，X_2\in \Omega$，如果 $f(X_1)\le f(X_2)$，则称 $X_1$ 比 $X_2$ 优越；如果 $f(X_1)<f(X_2)$，则称 $X_1$ 比 $X_2$ 更优越

定义 $X^{\ast }\in \Omega$：若比 $X^{\ast }$ 更优越的 $X\in \Omega$ 不存在，则称 $X^{\ast }$ 为弱 Pareto 最优解；若 $X^{\ast }$ 比任何 $X\in \Omega$ 都优越，则称 $X^{\ast }$ 为完全 Pareto 最优解；若比 $X^{\ast }$ 优越的 $X\in \Omega$ 不存在，则称 $X^{\ast }$ 为强 Pareto 最优解。

定义 2.9 Pareto 最优解集

给定一个多目标优化问题 $minf(X)$, 它的最优解集定义为
$$P^{\ast }=\{X^{\ast }\}=\{X\in \Omega |\neg \exists X^{{}^{\prime }}\in \Omega ,f_j(X^{{}^{\prime }})\le f_j(\overline{X})(j=1,2,...,r)\}$$

多目标进化算法的优化过程是，针对每一代进化群体，寻找出其当前最优个体（即当前最优解)，称一个进化群体的当前最优解为非支配解（ non-dominated solution）或非劣解（non-inferior solution)；所有非支配解的集合称为当前进化群体的非支配集(non-dominated solution set，NDSet）或非劣解集，并使非支配集不断逼近真正的最优解集，最终达到最优，即使 $NDSe{t}^{\ast }\subseteq \{X^{\ast }\}$，$NDSe{t}^{\ast }$ 为算法运行结束时所求得的非支配集。

Pareto 最优边界

一个多目标优化问题的 Pareto 最优解集在其目标函数空间中的表现形式就是它的 Pareto 最优边界。Pareto 最优边界 $P{F}^{\ast }$ 或 $P{F}_{True}$( true Pareto front)定义如下:

给定一个多目标优化问题 $minf(X)$ 和它的最优解集 $\{X^{\ast }\}$, 它的 Pareto 最优边界定义为：
$$P{F}^{\ast }=\{f(X)=(f_1(X),f_2(X),...,f_m(x^{\ast }))|x^{\ast }\in \{X^{\ast }\}\}$$

请注意 Pareto 最优解集和 Pareto 最优边界之间的联系与区别。大家知道，多目标优化是从决策空间 $\Omega \subseteq {\mathbb{R}}^n$ 到目标空间 $\Pi \subseteq {\mathbb{R}}^r$ 的一个映射。Pareto 最优解集 $P^{\ast }$ 是决策向量空间的一个子集，即有 $P^{\ast }\subseteq \Omega \subseteq {\mathbb{R}}^n$；而 Pareto 最优边界则是目标向量空间的一个子集，即有 $P{F}^{\ast }\subseteq \Pi \subseteq {\mathbb{R}}^r$，说人话就是，最有解集是目标函数对应的 x 向量，Pareto 最优边界是目标函数的值组成的集合

一个多目标问题的最优解 $X^{\ast }\in P^{\ast }$ 或 $Y^{\ast }=minf(X^{\ast })\in P{F}^{\ast }$, 前者属于决策向量空间，后者属于目标向量空间

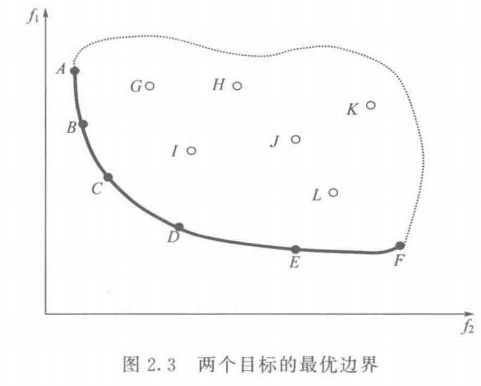
在目标空间中，最优解是目标函数的切点，它总是落在搜索区域的边界线（面）上。如上图所示，粗线段表示两个优化目标的最优边界。三个优化目标的最优边界构成一个曲面，三个以上的最优边界则构成超曲面。实心点A、B、C、D、E、F均处在最优边界上，它们都是最优解,是非支配的;空心点G、H、I、J、K、L落在搜索区域内,但不在最优边界上，不是最优解，是被支配的( dominated)，它们直接或间接受最优边界上的最优解支配。

利用 Pareto 最优解求解多目标优化问题

多目标遗传算法在优化过程中，初始时随机产生一个进化群体 $Po{p}_0$，然后按照某种策略构造 $Po{p}_0$ 的非支配集 $NDSe{t}_0$，此时的 $NDSe{t}_0$ 可能距离 $\{X^{\ast }\}$ 比较远。按照某种方法或策略产生一些个体，这些个体可以是被当前非支配集 $NDSe{t}_0$ 中个体所支配的，也可以是随机新产生的，连同 $NDSe{t}_0$ 中个体一起构成新的进化群体 $Po{p}_1$, 对新进化群体 $Po{p}_1$ 执行进化操作后，再构造新的非支配集 $NDSe{t}_1$。由于 $NDSe{t}_1$ 是在 $NDSe{t}_0$ 的基础上产生的，故 $NDSe{t}_1$ 比 $NDSe{t}_0$ 更接近 $\{X^{\ast }\}$。如此继续下去， 从理论上说，必能构造出 $$，使得当 $i\to \infty$ 时，为 Pareto 最优解集，即 $\underset{i\to \infty }{\lim }NDSe{t}_i=，$ 使 $NDSe{t}^{\ast }\subseteq \{X^{\ast }\}$。

4. 图文阐述 Pareto 最优解

两个目标函数

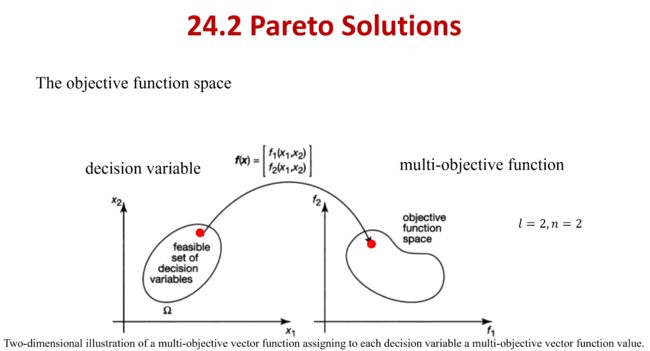
三个目标函数

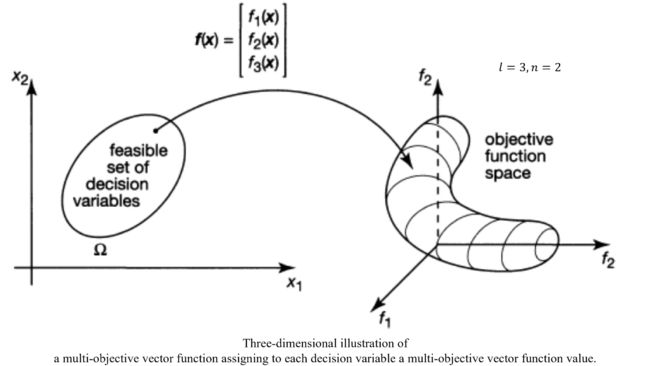
4.1 Pareto 支配 (Pareto Dominance)

定义：$\forall x_1,x_2\in X_f$，如果对于 $\forall i\in [1,M]$，都有 $f_i(x_1)\le f_i(x_2)$ 并且, $\exists j\in [1,L]$，使得 $f_j(x_1)<f_j(x_2)$ 则称 $x_1$ 支配 $x_2$，也称 $x_1$ 是 Pareto 占优的

4.1 Pareto 最优解

一个解 $x^{\ast }\in X_f$，若 $\neg \exists x\in X_f：x支配x^{\ast }$，则 $x^{\ast }$ 被称为 Pareto 最优解（或非支配解）

4.2 Pareto 最优解集

Pareto 最优解集是所有 Pareto 最优解的集合，定义如下：
$$P^{\ast }=\{x^{\ast }|\neg \exists x\in X_f：x支配x^{\ast }\}$$

4.3 Pareto 前沿面

Pareto 最优解集 $P^{\ast }$ 中的所有 Pareto 最优解对应的目标矢量组成的曲面称为 Pareto 前沿面 $P{F}^{\ast }$：
$$P{F}^{\ast }=\{F(x^{\ast })=(f_1(x^{\ast }),f_1(x^{\ast }),...,f_m(x^{\ast }){)}^T|x^{\ast }\in P^{\ast }\}$$

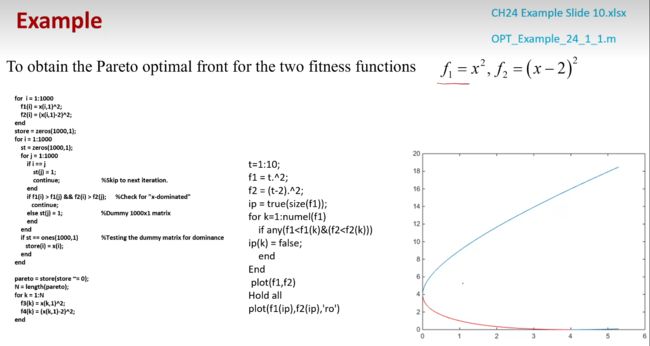
5. 实例阐述 Pareto

5.1 第一个实例

1：解 A 优于解 B（解 A 强帕累托支配解 B）

假设现在有两个目标函数，解 A 对应的目标函数值都比解 B 对应的目标函数值好，则称解A比解 B 优越，也可以叫做解 A 强帕累托支配解 B，举个例子

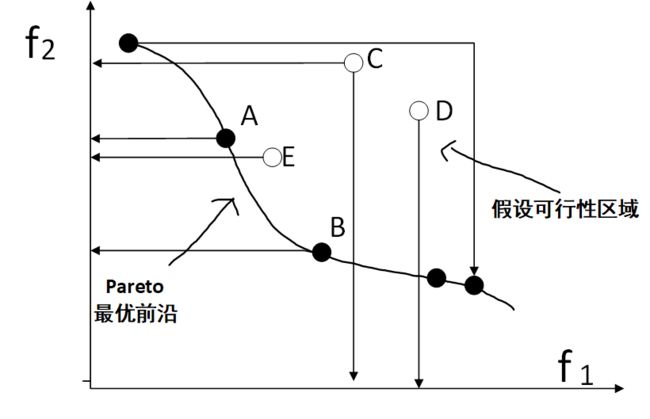
下图中代表的是两个目标的的解的情况，横纵坐标表示两个目标函数值，E 点表示的解所对应的两个目标函数值都小于 C，D 两个点表示的解所对应的两个目标函数值，所以解 E 优于解 C,D

2：解 A 无差别于解 B（解 A 能帕累托支配解 B）A,B两点严格意义上是非支配关系

同样假设两个目标函数，解 A 对应的一个目标函数值优于解 B 对应的一个目标函数值，但是解 A 对应的另一个目标函数值要差于解 B 对应的一个目标函数值，则称解 A 无差别于解B，也叫作解 A 能帕累托支配解 B，举个例子，还是上面的图，点 C 和点 D 就是这种情况，C 点在第一个目标函数的值比 D 小，在第二个函数的值比 D 大。

3：最优解

假设在设计空间中，解 A 对应的目标函数值优越其他任何解，则称解 A 为最优解，举个例子，下图的 $x_1$ 就是两个目标函数的最优解，使两个目标函数同时达到最小，但实际生活中这种解是不可能存在的，由此提出了帕累托最优解

4：帕累托最优解

同样假设两个目标函数，对于解 A 而言，在变量空间中找不到其他的解能够优于解A（这里的优于一定要两个目标函数值都优于 A 对应的函数值），那么解 A 就是帕累托最优解，举个例子，下图中应该找不到比 对应的目标函数都小的解了吧，即找不到一个解优于 $x_1$ 了，同理也找不到比 $x_2$ 更优的解了，所以这两个解都是帕累托最优解，实际上， 这个范围的解都是帕累托最优解。因此对于多目标优化问题而言，帕累托最优解只是问题的一个可接受解，一般都存在多个帕累托最优解，这个时候就需要自己决策了。

5：帕累托最优前沿

还是那张图 ，如下图所示，更好的理解一下帕累托最优解，实心点表示的解都是帕累托最优解，所有的帕累托最优解构成帕累托最优解集，这些解经目标函数映射构成了该问题的 Pareto 最优前沿或 Pareto 前沿面，即帕累托最优解对应的目标函数值就是帕累托最优前沿。

对于两个目标的问题，其 Pareto 最优前沿通常是条线。而对于多个目标，其 Pareto 最优前沿通常是一个超曲面。

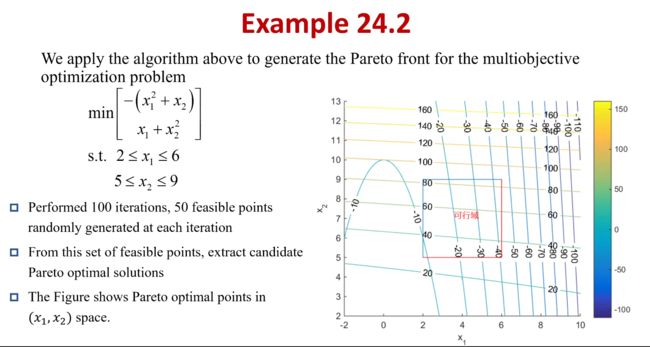
5.2 第二个实例

在求目标函数 $f_1,f_2$，的最小值的时候，当 A 与 B 相比 $f_1(x^{\ast })<f_1(\overline{x})$，且 $f_2(x^{\ast })<f_2(\overline{x})$ ，所以 B 不支配 A，而 A 支配 B， A 与 C 相比，$f_2(x)<f_2(x^{\ast })$，若 $f_1(x)<f_1(x^{\ast })$，则 C 支配 A，但是 $f_1(x)>f_1(x^{\ast })$,所以没有支配关系，属于非支配关系

分析可以知道，红色曲线上的点，在进行内部点之间比较的时候，如果一个点其中一个函数值小于另一个点对应的函数值时，那么此点的另一个函数值一定大于另一个对应的函数值

不同情况下的 Pareto 最优前沿

6. Pareto 算法

转化为单目标函数

将其中一个函数作为目标函数，其他函数作为约数条件

7. Pareto 的计算

7.1 第一个实例 ☆☆☆

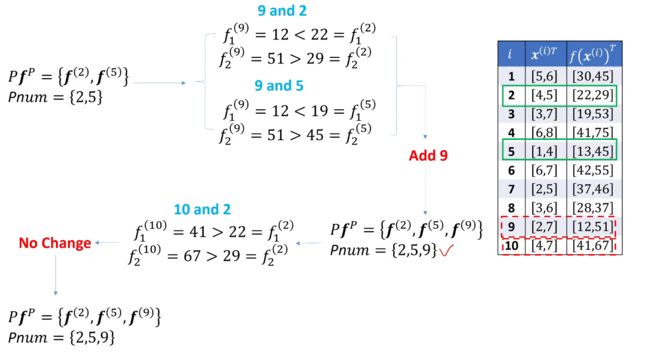
假设有两个目标目标函数，两个变量 $x_1,x_2$，对应的解集为 $f(x_1),f(x_2)$

1 号 与 2 号比，目标函数，2 号均比 1 号小，加入 pareto 点集， 3 号 和 2 号比，第一个目标函数小于 2 号，第二个目标函数大于 2 号，加入 pareto 点集

第 5 行数据再与 Pareto 候选集进行比较时，即 5 与 3 比较，发现 13 < 19 并且 45 < 53, 所以 3 被 5 支配，把 3 号点去掉，留下 5 号选入 Pareto 点集


最终的 pareto 前沿计算结果为：2， 9， 5

7.2 第二个实例

7.3 第三个实例

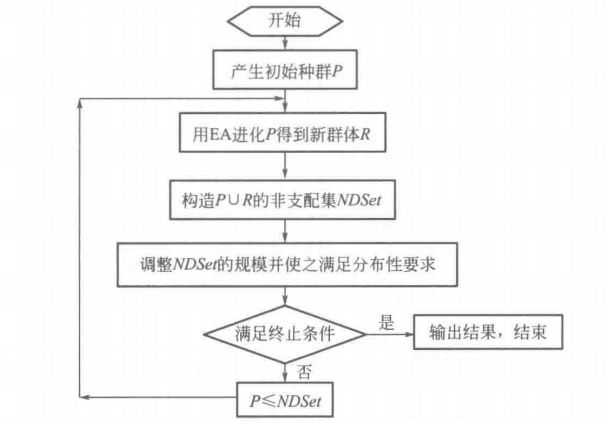
8. 基于 Pareto 的多目标进化算法的算法流程

首先产生一个初始种群 $P$，接着选择某个进化算法(如遗传算法)对 $P$ 执行进化操作(如交叉、变异和选择)，得到新的进化群体 $R$。然后采用某种策略构造 $P\cup R$ 的非支配集 $NDSet$，一般情况下在设计算法时已设置了非支配集的大小(如N),若当前非支配集 $NDSet$ 的大小大于或小于 $N$ 时，需要按照某种策略对 $NDSet$ 进行调整，调整时一方面使 $NDSet$ 满足大小要求，同时也必须使 $NDSet$ 满足分布性要求。之后判断是否满足终止条件，若满足终止条件则结束，否则将 $NDSet$ 中个体复制到 $P$ 中并继续下一轮进化。在设计MOEA时，一般用进化代数来控制算法的运行。