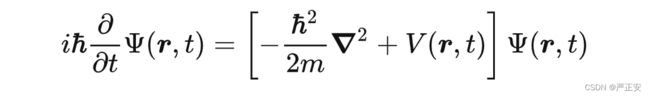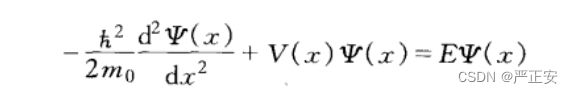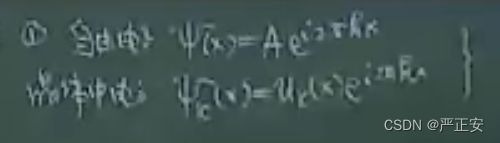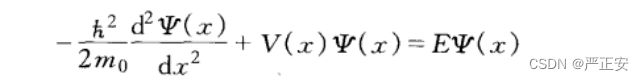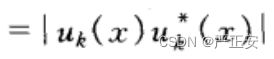半导体中的电子状态与能带

电子状态：电子的能量状态

微观粒子具有波粒二象性，经典物理用坐标和动量来描述，就波动性来说，我们用E（能量）和K（波数矢量）来描述微观粒子

半导体中的电子状态与能带

本书线索：（1）孤立原子的电子状态（氢原子（H）量子力学已经解决） 多电子

                  （2）空间自由电子的状态(普通物理学过)

                    半导体中的电子状态 -----> 电子的状态和特点

（1）原子中的电子状态：a. 单电子 首先是氢原子，En的表达式

                                          b.多电子 多电子及其电子的状态仍然不连续（用四个量子数来描述状态）

孤立原子核外的电子，其状态是一系列分立的能量确定值称为能级

（2）自由电子状态：考虑波动性的时候，考虑一维状态下的薛定谔方程

 设我们的势场是一个恒定常数==0，这样一来的话，把势场代入薛定谔方程就可以带入求解

解出波函数

由粒子性，电子的动量P, 能量E 

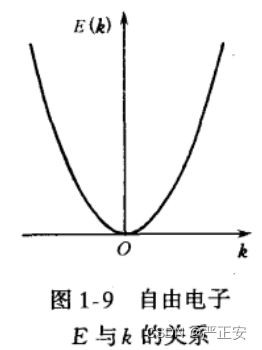
在恒定势场下，自由电子的EK关系，这个是一个连续的EK关系，因为你在求解自由电子的过程中是有解的，随着K的连续取值，所以E就是连续的

自由电子使其能量状态是连续的

（3）半导体中的电子状态与能带

        求解薛定谔方程，势场中的这一项需要确定，对于氢原子只有一个核外电子，势场只受原子核的作用，假设V（r）正比于（ 1/r ）

        势场是解决微观粒子波粒二象性的一个困难问题

        半导体当中的电子是在严格周期性重复排列的原子之间运动，势场形式复杂（忽略次要条件），所以就有各种各样的近似（就晶体来说有大量原子，同时也有大量电子），其中最成功的就是： 

1. 单电子近似 : 设电子是在严格周期性重复排列（晶体是没有缺陷的理想晶体）并且是固定不动（不随时间产生变化）的原子核势场以及大量电子的平均势场下运动，这就是所谓的单电子近似，有了单电子之后，就有了能带理论

意义：1. 单电子近似把晶体当中研究混合系统中的电子状态的问题分离出来 2.把众多电子相互牵制的复杂的多电子问题，近似成为对某一电子的作用，只是一个平均势场的作用

提出单电子近似是为了确定势场的形式

根据单电子近似：严格重复排列 : V（X）=V(X + Sa) S是整数，a是晶格常数

 周期性函数的种类很多，所以单电子近似只是给了一个势场的形式，解析式并没有出现

其中我们就可以构造各种各样的势场

布洛克证明了具有周期性势场的薛定谔方程，那么其解一定具有下面的形式，

把这样的波函数称作布洛克波函数

讨论一下解的形式：（1）自由电子来说

 形式上是相似的，他们都表示了波长为（1/k）沿着k方向传播的平面波，不同点在于晶体中电子的周期性调制振幅Uk（X）取代了自由电子的恒定振幅

(2)对于自由电子来说，波函数和波函数的共轭相乘 == A的平方（意义是考察对象在空间各点出现的概率），表明电子在空间各点等概率出现（各点出现的概率一样），既然是等概率出现，那么表示它是自由的，反映了电子在空间做自由运动

晶体中的电子，我们把布洛克函数和布洛克函数的共轭相乘，Uk（X），那么乘积还是周期性函数，说明晶体中找到该电子的概率具有周期性变化的性质，（电子不再属于某一个特定的原子而是可以从一个原子所谓的自由运动，运动到), 

半导体中的薛定谔方程以及薛定谔方程的解

---

布洛赫函数中的波矢k，具有量子数的作用，不同的k反映了不同的共有化运动状态

共有化运动就会形成能带

复习：

晶体中的薛定谔方程

 为了确定势场形式，就有了单电子近似（严格周期性排列，固定不动），我们可以确定晶体当中的势场是一个周期性势场，因为晶体是由组成晶体的原子周期性排列而成，

 沿着k方向传播的平面波，振幅是一个周期性振幅，有了布洛赫波函数以后，我们讨论了三件事情

1. 晶体当中电子所谓的布洛赫波函数与自由电子的波函数（自由电子是恒定振幅），形式上相似，不一样的地方在于，布洛赫是一个以周期性为 a 的调制振幅

2. 布洛赫波函数和它共轭的乘积，考察的是几率

 电子在晶体中出现的机率，不属于某一个特定的原子，而是以晶格常数a为周期

在晶胞对应点上，等几率出现，我们称为共有化运动

3.在布洛赫波函数中，波矢k具有量子数的作用，不同k反应不同的共有化运动状态

---

两种极端情况来说明电子的运动状态：

1.准自由电子近似  

  自由电子的运动状态时连续的，波矢k可以连续取值，所以能量是一个抛物线，也可以连续取值

  从自由电子的状态出发，设想将一个电子给它放入到晶体当中，由于晶格存在，电子在传播过程中给就会受到格点原子的反射（格点大量存在），大量反射存在，所以在一般情况下，各个反射波是会相互抵消的，对前进波无重大影响，但当满足布拉格反射条件的时候，就会形成驻波，所以我们把一般情况和特殊情况结合起来，综合上面 =》 其定态为驻波

我们以一维晶体为例，在一维晶体中，其布拉格反射条件，,

满足布拉格反射条件，这是一维条件下的满足形成驻波的反射条件，另外我们由量子力学理论，我们说电子的运动可以看作是波包的运动，并且波包的群速度就是电子运动的平均速度，设波爆的频率是,则电子运动的平均速度,   ,这是量子力学得到的结果，因为,两个式子联立一下，我们得到, 这个公式非常重要（电子运动的平均速度）在一维晶体情况下，,,那么在图上可以把点给标出来，原先的抛物线上，就有些点被标志出来，这些点满足布拉格条件，在满足，这些点就是驻点（波动中不动的点），，E,K关系的切线的斜率为0，由于形成的是驻波，所以电子的速度是0，所以曲线就要被扭曲了，在波矢，将会从连续的能量状态变成一系列能量允许和能量不允许相间隔的区间，那么我们把这样的能量允许的区间，称为允带，不允许出现的称为禁带。

这个就是我们所说的第一种极端的情况（准自由电子近似）

准束缚近似：从孤立原子核外电子的状态也就是能级出发

空间中孤立的原子核外电子的状态，形成了一系列确定的能量，把晶体看作是原子相互靠拢到一定程度的结果，晶体当中的电子，具有布洛赫波函数的性质，在晶胞对应电商等概率出现，共有化运动，（也就是说靠拢会出现电子的共有化运动），电子不再属于某一个特定的原子，作共有化运动的电子，不再长时间停留在某原子的一定状态中，而且只停留有限时间，那么我们根据测不准原理，（量子力学三个基本原理：测不准原理，能量量子化，泡利不相容原理），测不准原理说的是位置和动量这是一对测不准量，能量和具有这个能量的时间是一对测不准量，所以我们要用能量和波矢k来描述,电子属于这个原子，所以，晶体当中的电子，电子不再属于某一个特定的原子，, 不就是能级展宽成能带，我们刚才在准自由，当原子和原子相距的比较远的时候，我们把孤立原子相互靠拢，我们仍然可以用图来示意一下，横坐标原子间距，当原子间距比较大的时候，看作是孤立原子，看作形成孤立能级，随着靠拢，能级开始分裂，逐渐展宽成能带，也就是晶体当中原子核原子的实际距离，晶体中原子的距离,外层电子共有化运动来的早，所以展宽的大，内层电子展宽的小

晶体中电子的状态既不同于自由电子连续的E-K关系，也不同于孤立原子核外电子的状态（能级），而是形成了一系列想=相间隔的允带和禁带

（三） 布里渊区与能带

我们还是把刚才那个准自由电子就近似，如果是自由电子是抛物线型的，自由电子一旦进入晶体当中，在一些地方将会形成驻点，在这些地方束缚就是0，从连续的变成不连续的，使得切线的斜率为0，这么一个区间内，波矢的取值,，所谓布里渊区，就是把k的取值变一下，

在波矢  

在这些地方能量不连续，形成了一系列相间隔的允带和禁带，划分出了第一布里渊区，依次向左右，形成第二布里渊区.......

划分了布里渊区之后，禁带出现在处也就是布里渊区的界面上，

2.一个布里渊区对应于一个允带，周期性的函数给定特殊函数，薛定谔方程可以解决

在这个图的基础上，是原子周期性排列，所以晶体当中的E，K关系也应该周期话

第一布里渊区的曲线继续延续下去，所以晶体当中的势场是一个周期关系

3.晶体当中的E-K关系是周期性的，即

4.第一布里渊区又称为简约布里渊区，因为E~K关系是周期性的，所以只需要讨论布里渊区

（四）能带中的量子态数目

在能量允许的区间，波矢能否连续取值,一个允带中的取值方式和取值的数量

1. 要用到边界条件，一个允带对应一个布里渊区，为了简单一些，一维晶体中，用所谓的循环边界条件（首尾相连）（波恩-卡曼边界条件）,布洛赫波函数,其中这个l，在一维情况下，线状的晶体，如果是由N个原子组成，那么应该是N和a的乘积，称为循环边界条件

,那么在这个式子里面，晶体首尾相连，是循环的=1,也就是都是满足的，这样以来，,如果是三维，,,波矢K的取值并不连续，而且波矢K的取值,在K空间是均匀分布的，在一个能量允许的区间内部，还有好多好多的能级是取不到的

一个布里渊区的长度,一个允许的K值所占的长度=，，所以K的取值应该等于,每个布里渊区也就是一个能带，共有N个K的取值，他们均匀分布在K空间，每一个允许的K值对应了一个能量状态，每个能级至多包含两个自旋相反的电子，因为每一个能级上可以容纳自旋相反的两个电子，所以每一个允带中，最多可以容纳两倍N个电子，N是晶体的固体物理学原胞数，也就是总原子数

1.原胞: 只反映周期性而不反应各种对称性，一个原胞平均包含一个格点

2.每个允带中电子的能量也是不连续的，允带是由许多密集的能级组成的，因此是近似连续的（称为准连续），如果我们想计算一下在这样的一个允带中有多少电子，如果认为能量是连续的

4.导体，半导体和绝缘体的能带

晶体当中的电子状态一系列允许和不允许的区间，下面就想用能带的说法，来说明为什么有些是绝缘体，导体还有半导体？

固体物理认为，电子能够导电，在外电场作用下，其电子的能量状态和分布情况发生改变

满带中的电子在外电场作用下不参与导电

什么是满带？

所有的能级（从低到高）都被自旋相反的电子占据了，在这样的一个所有能级都被自旋相反的电子填充，如果我们加一个电场的话，看电子的运动情况

电子在力的作用下位移，电子能量的变化等于电场力对电子所做的功，

波矢K对时间的变化率为定值电子从A‘流出填入A，在满带作用下，电子运动的结果，没有改变电子的状态

a. 因为电子的运动没有改变能量状态和布里渊区内的分布情况，因此满带电子不导电

b. 与之对应的是第二种情况，半满带中的电子，在外电场的作用下，可以导电

在半满带中如果有外电场E的化，也会在K空间作匀速运动，运动的结果左边的能量高，右边的能量低，既改变了能量状态也改变了布里渊区内的分布情况，满带当中的电子和半满带中的电子，两个的结果不一样

想象两个瓶子，一个装满水，另一个装了半瓶水

内层电子占据的都是满带，所以内层电子对导电没有贡献

c. 导体，半导体，绝缘体的能带

导体一定存在半满带

绝缘体的能带和T=0K时半导体能带是相似的

绝缘体的禁带宽度：绝缘体的禁带宽度比较大，=（6~7ev），而半导体的禁带宽度通常在1ev左右，例如300K下，Si的Eg 1.12ev，Ge 0.67ev，GaAs 1.43ev,当外界条件变化的时候，里面的电子会获得能量，获得能量之后，满带中少量电子，跃迁到上一个空带的底部附近，所以满带中的电子和原先空带中的少量电子都参与导电，所以常温下具有一定的导电能力，通常把满带中，少量电子跃迁后，剩余的大量电子对电流的贡献，用少量的带正电的准粒子加以等效描述，称为空穴