栈、队列、优先级队列的模拟实现
栈、队列、优先级队列
栈没有了迭代器,他不是容器了,他是一个容器适配器。
我们学习它的操作完全可以效仿我们string,vector,list
一、栈的模拟实现
既然我们大家都会用vector和list了,为什们不拿已有的容器封装,让我们的栈更加简单,就是我们常说的适配器模式。
用list和用vector都可以,所以我们用类模板的时候加一个参数,表示我们用哪个容器。一会我们还会加默认参数让我们的栈更加完美。
//适配器模式/配接器
template<class T,class Container>
class stack
{
private:
Container _con;
};
① 模拟栈的代码
我们用模拟栈,是不是非常简单,就是我们之前的东西
//适配器模式/配接器
template<class T,class Container =vector<T> >
class stack
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
const T& top()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
②测试模拟栈
我们传栈的参数的时候,我们传可以用vector,list。这取决于我们传的参数。也可以不传用缺省参数。
void test_stack()
{
//数组栈
stack<int, vector<int>> st;
//链式栈
stack<int, list<int>> st;
//用缺省参数
stack<int> st;
st.push(1);
st.push(2);
st.push(3);
st.push(4);
while (!st.empty())
{
cout << st.top() << " ";
st.pop();
}
cout << endl;
}
二、队列的模拟实现
有了栈的前车,我们造后车,那不就是小菜一碟吗?
① 队列模拟实现的代码
对于队列,不太适合vector,对于头删的功能,效率太低。
一般用list,所以我们的默认参数用list
template<class T, class Container = list<T> >
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
const T& front()
{
return _con.front();
}
const T& back()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
②测设模拟队列
直接用默认参数就可以了。
void test_queue()
{
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
}
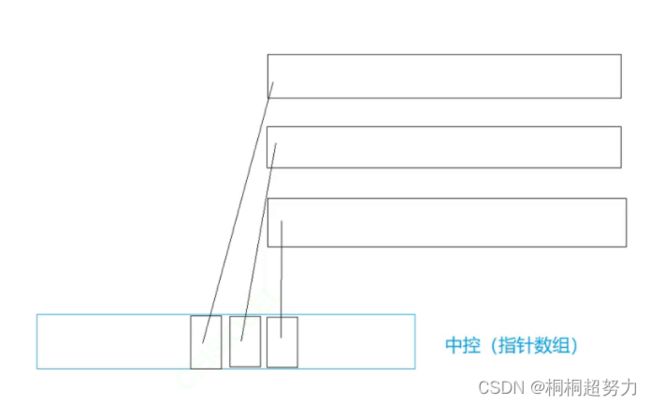
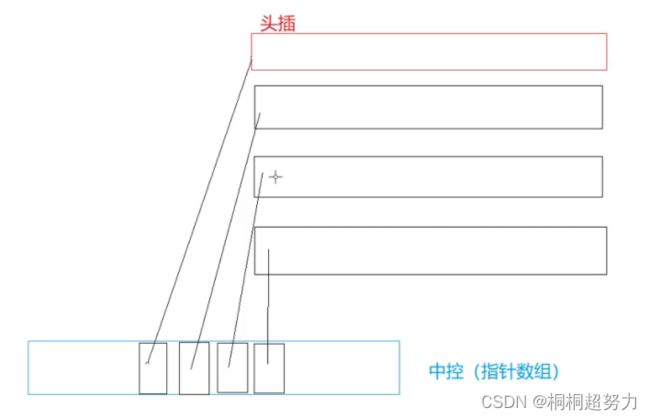
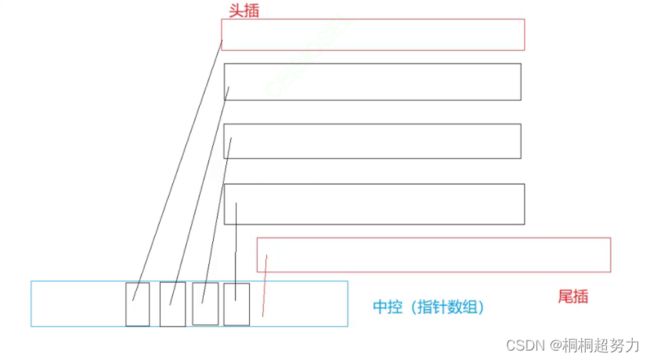
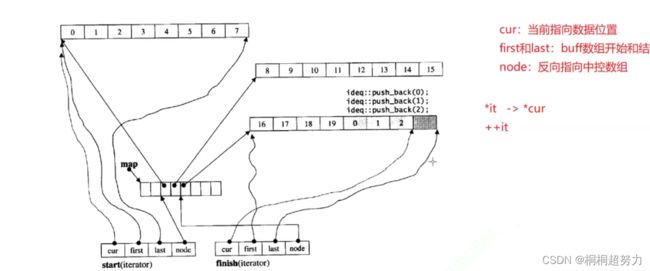
三、deque容器(栈和队列的适配器)
deque就是vector和list的结合体。作为队列的默认容器参数
即支持vector的功能也支持list的功能。
对于扩容问题,就是我们中控满了,就扩容,但是扩容代价低。
-
优点
-
- 相比vector,扩容的代价低
-
- 头插头删,尾插尾删的效率比vector高
-
- 支持的随机访问
缺点
-
- 中间的插入删除很难做
-
- 没有vector和list优点极致。
四、优先级队列priority_queue
它的默认容器时vector.
类似于我们的堆。
出队列就是优先级高的先出。
默认时大堆,大的优先级高。所以出队列大的先出,就会是降序。
但是如果我们想让变成升序,我们就要用我们的仿函数。看我们的测试优先级队列
① 优先级队列的使用
void test_priority_queue()
{
priority_queue<int> pq;
pq.push(1);
pq.push(2);
pq.push(3);
pq.push(4);
pq.push(4);
pq.push(15);
//这些适配器没有迭代器,遍历不可以用迭代器
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
将其变成升序。优先级变一下。变成小的优先级高。就要用仿函数。
void test_priority_queue()
{
//第三个模板参数就是我们的访函数
//小堆--小的优先级高
priority_queue<int,vector<int>,greater<int>> pq;
pq.push(1);
pq.push(2);
pq.push(3);
pq.push(4);
pq.push(4);
pq.push(15);
//这些适配器没有迭代器,遍历不可以用迭代器
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
②模拟实现优先级队列(大堆)
跟栈和队列一样,都是用容器适配器,其功能参考我们的堆。优先级队列的插入和删除和堆是一样的。
template<class T, class Container = vector<T>>
class priority_queue
{
public:
void AdjustDown(T parent)
{
int child = (parent * 2) + 1;
while (child < _con.size())
{
if (child + 1 < _con.size() && _con[child + 1] > _con[child])
{
child++;
}
if (_con[parent] < _con[child])
{
std::swap(_con[parent], _con[child]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;
}
}
}
void AdjustUp( T child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_con[child] > _con[parent])
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void push(const T& x)
{
_con.push_back(x);
AdjustUp(_con.size()-1);
}
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
AdjustDown( 0);
}
bool empty()
{
return _con.empty();
}
T& top()
{
return _con[0];
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
③测试模拟优先级队列
void test_priority_quene()
{
priority_queue<int,deque<int>> pq;
pq.push(1);
pq.push(2);
pq.push(3);
pq.push(4);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
④访函数
-
为什们要有仿函数?
-
我们不想让大的优先级高。
现在想让小的数优先级高,建立一个小堆。
其实就是改变大于小于符号就可以,但是我们难道再写一个类,改变大于小于号吗?
C++不会这么告,会在模板参数用仿函数实现这个功能。
仿函数就是重载了一个符号
(),能够像函数一样使用,我们用它就是为了解决函数指针难懂的问题。
Ⅰ两种仿函数
仿函数一般使用struct使他的权限公开,在优先级队列中能够访问它。
less, 使大的数优先级高。建大堆的时候用less,输出成升序。
template <class T>
struct less
{
bool operator()(cosnt T& x, const T& y)
{
return x < y;
}
};
greater使小的优先级高。建小堆的时候用greater,输出成降序。
template<class T>
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
Ⅱ优先级队列中加入仿函数
先建立大堆,用
less仿函数
less和greater类
template<class T>
struct less
{
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
template<class T>
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
在向上和向下调整函数中,用它
//增加一个模板参数
template<class T, class Container = vector<T> ,class Comapre = less<T>>
class priority_queue
{
public:
void AdjustDown(T parent)
{
//实例化
Comapre com;
int child = (parent * 2) + 1;
while (child < _con.size())
{
//if (child + 1 < _con.size() && _con[child + 1] > _con[child])
if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
{
child++;
}
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
std::swap(_con[parent], _con[child]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;
}
}
}
void AdjustUp( T child)
{
Comapre com;
int parent = (child - 1) / 2;
while (child > 0)
{
//if (_con[child] > _con[parent])
if (com(_con[parent], _con[child]))
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void push(const T& x)
{
_con.push_back(x);
AdjustUp(_con.size()-1);
}
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
AdjustDown( (_con.size() - 1 - 1) / 2);
}
bool empty()
{
return _con.empty();
}
T& top()
{
return _con[0];
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
栈的Oj题
①最小栈
思路:常数时间,就是时间复杂度就是O(1)
我们不能遍历栈,遍历栈的时间复杂度就是O(n)
我们建立两个栈,一个正常的插入删除,另一个存放比自己栈顶小于等于的值,为了我们删除栈的时候跟新最小值。
class MinStack {
public:
MinStack() {
}
void push(int val) {
st.push(val);
if(!minst.empty())
{
if(minst.top()>=val)
{
minst.push(val);
}
}
else
{
minst.push(val);
}
}
void pop() {
if(!st.empty())
{
int top = st.top();
st.pop();
if(top==minst.top())
{
minst.pop();
}
}
}
int top() {
int top = st.top();
return top;
}
int getMin() {
int min = minst.top();
return min;
}
stack<int> st;
stack<int> minst;
};
②栈的压入、弹出序列
思路就是用一个栈模拟栈的压入和弹出
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
int pushi=0;
int popi=0;
while(pushi<pushV.size())
{
st.push(pushV[pushi++]);
while(!st.empty()&&st.top()==popV[popi])
{
st.pop();
popi++;
}
}
if(st.empty())
{
return true;
}
else
{
return false;
}
}
stack<int> st;
};
③逆波兰表达式求值
这个逆波兰表达式,已经按照运算符的优先级排好了,只需要用栈,编译器就可以很好的进行运算。
用栈的方法
1.遇到数字,我们就入栈。
2.遇到操作符,我们去栈顶的两个操作数进行运算,栈顶的第一个操作数是右操作数,第二个操作数是左操作数。运算结果重新入栈
最后栈中的值就是我们最后的结果。
class Solution {
public:
int evalRPN(vector<string>& tokens) {
int ret = 0;
for(auto a:tokens)
{
if(a=="+"||a=="-"||a=="*"||a=="/")
{
int right = st.top();
st.pop();
int left =st.top();
st.pop();
//switch必须是整型
switch(a[0])
{
case '+':
ret = left+right;
st.push(ret);
break;
case '-':
ret = left-right;
st.push(ret);
break;
case '*':
ret = left*right;
st.push(ret);
break;
case '/':
ret = left/right;
st.push(ret);
break;
}
}
else
{
//有字符串转数字的函数
st.push(stoi(a));
}
}
int top = st.top();
return top;
}
stack<int> st;
};
方法:从左向右走
1.遇到操作数输出
2.操作符
a.栈为空,进栈
b.栈不为空,跟栈顶操作符比较,
比栈顶的操作符优先级高,进栈,然后进行第一步操作,取下一个。
比栈顶操作符优先级低或相等,出栈顶的操作符输出。然后进行b操作。
最后结束将栈的操作符输出。
举个例子:
1 + 2 * 3 - 4
我们的栈为st。
输出的后缀用我们想要的容器接受。
先遇到操作数
1,输出到后缀的容器。
然后遇到操作符+,进栈。
遇到操作数2,输出到后缀的容器中
遇到操作符*,跟栈顶的元素+,比较优先级高,我们入栈。
再遇到操作数3,输出到后缀的容器中。
遇到操作符-,跟栈顶元素*比较,优先级低,出栈顶元素*进入后缀的容器。
然后操作符-再和栈顶元素+,比较,优先级相同,出栈顶元素-进入后缀的容器中。
这时栈为空,-进栈。
然后遇到操作数4,输出到后缀的容器。
然后将栈的操作符输出。
最后后缀的容器为1 2 3 * + 4 -.
我们有了后缀,就可以用代码去走了。像我们上面那样。
如果有括号就比我们之前难处理多了
1.()优先级最低
2.(不参与比较直接入栈
3.)参与比较,直接遇到(