AVL树大讲堂
1.基础概念介绍
首先在前面我们介绍了二叉搜索树,但是如果当存储的数据接近有序或者恰巧有序的时候,二叉搜索树将逐渐退化为单支树,导致搜索效率降低,因此我们的avl树便为了解决这一问题而诞生了。
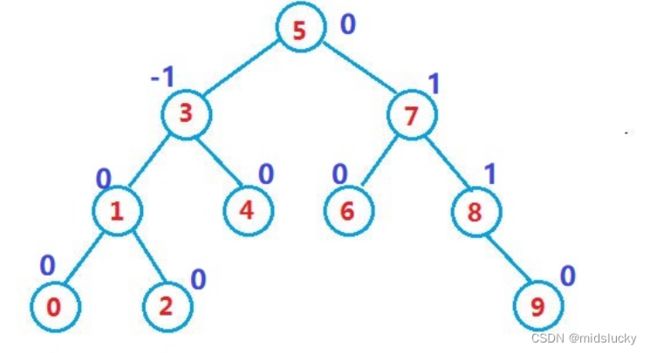
基础性质:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(右子树的高度减去左子树的高度),即可降低树的高度,从而减少平均搜索长度。
如图所示便是一棵典型的AVL树:
2.基础代码的复现
2.1基础结点
template<K,V>
class AVLTreeNode
{
AVLTreeNode<K,V>* _left;
AVLTreeNode<K,V>* _right;
AVLTreeNode<K,V>* _parent;
pair<K,V> _kv;
int _bf; //平衡因子
AVLTreeNode(const pair<K,V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};
2.2树内部的基础封装
template<k,v>
class AVLTree
{
typedef AVLTreeNode<k,v> Node;
AVLTree()
:_root(nullptr)
{}
private:
Node* _root;
}
2.3最麻烦的插入(此处先搭一个板子我们分两大部分进行讲解)
首先我们在这边先讲解一下大致思路。结合上面的代码我们可以看到相对比于普通的二叉搜索树而言,其结点中多了一个父结点的指针和一个平衡因子,而其本质上来说插入结点的规则要和二叉搜索树保持一致,那么这样思路便简单不少。首先我们先要保证其具备搜索二叉树的特性,其次每插入一个新的结点难免会造成平衡因子的变化,所以我们需要时时注意那些会发生改变的平衡因子,为此我们便需要写一个平衡因子的检查功能,并当平衡因子超过大于1或者小于-1时,采取相应措施,使其回归正常值。
实际代码:
Insert(const pair<K,V>& kv)
{
if(_root == nullptr)
{
Node* newnode = new Node(_kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while(cur)
{
if(cur->_kv.first > kv.first)//注意这边给的值是pair,所以比较的时候需要这么写
{
parent = cur;
cur = cur->_left;
}
if(cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(kv); //注意此处我直接用cur开,而没有在开一个新结点,省掉了cur的处理
cur->_parent = parent;
if(parent->_kv.first > kv.first)
{
parent->left = cur;
cur->_parent = parent;
}
else if
{
parent->riget = cur;
cur->_parent = parent;
}
//到此处我们的插入就完成了
//接下来我们需要开始控制平衡
while(parent)
{
if (cur == parent->_left)
parent->_bf--;
else
parent->_bf++;
if(parent->_bf == 0) { break;}
else if(parent->_bf == 1 || parent->_bf == -1)
{
//这个时候明显会影响上面结点的平衡因子,所以需要往上找
cur = parent;
parent = parent->_parent;
}
else if(parent->_bf == 2 || parent->_bf == -2)//开始旋转处理
{
if (parent->_bf == -2 && cur->_bf == -1)//右单旋
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)//左右双旋
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)//右左双旋
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
// 说明插入更新平衡因子之前,树中平衡因子就有问题了
assert(false);
}
}
return true;
}
当然这有几个函数的代码这里没给,先不急我们先分析一下其原理。
3. 4种旋转的原理分析
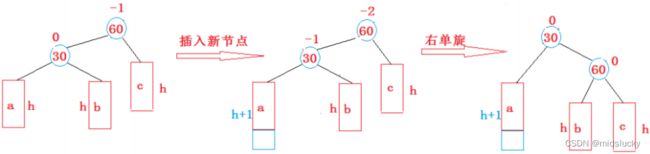
1.右单旋
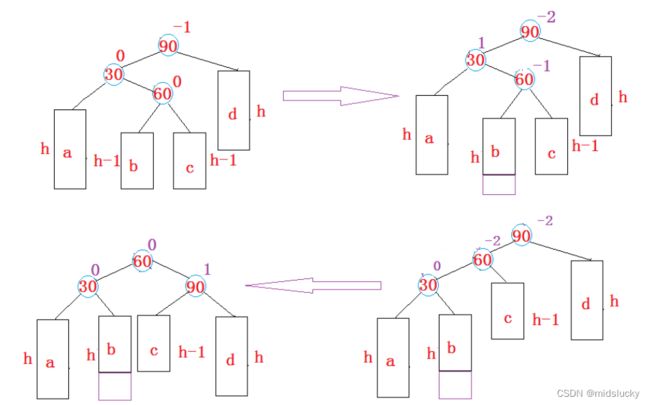
2.左右单旋
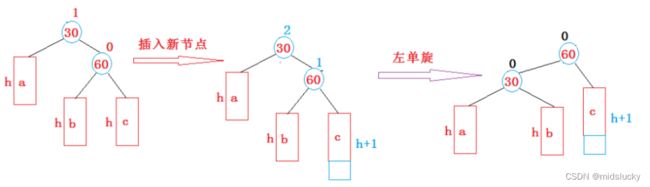
3.左单旋
4.右左单旋
ok仔细观察4幅图片可以很清晰的观察到整个过程**(看这段话之前请花时间多看看,拿1.2两幅图相对比,在拿3.4两幅图相对比)**
当然可以看出1.3两幅图最后插入的一个数都是插在了靠边的那棵子树,因此一次旋转后就能解决,而2.4是插在了靠边那棵子树的傍边,所以变有了一下的情况,而这4种情况可以说是囊括了所有的可能性。
4.个旋转的代码实现
1.右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
parentParent->_left = subL;
else
parentParent->_right = subL;
subL->_parent = parentParent;
}
subL->_bf = parent->_bf = 0;
}
2.左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
parentParent->_left = subR;
else
parentParent->_right = subR;
subR->_parent = parentParent;
}
subR->_bf = parent->_bf = 0;
}
3.左右双旋
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
4.右左双旋
void RotateRL(Node* parent)
{
RotateR(parent->_right);
RotateL(parent);
}